1 球坐标系下的三重积分
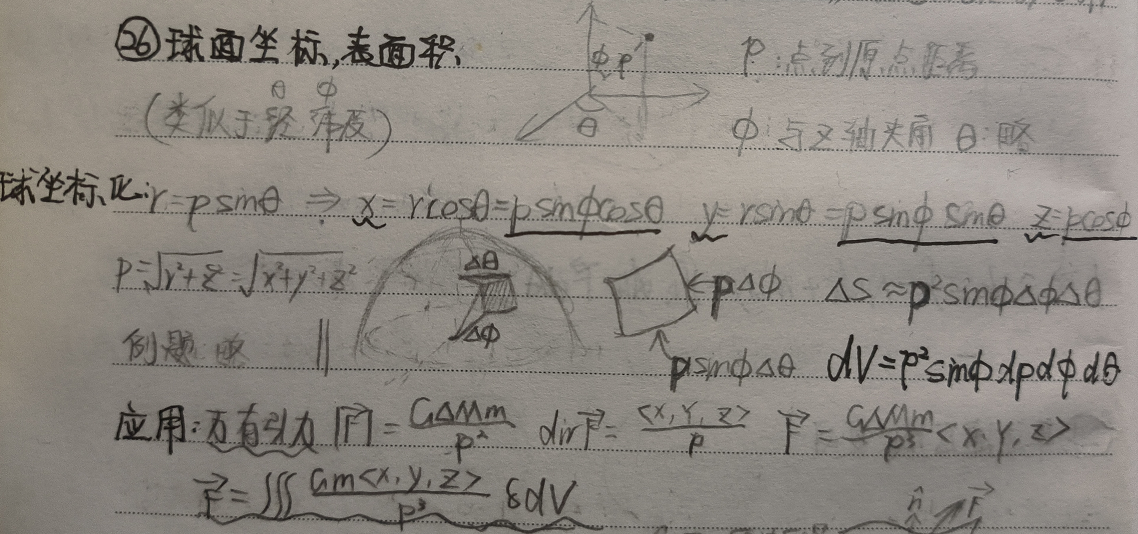
球坐标系是三维坐标系的一种,以坐标原点为参考点,点$P$的坐标由方位角$\theta$(线$OP$投影到$xy$平面后与$x$轴的夹角)、仰角$\phi$(线$OP$与$z$轴的夹角)和距离$\rho$(点到原点的距离)构成。经纬度就是球坐标系的一种常见形式,其中$\theta$与经度相似,$\phi$与维度相似。
球坐标化通过以下公式实现从$(x,y,z)$到$(\rho,\phi,\theta)$的转化: $$\begin{equation} \left\{ \begin{gathered} r=\rho sin\theta \ \\ x=rcos\theta=\rho sin\phi cos\theta \ \\ y=rsin\theta=\rho sin\phi sin\theta \ \\ z=\rho cos\phi \ \\ \rho=\sqrt{r^2+z^2}=\sqrt{x^2+y^2+z^2} \end{gathered} \right. \end{equation}$$
不难发现,直角坐标系会先进行柱坐标化,再实现的球坐标化
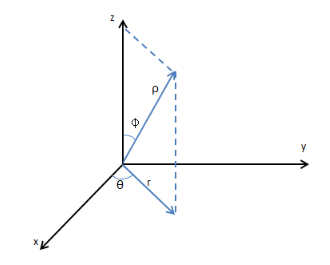
如上图所示,当$\Delta \phi$和$\Delta \theta$产生很小变化时,对应的面积变化$\Delta S$: $$\Delta S=p\cdot q\approx a\Delta \phi\cdot asin\phi \Delta\theta=a^2sin\phi \Delta \phi \Delta\theta$$ 将距离$a$替换为$rho$,由此可得球坐标系下三重积分的体积积元$dV$: $$dV=\rho^2 sin\phi d\rho d\phi d\theta$$
2 球坐标系下的三重积分示例
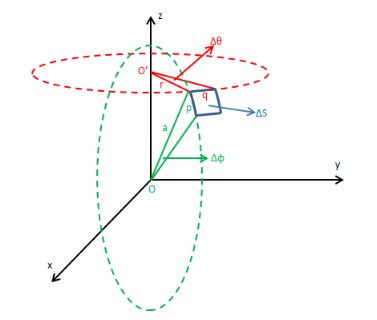
计算单位球和$z = 2^{-\frac{1}{2}}$所围的区域的体积:
易判断$\theta$的取值范围在$[0,2\pi]$,$\phi$的取值范围在$[0,\frac{\pi}{4}]$

由上图可知,$\rho$的最大取值为1,最小取值受到$\phi$的制约。当$\phi$等于0时,$\rho$的最小取值为$\frac{\sqrt{2}}{2}$;当$\phi$大于0时,$\rho$的最小取值为$\frac{\sqrt{2}}{2}sec\phi$。所以本示例最终计算过程如下: $$\int \! \! \! \int \! \! \! \int dV=\int \! \! \! \int \! \! \! \int \rho^2 sin\phi d\rho d\phi d\theta = \int_0^{2\pi}\int_0^{\frac{\pi}{4}} \int_{\frac{\sqrt{2}}{2}sec\phi}^1 \rho^2 sin\phi d\rho d\phi d\theta$$
3 球坐标系下的三重积分应用
已知原点位置存在固定的物体$A$,其质量为$m$,在$(x,y,z)$处存在另一个物体$B$,其在此位置的局部质量为$\Delta M$,根据万有引力定理可知,引力的大小和方向分别为: $$|F|=\frac{G\Delta Mm}{\rho^2},dir(\vec{F})=\frac{<x,y,z>}{\rho}$$ 对于物体$B$来说,其在某点的局部质量是由局部体积和密度决定的:$\Delta M=\delta \Delta V$
所以两物体间的万有引力可以通过以下三重积分进行求解: $$\vec{F}=\int \! \! \! \int \! \! \! \int_R\frac{Gm}{\rho^3}<x,y,z> \delta dV$$ 同理,也可以只求解万有引力沿$z$轴方向的结果: $$\vec{F_z}=\int \! \! \! \int \! \! \! \int_R\frac{Gmz}{\rho^3}\delta dV$$
4 参考