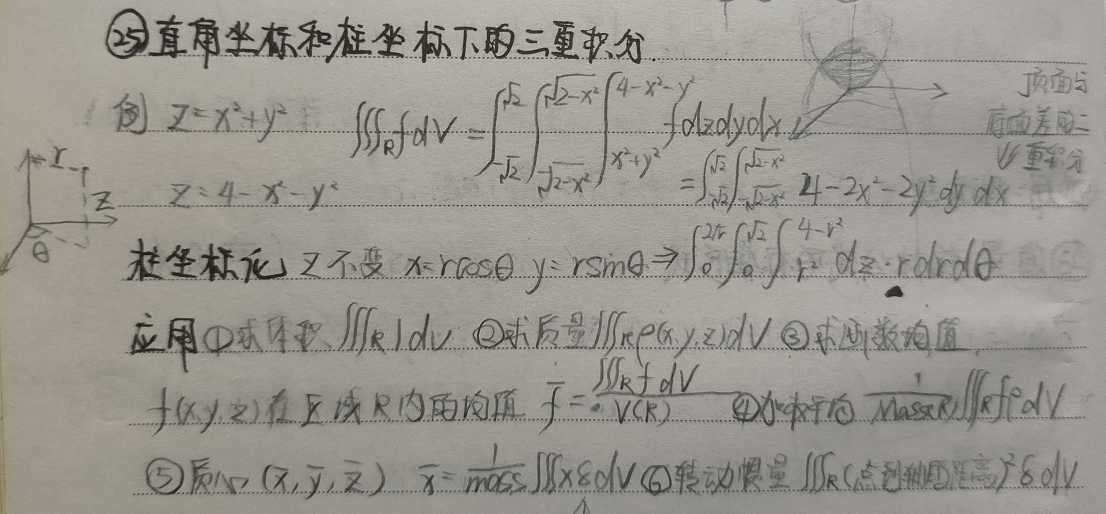1 直角坐标系下的三重积分
二重积分的几何意义是面积,三重积分的几何意义是体积,二者的计算也是可以类推的
举例:计算两个曲面$z = x^2+y^2$和$z = 4–x^2–y^2$围成的图形的体积
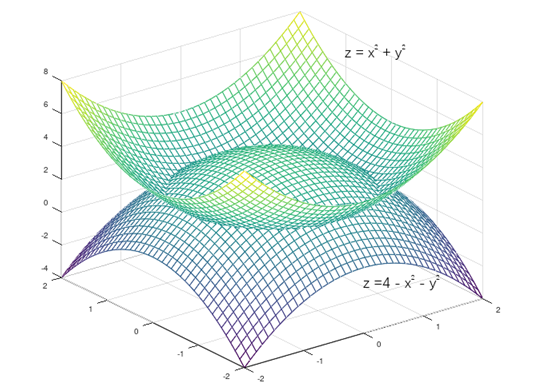
根据$x^2 + y^2\leq 4 – x^2 – y^2$推得$x,y$的限制条件:$x^2+y^2\leq 2$
将限制条件转化为积分上下限,可得以下计算公式: $$\int \! \! \! \int \! \! \! \int_R fdV=\int_{-\sqrt{2}}^{\sqrt{2}}\int_{-\sqrt{2-x^2}}^{\sqrt{2-x^2}}\int_{x^2+y^2}^{4-x^2-y^2}1dzdydx$$ 剩余计算过程,略
2 柱坐标系下的三重积分
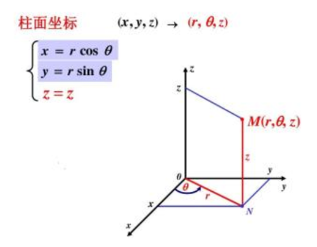
柱坐标化其实是一种三维直角坐标系版的“极坐标化”:
$$x=rcos\theta, y=rsin\theta,z=z$$
所以上一节中的示例柱坐标化后的结果如下: $$\int_{-\sqrt{2}}^{\sqrt{2}}\int_{-\sqrt{2-x^2}}^{\sqrt{2-x^2}}\int_{x^2+y^2}^{4-x^2-y^2}dzdydx=\int_{0}^{2\pi}\int_{0}^{\sqrt{2}}\int_{r^2}^{4-r^2}dzdrd\theta$$
3 三重积分的常见应用
- 计算体积:$V=\int !!! \int !!! \int_R 1dV$
- 计算质量:$M=\int !!! \int !!! \int_R \rho(x,y,z) dV$
- 求函数均值:$\overline{f}=\frac{\int !!! \int !!! \int_R f dV}{V}$
- 求加权平均:$\overline{f}_{weight}=\frac{\int !!! \int !!! \int_R f \rho(x,y,z) dV}{M}$
- 计算质心$(\overline{x},\overline{y},\overline{z})$:$\overline{x}==\frac{\int !!! \int !!! \int_R x \rho(x,y,z) dV}{M}$
- 求转动惯量:$I=\int !!! \int !!! \int_R (点到转轴的距离)^2\rho(x,y,z) dV$
4 参考