1 通量的计算公式及证明
前情回顾:
- 上一节提出了通量的计算(面积分):$Flux=\int !!! \int _S\vec{F}\hat{n}dS$
- 示例1针对曲面法向量与向量场平行的特殊情况进行了计算过程展示
- 示例2通过球坐标化的方法,先进行参数的变换,再进行后续的计算
以上的两种示例都属于现实中的特殊情况,本节课程则提出了更为通用的计算方法: $$Flux=\int \! \! \! \int _S\vec{F}\hat{n}dS=\pm \int \! \! \! \int _S\vec{F}\cdot <-f_x,-f_y,1>dxdy$$
以上公式成立的核心在于证明$\hat{n}dS=\pm <-f_x,-f_y,1>dxdy$
证明过程:
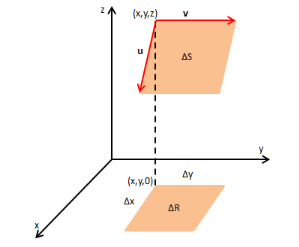
- 假设曲面$S$上的面积元是$\Delta S$,以其中一个顶点$(x,y,z)$出发,可得到向量$\vec{U}$和$\vec{V}$
- $\Delta S$面积的向量表达形式如下:$\hat{n}\Delta S=\Delta\vec{S}=\pm \vec{U}\times \vec{V}$ (叉乘结果的几何意义是面积)
- 设$z=f(x,y)$,假设面积元$\Delta S$投影到$x$轴的变化为$\Delta x$,投影到$y$轴的变化为$\Delta y$
- 则$\Delta x$引起的$z$轴变化为$\Delta z=f(x+\Delta x,y)-f(x,y)\approx f_x\Delta x$,同理$\Delta y$引起的$z$轴变化为$\Delta z=f(x,y+\Delta y)-f(x,y)\approx f_y\Delta y$
- 由此可得$\vec{U}\approx <\Delta x,0,f_x\Delta x>$,$\vec{V}\approx <0,\Delta y,f_y\Delta y>$
- 综合以上信息,最终可证明通量计算公式:
$$\Delta\vec{S}=\pm \vec{U}\times \vec{V}= \left| \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 0 & f_x \\ 1 & 0 & f_x \\ \end{matrix} \right|\Delta x \Delta y=<-f_x,-f_y,1>\Delta x\Delta y$$
2 通量的计算公式的拓展
拓展1:根据此公式,还容易可推得法向量$\hat{n}$和面积元$\Delta{S}$的计算公式: $$\begin{equation} \left\{ \begin{gathered} \hat{n}=dir(d\vec{S})=\frac{<-f_x,-f_y,1>}{\sqrt{<f_x^2+f_y^2+1>}} \ \\ \Delta{S}=|d\vec{S}|=\sqrt{<f_x^2+f_y^2+1>}dxdy \end{gathered} \right. \end{equation}$$
拓展2:通量的计算公式还可以拓展到参数方程的形式中
假设$x=x(u,v),y=y(u,v),z=z(u,v),<x,y,z>=\vec{r}=\vec{r}(u,v)$
类似于上一节的证明过程,$\vec{r}(u+\Delta u,v)-\vec{r}(u,v)\approx (\partial{\vec{r}}/\partial{u})\Delta u$,$\vec{r}(u,v+\Delta v)-\vec{r}(u,v)\approx (\partial{\vec{r}}/\partial{v})\Delta v$。此时通量的计算公式如下: $$\hat{n}dS=\pm (\partial{\vec{r}}/\partial{u})\Delta u\times (\partial{\vec{r}}/\partial{v})\Delta v$$ 拓展3:在曲面法向量已知的情况下,可以简化通量的计算公式
假设面积元$\Delta S$在$xy$平面上的投影是$\Delta A$,则$\Delta A=\Delta S\times cos\alpha=\Delta S\times \frac{\vec{N}\cdot \vec{k}}{|\vec{N}|}$。其中$\alpha$表示为$\Delta S$与$\Delta A$的夹角,$\vec{k}$为垂直的单位向量$<0,0,1>$。此时通量的计算公式如下: $$\hat{n}dS=\frac{\vec{N}\cdot \vec{k}}{|\vec{N}|}dA=\frac{\vec{N}\cdot \vec{k}}{|\vec{N}|}dxdy$$
3 散度定理
又称为高斯-格林(Gauss-Green)定理,是三维空间中通量计算的格林公式
假设闭合曲面$S$包含的空间为$D$,$\hat{n}$表示曲面的法方向(指向空间外侧),而空间向量场$\vec{F}$在空间$D$中处处可微,则曲面$S$的通量等于散度在空间$D$上的体积积分: $$∯_S\vec{F}\cdot d\vec{S}=\int \! \! \!\int \! \! \!\int_D dir(\vec{F})dV$$ 其中$dir$表示散度计算:$div(P\hat{i}+Q\hat{j}+R\hat{k})=P_x+Q_y+R_z$
关于散度定理的证明和应用,将在下一课时进行具体讲解
4 参考
