1 判断梯度场
上一节对于向量场判断是否为梯度场已有较为全面的表述
本小节将从梯度场的性质出发,展示最常见且便捷的判断方法
如果$\vec{F}$是梯度场,则$\vec{F}=\nabla f,M=f_x,N=f_y$
由$f_{xy}=f_{yx}$可知,梯度场$\vec{F}$需要满足:$M_y=N_x$
- $\vec{F}$是梯度场,是$M_y=N_x$的充分不必要条件
- $M_y=N_x$在$\vec{F}$处处有定义可导的前提下,可推得$\vec{F}$是梯度场
- 在后续的第24节课中将提及,这一前提是在限定$\vec{F}$定义域为单连通区域
以上一课时的第三小节例题说明:$\vec{F}=<-y,x>$
$M=-y,N=x$,由于$M_y\neq N_x$,势函数不存在,所以$\vec{F}$不是梯度场
2 寻找势函数
寻找势函数的前提是$M_y=N_x$
方法一:计算线积分
易知$\int_c \vec{F}\cdot d\vec{r}=f(x,y)-f(0,0)$,所以$f(x,y)=\int_c \vec{F}\cdot d\vec{r}+f(0,0)$
考虑到梯度场路径独立的性质,路径$c$可拆分成路径$c_1$和路径$c_2$:
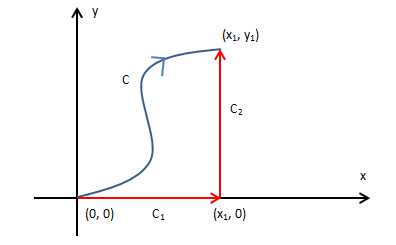
所以$f(x,y)=\int_{c_1} \vec{F}\cdot d\vec{r}+\int_{c_2} \vec{F}\cdot d\vec{r}+f(0,0)$
- 计算路径$c_1$时,$y=0,dy=0,0\leq x\leq x_1$
- 计算路径$c_2$时,$x=x_1,dx=0,0\leq y\leq y_1$
- 借助路径独立的性质,计算过程得到了极大简化
方法二:求不定积分
势函数满足以下形式:$\int(f_x)dx=F^{\ast}(x)+g(y),\int(f_y)dx=F^{\ast}(y)+g(x)$
所以可以先根据$f_x=M(x,y)$还原势函数中包含$x$的部分$F^{\ast}(x)$,保留仅包含$y$的未知部分为$g(y)$,再考虑根据$f_y=N(x,y)$还原势函数中仅包含$y$的未知部分$g(y)$
此方法较难描述,可参考下一节的示例进行直观理解
3 寻找势函数的示例
例题:求解梯度场$\vec{F}=<4x^2+8xy,3y^2+4x^2>$的势函数
方法一(计算线积分): $$\begin{align} f(x,y) & = \int_{c_1} \vec{F}\cdot d\vec{r}+\int_{c_2} \vec{F}\cdot d\vec{r}+f(0,0) \ \\ & = \int_0^{x_1} (4x^2+8x\cdot 0)\cdot dx+\int_0^{y_1} (3y^2+4x_1^2)dy+f(0,0) \ \\ & = \frac{4}{3}x_1^3+y_1^3+4x_1^2y_1+C \end{align} $$ 方法二(求不定积分):
$$ \begin{align} \int(f_x)dx & = F^{\ast}(x)+g(y) \ \\ & = \frac{4}{3}x^3+4x^2y+g(y) \end{align}$$ $$\therefore f_y=3y^2+4x^2=4x^2+g'(y),g(y)=y^3+C$$ $$\therefore f(x,y) = \frac{4}{3}x^3+y^3+4x^2y+C$$
相比较来说,方法二更为简单常用 对于非线性复杂梯度场,求解势函数是困难的
4 旋度以及理解
在物理学中,常用向量场的旋度判断向量场是否为保守场
定义旋度的符号为$curl$,则旋度的计算方法定义如下: $$curl(\vec{F})=N_x-M_y$$ 容易发现,当$N_x=M_y$时,向量场$\vec{F}$的旋度为0,说明$\vec{F}$是保守场
- $M_y=N_x$在单连通区域成立的前提下,可推得$\vec{F}$是梯度场
- 梯度场是保守场,所以保守场都是无旋的(旋度为0)
在速度场中,旋度可以衡量运动在各个点上的扭转程度大小,旋度的值等于运动在旋转分量上的角速度的两倍,而旋度的正/负则分别对应顺/逆时针旋转
在力场中,旋度可以衡量物体上任一点受到的扭矩(力用于转动的分量),类似于加速度=力/质量的关系,角加速度=扭矩/转动惯量
5 参考:
