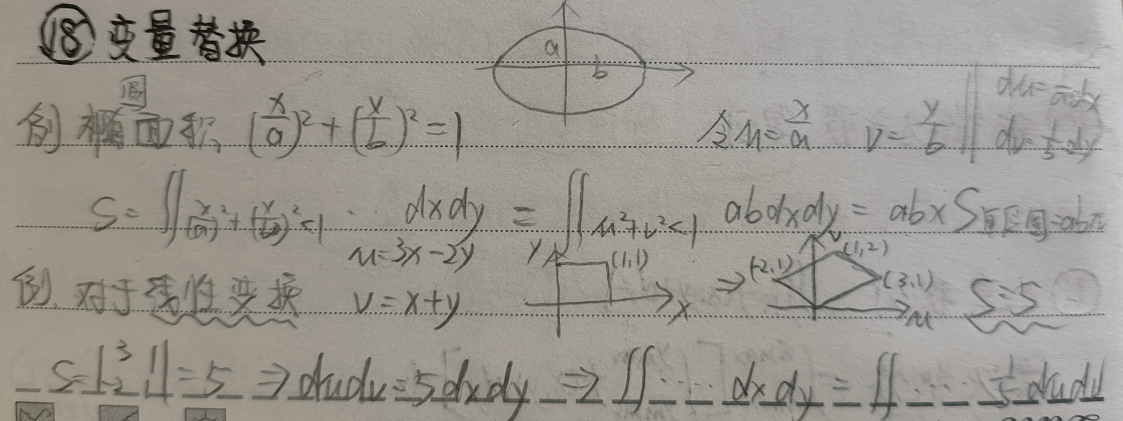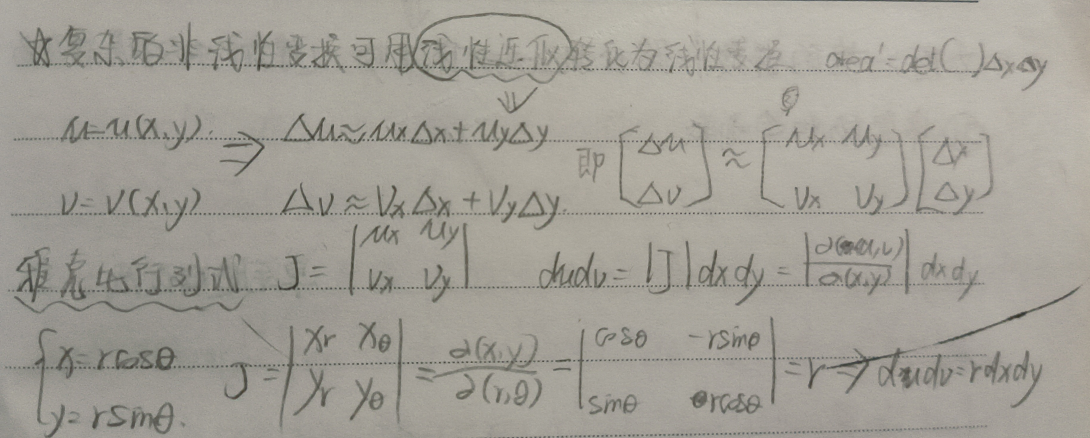1 变量替换的示例
在上一节中,从直角坐标系到极坐标的转换其实是一种换元法的特例: $$\int\int_Rf(x,y)dA=\int\int_Rg(r,\theta)rdrd\theta$$
在本小节,对这类方法进行拓展,并以例题的形式对变量替换法(换元法)进行说明
例题:计算$(\frac{x}{a})^2+(\frac{y}{b})^2=1$椭圆面积
分析:考虑借助$u=\frac{x}{a},v=\frac{y}{b}$进行换元
- 此时可得微分关系:$du=\frac{1}{a}dx,dv\frac{1}{b}dy$
- 借助积分计算椭圆面积$S$:
$$S=\int\int_{(\frac{x}{a})^2+(\frac{y}{b})^2<1}\cdot dxdy=ab\int\int_{u^2+v^2<1}dudv=ab\cdot S_{单位圆}=ab\pi$$
2 变量替换的思考
深入思考线性变换$u=3x-2y,v=x+y$的过程
考虑正方形$ABCD$(方便作为小格子贴近微分的几何解释)的线性变换过程
原始坐标为$A=(0,0),B=(0,1),C=(1,0),D=(1,1,)$的正方形
转换后为一个不规则四边形:$A'=(0,0),B'=(-2,1),C'=(3,1),D'=(1,2)$
借助行列式计算四边形的面积: $$S=\left| \begin{matrix} 3& 1 \\ -2 & 1 \\ \end{matrix} \right|=5$$ 所以$xy$坐标系中的每个小格子转换到$uv$坐标系中都会面积放大五倍,由此可知: $$dudv=5dxdy$$
以上结论仅适用于线性变换,但对于非线性变换可以通过线性近似转为线性变换
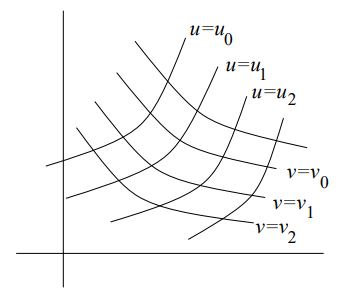
3 变量替换的一般过程
确定变量替换$u=u(x,y),v=v(x,y)$,并通过带入将$f(x,y)$替换为$g(u,v)$
对变量转换过程进行线性近似,并计算雅可比行列式:
线性近似:
$$\begin{equation} \left\{ \begin{gathered} \Delta u\approx u_x \Delta x+u_y \Delta_y \ \\ \Delta v\approx v_x \Delta x+v_y \Delta_y \end{gathered} \right. \end{equation}$$ 线性近似矩阵形式:
$$\left[ \begin{matrix} \Delta u \\ \Delta v \\ \end{matrix} \right] \approx \left[ \begin{matrix} u_x & u_y \\ v_x & v_y \\ \end{matrix} \right]\left[ \begin{matrix} \Delta x \\ \Delta y \\ \end{matrix} \right]$$ 由此可得:$dudv=Jdxdy=|\frac{\partial{(u,v)}}{\partial{(x,y)}}|dxdy$
其中$J$表示雅可比行列式(Jacobian): $$J=\left| \begin{matrix} u_x & u_y \\ v_x & v_y \\ \end{matrix} \right|$$ 3. 对积分上下限进行调整,得到变量替换后的积分形式 $$\int\int_{R(x,y)}f(x,y)dA=\int\int_{R(u,v)}g(u,v)Jdudv$$
补充说明:
- 线性近似能成立是因为当进行微分时,$\Delta x$趋近于无穷小,所以可忽略高阶项
- 此小节介绍的雅可比行列式只是二维形式,在其他场景可以是更高维的
4 参考