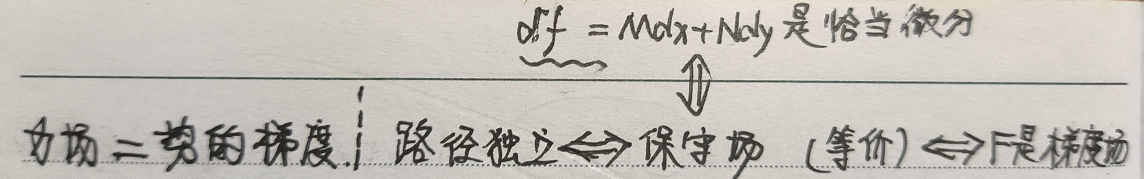1 梯度场与势函数
回归向量场的定义:$\vec{F}=M\vec{i}+N\vec{j}=<M(x,y),N(x,y)>$
假设存在一个函数$f(x,y)$,并且关系$f_x=M,f_y=N$成立,即: $$\vec{F}=<M,N>=<f_x,f_y>=\nabla f$$
则此向量场描述的是一个函数$f(x,y)$的梯度,$\vec{F}$也叫做梯度场,函数$f$叫做势函数
此处可关联物理学方便理解,$\vec{F}$描述的是重力场,则$f$描述的是重力势能。做功的计算既可以是力与位移的乘积,也可以说是对重力势能的变动描述:功=势能差
2 线积分基本定理
线积分是沿一条曲线对一个函数的梯度(向量场)做积分
假设曲线表示为$c$,曲线起点为$P_0$,曲线终点为$P_1$,则线积分基本定理如下: $$\int_c \nabla f\cdot d\vec{r} =f(P_1)-f(P_0)$$ 简略的证明过程: $$\int_c \nabla f\cdot d\vec{r}=\int_cf_xdx+f_ydy=\int_cdf =f(P_1)-f(P_0)$$ 简单举例:$\vec{F}=<y,x>$的势函数是$f(x,y)=xy$
注意,向量场有可能是梯度场,比如重力场和电场;也有可能不是,比如磁场
3 梯度场的性质
性质1:梯度场的线积分是路径独立的(做功只取决于始末点)
性质2:梯度场是保守场(对于闭合曲线$c$,$\int_c \vec{F}d\vec{r}=0$)
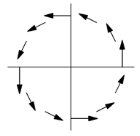
例题:判断向量场$\vec{F}=<-y,x>$是否为梯度场
分析,可通过计算向量场在闭合曲线(单位圆轨迹$c$)上的线积分结果进行判定(线积分结果为0表明向量场满足保守场的性质)
- 设$\hat{T}$表示沿轨迹切线方向(轨迹移动方向)的单位向量
- 根据轨迹和向量场可知,$\vec{F}$和$\hat{T}$是处处平行的
- 由于轨迹在单位圆上,所以$|\vec{F}|=1$
- 汇总以上信息,可知$\vec{F}\cdot \hat{T}=1$,所以线积分结果如下:
$$\int_c \vec{F}\cdot d\vec{r}=\int_c\vec{F}\cdot \hat{T}ds=\int_c1ds=2\pi\neq 0$$ 5. 所以向量场$\vec{F}=<-y,x>$不是梯度场
注:下一节将会有更便捷的证明方法
以下四种结论是等价的(可以互相转换的):
- 向量场$\vec{F}$是梯度场
- 向量场$\vec{F}$是保守场
- 向量场$\vec{F}$的线积分是路径独立的
- 向量场$\vec{F}$满足以下恰当微分形式:$f(x,y)=Mdx+Ndy$
4 参考