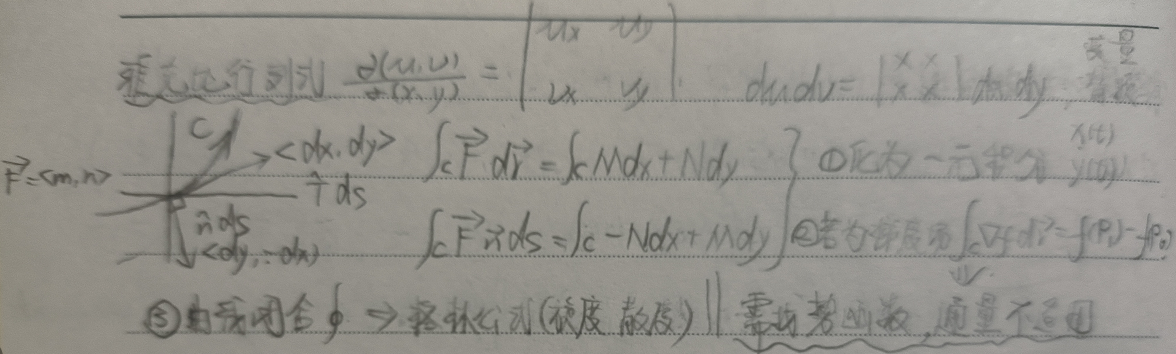1 单连通区域
单连通区域$R$:由单一的一块组成的区域$R$,即没有“洞”的区域
要求:对于单连通区域$R$内存在的任意闭合曲线$C$,曲线$C$的区域也属于$R$
不满足以上要求的区域则被称为多连通区域,或复连通区域
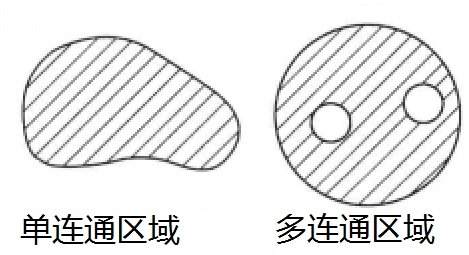
在之前第21节课中曾提及判定梯度场的前提条件,即$\vec{F}$处处有定义可导。在了解单连通区域的定义后,可以发现此前提条件等价于$\vec{F}$的定义域是单连通区域:
如果$\vec{F}$的旋度是0,且$\vec{F}$的定义域是单连通区域,则$\vec{F}$是保守场/梯度场
2 格林公式的拓展
原始的格林公式同样要求向量场$\vec{F}$在定义域内是处处由定义可导的,所以对于非连通区域,可以通过切分或贯通的方式将区域转换为单连通区域,再分别应用格林公式
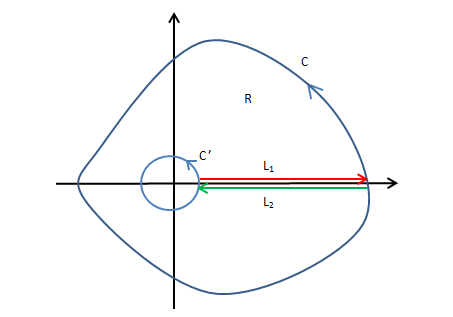
例如,针对闭合曲线$C$和$C'$围成的区域$R$,可以考虑构建可互相抵消的路径$L_1$和$L_2$使得非连通区域$R$转化为由${C,L_2,C',L_1}$围成的单连通区域,进而实现格林公式的拓展: $$\int \! \! \!\int_Rcurl(\vec{F})dA=∮_C\vec{F}\cdot d\vec{r}-∮_{C'}\vec{F}\cdot d\vec{r}$$
3 Unit 3 知识点简单概括
截止到第二十四节课,本课程的第三单元:平面上的二重积分和线积分(Unit 3 Double integrals and line integrals in the plane)部分内容已完成,内容脉络简单梳理如下:
- 二重积分的定义和计算(积分的集合含义、交换积分顺序)
- 二重积分与变量替换(极坐标、换元法、重心、转动惯量)
- 线积分与做功(向量场、梯度场、势函数、路径独立)
- 格林公式与通量(旋度、散度、通量、单连通区域)
补充说明1:二重积分的一般计算过程
补充说明2:线积分的常用计算方法
4 参考