1 异构图的定义与理解
异构图(Heterogeneous Graph),存在不同类型的节点和边
即节点和边至少有一个具有多种类型,常见于知识图谱的场景
举例:引文网络
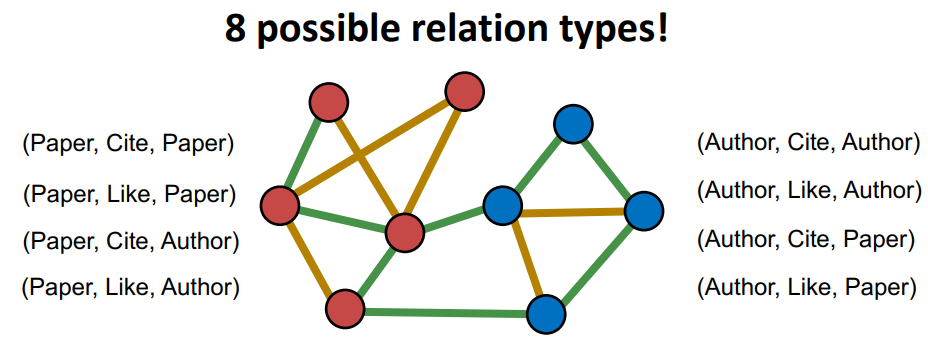
- 节点的类型可以是作者(Author)或文章(Paper)
- 边的类型可以是引用(Cite)或类似(Like)
从异构图到标准图:
- 可以将节点和边的类型视为
one-hot形式的特征,以此区分类型 - 比如将特征
[1, 0]附加到每个“作者节点”;将特征[0, 1]附加到每个“纸节点” - 但该方法不适用于不同类型节点维度不同、不同类型节点的边类型不同的情况
异构图的优点:一种更具表现力的图表示,能捕获实体之间不同类型的交互
异构图的缺点:计算和存储成本更高;图构建、训练和学习的难度更大
2 RGCN:异构图版 GCN
前置知识:2 经典 GNN 层之 GCN
核心技巧:对于不同的关系类型使用不同的神经网络权重 $W_r$
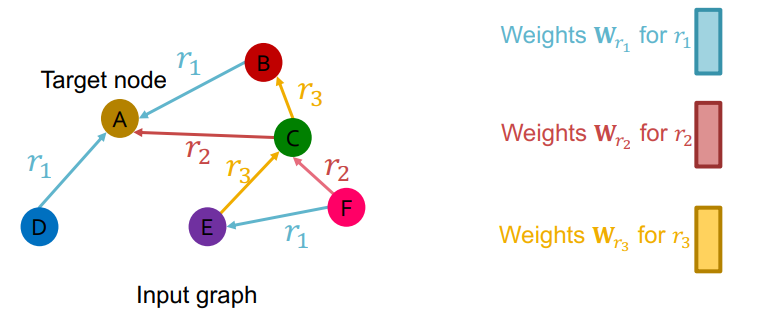
单层 RGCN 的计算过程如下: $$\mathbf{h}_v^{(l+1)}=\sigma\left (\sum_{r\in R}\sum_{u\in N_v^r}\frac1{|N_v^r|}\mathbf{W}_r^{(l)}\mathbf{h}_u^{(l)}+\mathbf{W}_0^{(l)}\mathbf{h}_v^{(l)}\right)$$
- 其中 $R$ 表示边类型的集合;$N_v^r$ 表示与边类型 $r$ 有关的节点集合
- $W_r$ 用于处理与边类型 $r$ 有关的邻节点信息;$W_0$ 用于更新节点本身的信息
RGCN 的问题:随着边类型的增长,参数量也会迅速增加(容易过拟合)
- 解决思路 1:分块对角矩阵(对权重矩阵进行稀疏化处理)
- 解决思路 2:部分参数共享,$V_b$ 是共享参数,而每个 $W_r$ 是 $V_b$ 的线性变换
预测任务:
- 节点预测任务和 GCN 一样,用最后一层进行分类预测概率输出
- 边预测任务需要额外的有监督训练,同时也需要虚构边作为负样本
细节补充:边预测任务的图切分
- 按照边类型进行图的"切分",并分别划分为四个集合
- 四个集合分别用于图结构学习、有监督学习、验证、测试
- 该方式避免样本稀少的边类型在验证集或测试集缺失数据
类似思路开源拓展到其他 GNN 模型,比如 RGraphSAGE、RGAT
3 HGT:异构图版 GAT
前置知识:4 经典 GNN 层之 GAT
问题:GAT 无法表示不同的节点和不同的边类型 原因:为每种关系类型引入一组神经网络对于注意力来说代价太高
HGT 的创新点:将注意力机制分解为节点注意力和边注意力
假如有 3 种类型的节点和 2 种类型的边;不分解的情况下,GAT 需要构建 $3\times 2\times 3=18$ 种注意力;而分解后,则只需要构建 $3+2=5$ 种注意力;注意力的构建成本得到了大幅降低
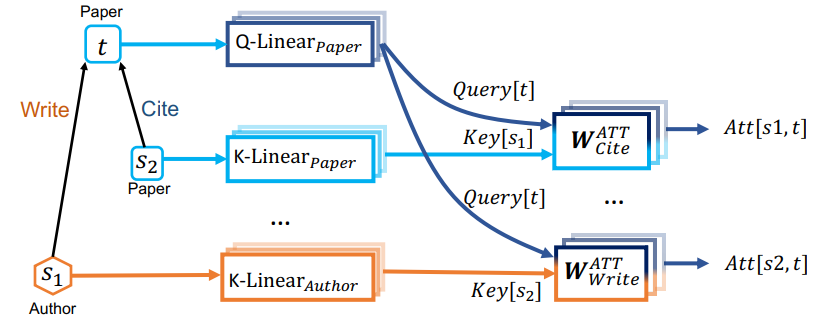
- 对于三元组
<s_2, Site t>,其对应的注意力得分来自 $W_{Cite}^{ATT}$ 矩阵 - 对于三元组
<s_1, Write t>,其对应的注意力得分来自 $W_{Write}^{ATT}$ 矩阵 - 注意力机制中的 $Q,K,V$ 也会根据节点类型的不同进行对应的线性变换 $Liner$
- 通过构建对节点/边类型敏感的 $Liner$ 和 $W^{ATT}$,HGT 实现了对异构图的理解
更多细节可参阅论文笔记:HGT:面向异构图的 Transformer
HGT vs RGCN:

- HGT 所需要的参数量少,并且最终性能表现更出色
4 异构图总结
从 标准图的 GNN 通用框架作为切入点,进行异构图的总结
- 信息转换(Message):需要针对边类型的不同进行不同的信息转换
- 信息聚合(Aggregation):先聚合同类型的信息,再聚合类型间的信息
- 层连接(Layer connectivity):一般 MLP 层也需要是对节点类型敏感的
- 图增强(Graph augmentation):可以同类型内采样或统计,也可以整图进行
- 预测(prediction):需要额外的考虑节点类型和边类型(区别不大)