1 单层图神经网络
图神经网络(GNN)的通用框架:
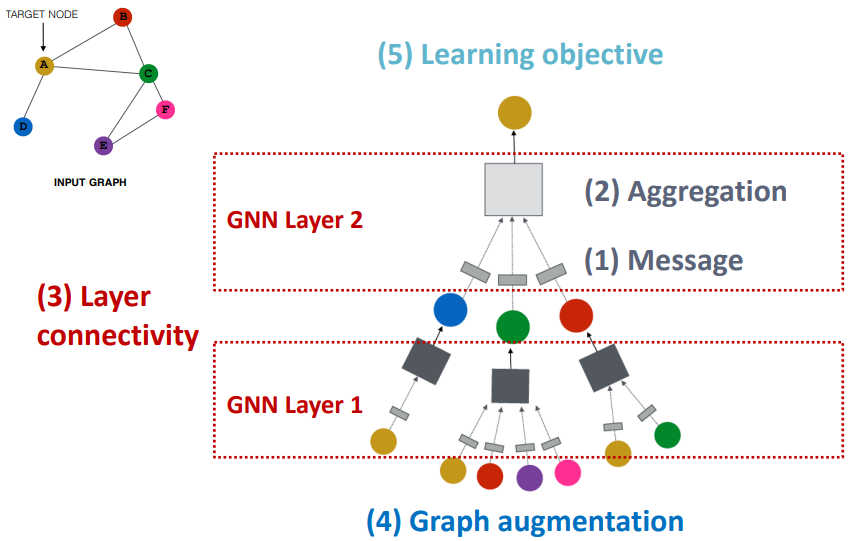
- 可以发现,GNN 层的输入为一组向量,输出为单个向量
- 所以单层 GNN 的核心过程在于邻域信息的转换(1)和聚合(2)
- 在转换和聚合邻域信息时,还要注意考虑节点本身的信息保留
所以单层 GNN 的计算过程可表示如下: $$ \begin{aligned} \mathbf{m}_u^{(l)}&=\mathrm{MSG}^{(l)}\left(\mathbf{h}_u^{(l-1)}\right),u\in{N(v)\cup v}
\\\mathbf{h}_v^{(l)}&=\mathrm{AGG}^{(l)}\left( \left\{\mathbf{m}_u^{(l)},u\in N(v)\right},\mathbf{m}_v^{(l)}\right)\end{aligned} $$
- 其中 $MSG$ 函数表示信息的处理和加工;$AGG$ 函数表示信息的聚合
- $\mathbf{h}_v^{(l-1)}$ 表示上一层的 $v$ 节点信息;$N(v)$ 表示 $v$ 节点的邻节点集合
- GNN 层将节点及其邻域信息加工为 $\mathbf{m}^{(l)}$,再聚合得到最终的输出 $\mathbf{h}_v^{(l)}$
常见的 AGG 函数包括 sum、mean、max
RNN 层一般会包含 ReLU、Sigmoid 等非线性激活函数来增强模型的表达力
2 经典 GNN 层之 GCN
GCN 是一种单层 RNN 的简单表示形式: $$ \begin{aligned} \mathbf{m}_u^{(l)}&=W^{(l)}\left(\frac{\mathbf{h}_u^{(l-1)}}{|N(v)|}\right)
\\\mathbf{h}_v^{(l)}&=\sigma(sum\left( \left\{\mathbf{m}_u^{(l)},u\in {N(v)\cup v\right}\right)\end{aligned} $$
- MSG 函数使用线性映射;AGG 函数使用 sum 聚合+sigmoid 激活函数
- 在 MSG 函数中,节点信息 $\mathbf{h}_u^{(l-1)}$ 会按照邻节点的数量进行标准化处理
在 GCN 的原始论文中,则使用了略有不同的标准化处理函数: $$ \mathbf{m}_u^{(l)}=W^{(l)}\left(\frac{\mathbf{h}_u^{(l-1)}}{\sqrt{|N(u)||N(v)|}}\right) $$
- 此处的标准化处理函数改动,减少了高度数邻居的权重
在 GCN 的原始论文中,借助切比雪夫实现了对卷积核的高效近似,进而推理出了 GCN 的高效等价方法。其对应的单层 GCN 的公式如下(矩阵形式): $$ H^{(l+1)}=\sigma(\widetilde{D}^{-1/2}\widetilde{A}\widetilde{D}^{-1/2}H^{(l)}W^{(l)}) $$
关于 GCN 的更多细节可参阅原论文:GCN_基于图卷积网络的半监督学习
3 经典 GNN 层之 GraphSAGE
GraphSAGE 在 GCN 的基础上,主要针对聚合方式进行了改进
GraphSAGE 会先聚合邻域信息,再进一步融合节点本身的信息: $$ \mathbf{h}_v^{(l)}=\sigma\left(\mathbf{W}^{(l)}\cdot\mathrm{concat}\left(\mathbf{h}_v^{(l-1)},\mathrm{AGG}\left( \left\{\mathbf{h}_u^{(l-1)},\forall u\in N(v)\right}\right)\right)\right) $$
- 上式中,AGG 函数包含了邻域信息的转换和初步聚合
AGG 函数可以采用任何可微函数,只要将多个向量聚合映射为单个向量:
- 取平均值(Mean):计算邻域信息的加权均值
$$ AGG=\Sigma_{u\in N(v)}\frac{\mathbf{h}_u^{(l-1)}}{|N(v)|} $$ 2. 池化(Pool): 一般使用最大池化函数 Max 或平均池化函数 Mean $$ AGG=Mean({MLP(\mathbf{h}_v^{(l-1)}),\forall u\in N(v)}) $$ 3. LSTM:对邻节点打乱排序后,应用 LSTM 聚合信息 $$ AGG=LSTM([\mathbf{h}_v^{(l-1)},\forall u\in N(v)]) $$
方法 1 中的 $1/|N(v)|$ 和方法 2 中 $MLP$ 是对邻域信息的转换,可替换或优化
GraphSAGE 还会通过层归一化处理,确保不同节点的嵌入表示具有相同的尺度
4 经典 GNN 层之 GAT
GAT 在 GCN 的基础上,主要针对聚合方式进行了改进: $$ \mathbf{h}_v^{(l)}=\sigma(\sum_{u\in N(v)}\alpha_{vu}\mathbf{W}^{(l)}\mathbf{h}_u^{(l-1)}) $$
- GAT 使用注意力得分 $\alpha_{v_u}$ 替代了原始 GCN 中的 $1/|N(v)|$
- 注意力得分能根据邻节点信息自适应的给出不同节点的权重
注意力得分的计算过程: $$ \begin{aligned} e_{vu}&=a(\mathbf{W}^{(l)}\mathbf{h}_u^{(l-1)},\mathbf{W}^{(l)}\boldsymbol{h}_v^{(l-1)}) \\
\alpha_{vu}&=\frac{\exp(e_{vu})}{\sum_{k\in N(v)}\exp(e_{vk})}\end{aligned} $$
- $e_{vu}$ 描述了节点 $u$ 的信息对节点 $v$ 的重要程度
GAT 的优缺点分析:
- 可以拓展为多头注意力,从更丰富的维度考虑信息的聚合
- 计算效率高(可并行),存储效率高(稀疏矩阵)
- 允许(隐式)指定不同的邻节点的重要程度($\alpha$)
- 仅考虑了局部的邻节点,不考虑全局的图结构
5 GNN 实践技巧
深度学习的常见技巧均适用于 GNN:
- Batch Normalization:稳定神经网络训练
- Dropout:防止训练的过拟合
- Attention/Gating:对信息流进行重要性评估或控制
- 非线性激活函数:ReLU、Sigmoid、PReLU
- 其他:比如层堆叠方式或添加跳层的连接(skip connections)
GNN 的过度平滑问题:
- 过渡平滑问题:所有节点嵌入收敛到相同的值
- 原因:随着 GNN 层的增加,每个节点的感受野会增强;而在图尺寸有限的情况下,节点的感受野会导致节点感受野的重叠和信息的同质化,并最终导致节点的嵌入高度相似
- 解决:控制好 GNN 的层数,确保节点具备合理的感受野
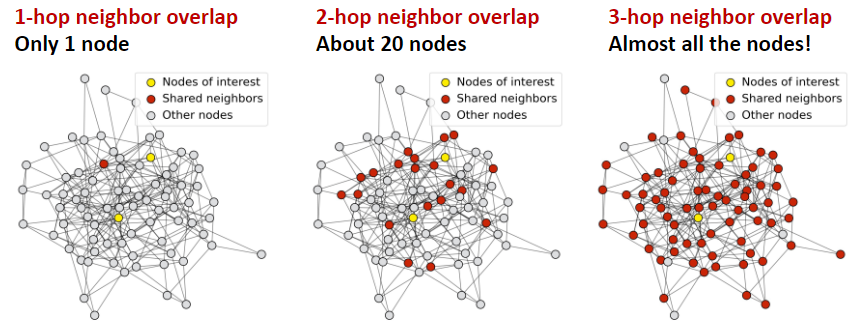
问题:如何在 GNN 层数有限的情况下,增加模型的表现力
- 方法 1:优化邻域信息的转换和聚合函数,比如使用深度神经网络
- 方法 2:添加其他类型的层(比如 MLP)来抑制邻域信息的传递
- 方法 3:合理利用跳层的连接(skip connections),增加早期层的影响
方法 3 更适用于 GNN 层数较多的情况,能缓解过度平滑问题
6 图的扩展与增强
原始的输入图可以通过图特征增强与图结构操作来丰富训练所需的计算图
图存在的问题与应对方法:
- 图特征缺乏:图特征增强
- 图过于稀疏:增加虚拟的节点/边
- 图过于密集:在信息传递时进行邻节点的采样
- 图规模过大:采样子图来进行嵌入表示的计算
方法 1 细节:图特征增强
- 对节点添加常量,计算方便易推广,但表现力一般
- 进行 one-hot 编码,维度高,表现力高,无法推广到新节点
- "循环计数"特征,能强化模型对结构周期性的表达能力
- 其他常见图特征:特征工程_图
方法 2 细节:增加虚拟的节点/边
- 可考虑在节点与 2 跳邻居节点间添加虚拟边
- 构建虚拟节点并关联到所有节点,改善稀疏图中的信息传递