中文标题:Mamba:选择性状态空间的线性时序建模
英文标题:Mamba: Linear-Time Sequence Modeling with Selective State Spaces
发布平台:预印本
发布日期:2023-12-01
引用量(非实时):201
DOI:
作者:Albert Gu, Tri Dao
关键字: #Mamba
文章类型:preprint
品读时间:2024-04-24 10:16
1 文章萃取
1.1 核心观点
本文以结构化状态空间模型(SSM)为基础提出了 Mamba 架构,Mamba 允许模型根据当前输入选择性地记忆或遗忘信息,而这种时间感知的引入阻碍了卷积结构 SSM 的并行化计算,为此 Mamba 设计了一种在循环结构下的并行扫描算法,并借助硬件感知实现计算加速。
实验分析发现,相比于 Transformer,Mamba 的推理速度快 5×,同时其计算性能随着时序长度呈线性增长;以 Mamba 作为主干的模型在不太下游任务中均有较好的性能表现
1.2 综合评价
- Mamba 在 S4 模型基础上进行了创新性调整,加入了自动信息选择机制
- Mamba 实现了循环结构的并行化,同时在内存和计算的成本上具备优势
- Mamba 在长序列等领域具备较大的优势,值得继续探索挖掘背后的潜力
1.3 主观评分:⭐⭐⭐⭐⭐
2 精读笔记
原始论文不推荐缺乏 SSM 相关前置知识的读者直接观看
建议优先阅读本笔记进行知识补齐,或者本人推荐的[第三方参考](A Visual Guide to Mamba and State Space Models]( https://newsletter.maartengrootendorst.com/p/a-visual-guide-to-mamba-and-state )
2.1 状态空间模型
状态空间模型(State Space Models,SSM)
- 源自传统的控制理论,即通过状态变量对动态系统进行建模
- SSM 根据当前状态表示 $h(t-1)$ 和输入信息 $x(t)$ 来预测未来的状态 $y(t)$
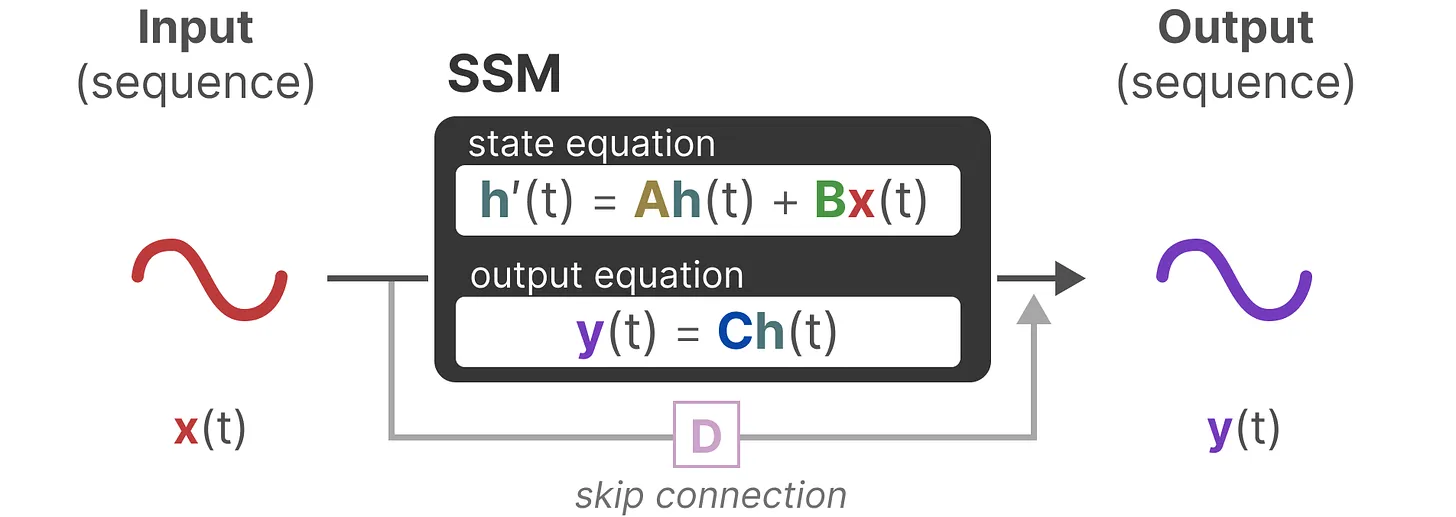
- 系数矩阵 $A,B,C,D$ 均是可学习参数,其中 $D$ 类似 skip-connection
- $A\in \mathbb{R}^{N\times N}$ 表示状态转移矩阵,$B\in \mathbb{R}^{N\times 1}$ 表示输入门,$C\in \mathbb{R}^{N\times 1}$ 表示输出门
- 矩阵 D 通常不包含在 SSM 模型内部,SSM 模型的整体计算细节如下:
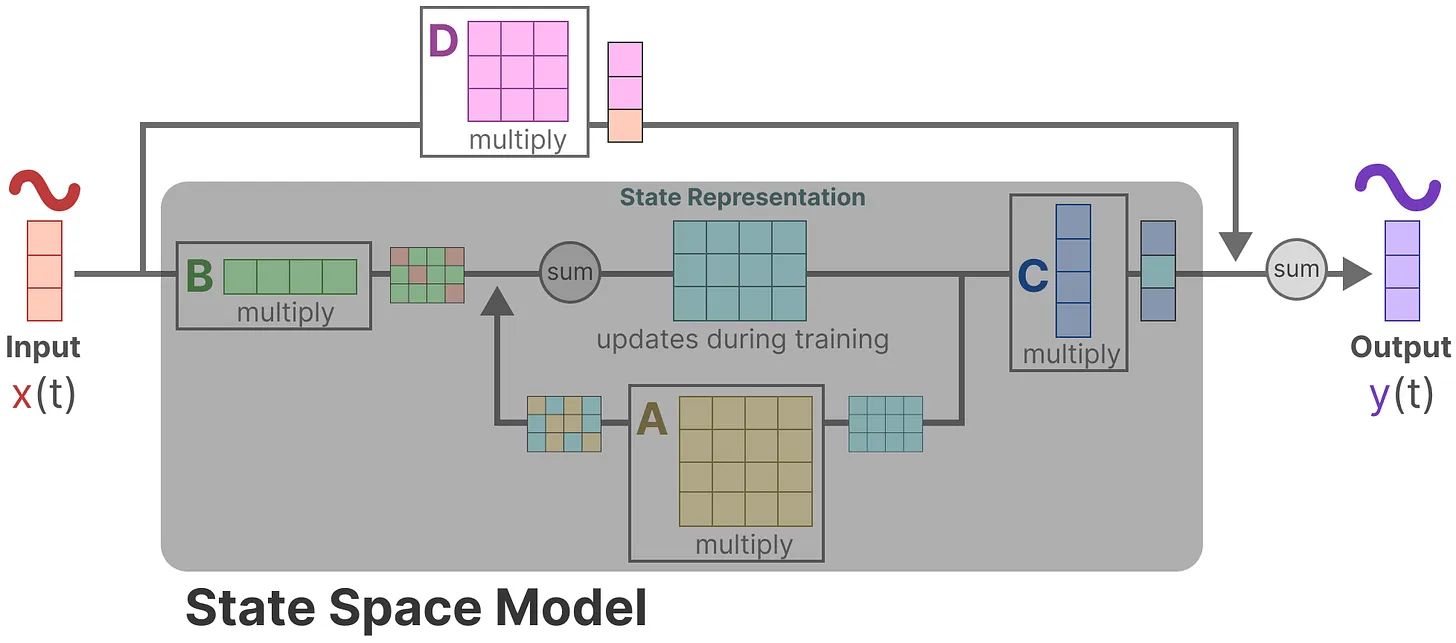
SSM 的结构与 RNN 很相似,只是把权重系数替换为了矩阵系数,去掉了非线性激活
其中状态转移矩阵 $A$ 对应 RNN 中的隐藏状态(hidden state),用于历史信息的总结
2.2 S4:结构化 SSM 时序建模
S4 架构:一种用于超长距离序列建模任务的 SSM
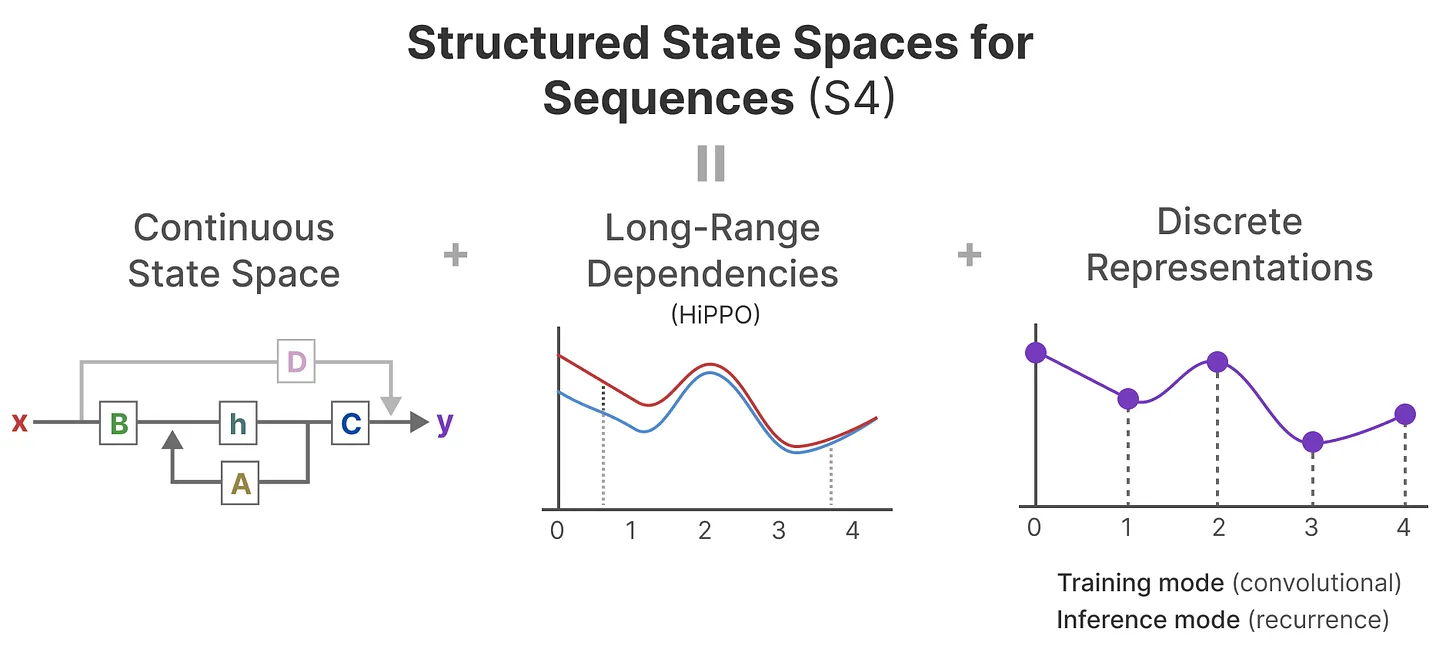
- S4 架构主要包含三个部分:连续信号的 SSM(上一节已介绍)、HiPPO 矩阵捕捉长期的信息依赖、离散信号下的结构化 SSM(卷积结构与循环结构)
2.2.1 S4 细节 1:处理离散信号
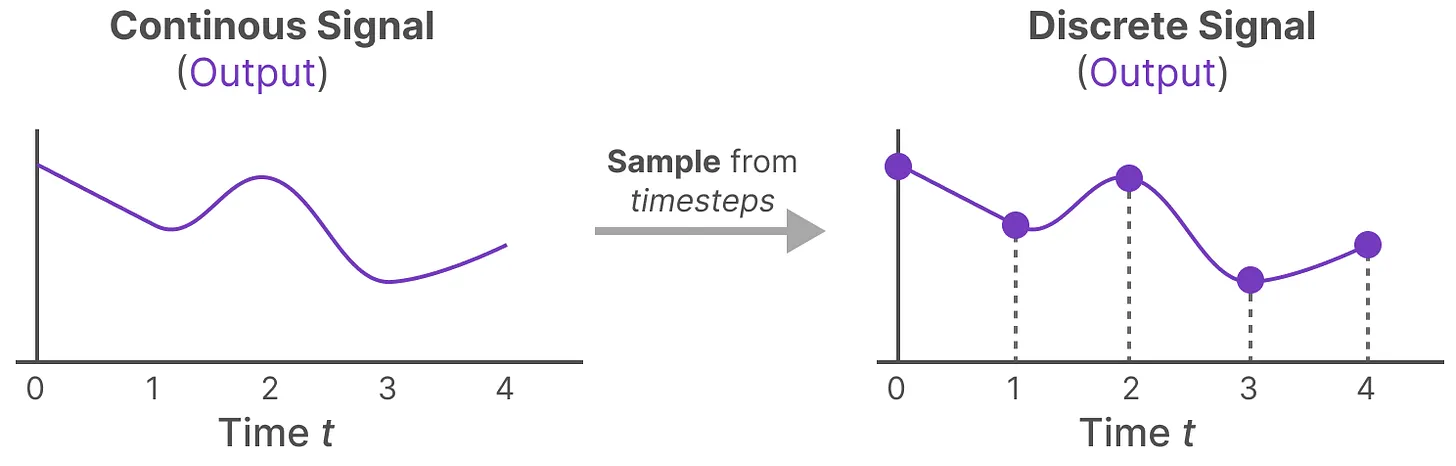
零阶保持技术 (Zero-order hold technique)——从连续信号到离散信号
- 文本序列一般为离散信号,因此需要引入额外的参数 $\Delta$ 来构建连续信号
- 参数 $\Delta$ 被称为步长(step size),实现对输入的阶段性保持(resolution)
- 每次接受到的离散信号后,都保持该值不变,只到接收到新的离散信号:
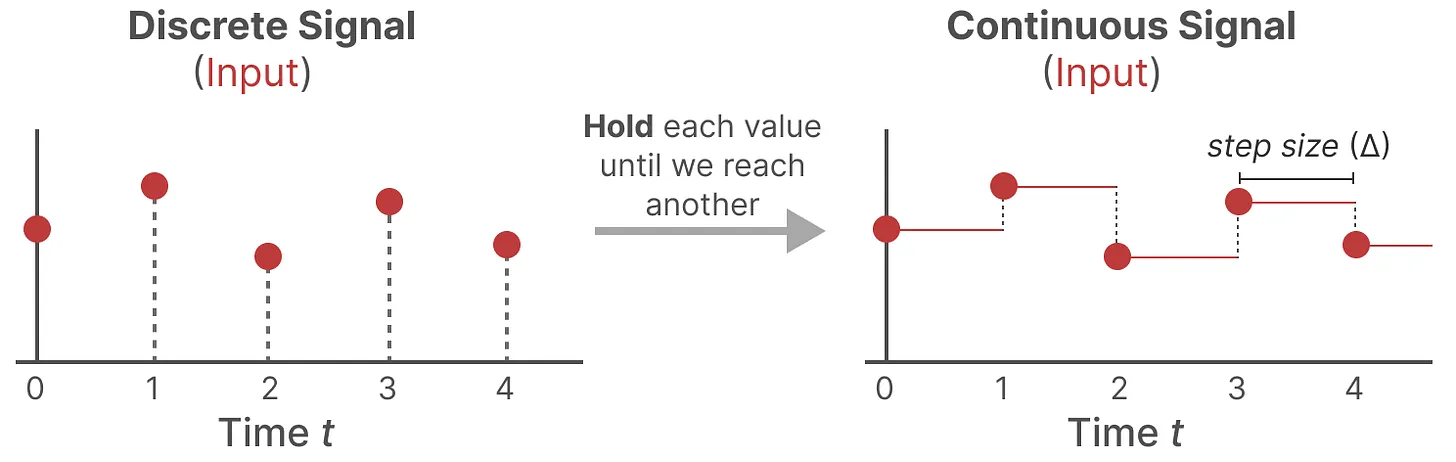
- 模型输出阶段,按照步长 $\Delta$ 对连续信号进行采样,得到离散信号
数学形式上,使用以下方式来应用零阶保持:
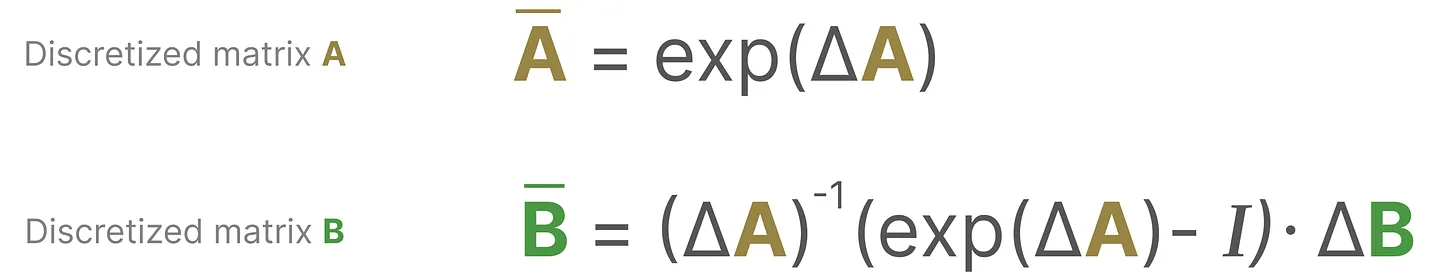
2.2.2 S4 细节 2:结构化 SSM
状态空间模型的结构化:主要考虑循环结构和(一维)卷积结构两种情况
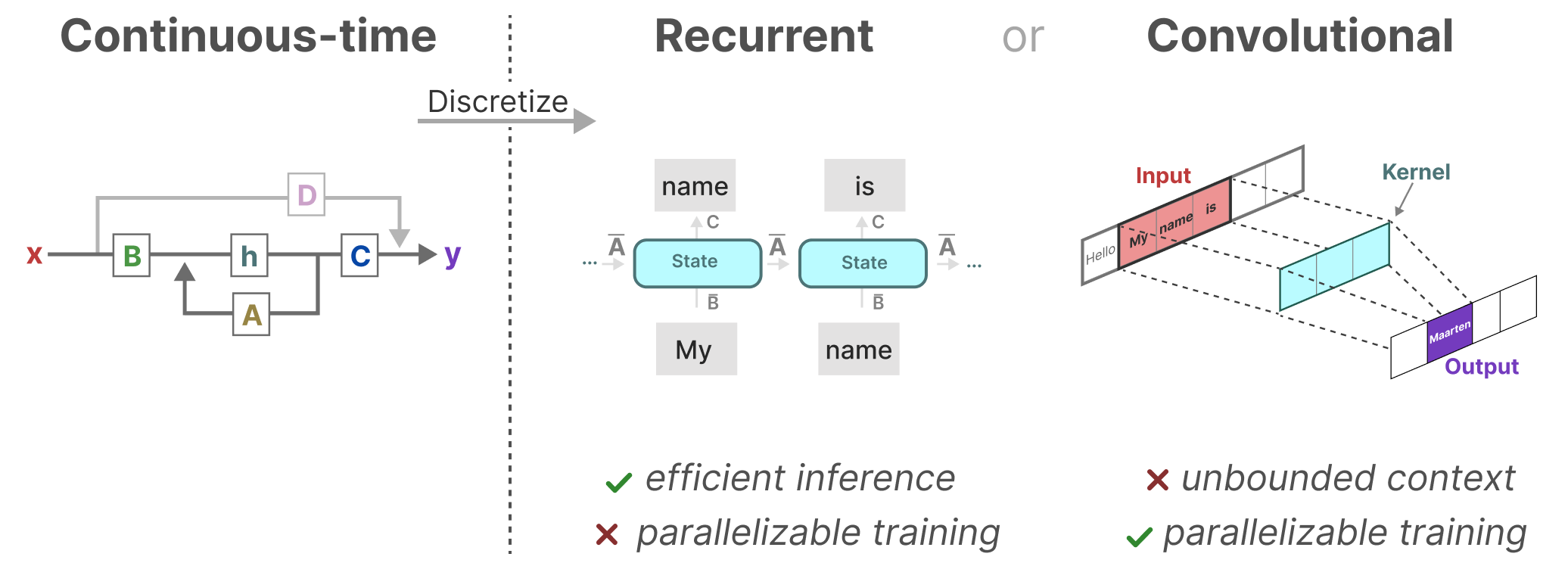
- 循环结构的优势是能实现推理高效且支持可变的序列长度,但不支持并行训练
- 卷积结构的优势是能实现更高效的训练(可并行训练),但对序列长度有要求
- 两种结构中,状态表示都具备线性时间不变性 (Linear Time Invariance,LTI)
- LTI 意味着 SSM 的矩阵参数($A,B,C$)对于所有时间步长是固定不变的;即对于任意的输入序列,SSM 使用相同的矩阵参数,SSM 在不感知时间的情况下实现输入的静态表示
思考:如何同时发挥循环结构的推理优势和卷积结构的训练优势?
S4 架构的亮点在于打通了 SSM 的循环结构和卷积结构
在循环结构的情况下,SSM 的计算过程如下(初始化 $x_{-1}=0$): $$ \begin{aligned} &\text{h}_{0}=\bar{B}x_{0} \\ &y_{0} =Ch_0=C\bar{B}x_0 \\ &\text{h} _1=\bar{A}h_0+\bar{B}x_1=\bar{A}\bar{B}x_0+\bar{B}x_1 \\ &y_{1} =Ch_{1}=C\left(\bar{A}\bar{B}x_{0}+\bar{B}x_{1}\right)=C\bar{A}\bar{B}x_{0}+C\bar{B}x_{1} \\ &\text{h} =\bar{A}h_{1}+\bar{B}x_{2}=\bar{A}\Big(\bar{A}\bar{B}x_{0}+\bar{B}x_{1}\Big)+\bar{B}x_{2}=\bar{A}^{2}\bar{B}x_{0}+\bar{A}\bar{B}x_{1}+\bar{B}x_{2} \\ &y_{2} =Ch_{2}=C\Big(\bar{A}^{2}\bar{B}x_{0}+\bar{A}\bar{B}x_{1}+\bar{B}x_{2}\Big)=C\bar{A}^{2}\bar{B}x_{0}+C\bar{A}\bar{B}x_{1}+C\bar{B}x_{2} \\ &y_{k} =C\bar{A}^{k}\bar{B}x_{0}+C\bar{A}^{k-1}\bar{B}x_{1}+\cdots+C\bar{A}\bar{B}x_{k-1}+C\bar{B}x_{k} \end{aligned} $$ 以上计算过程可以向量化为卷积运算,定义卷积核 $\overline{K}$: $$ \begin{aligned} \overline{K}&=(C\overline{B},C\overline{AB},\ldots,C\overline{A}^{k-1}\overline{B})\in\mathbb{R}^K \\ y_{k} &= x * \overline{K} \end{aligned} $$
- 其中 $L$ 表示模型的层数;$\overline{A,B}$ 表示零阶保持中的矩阵参数
- 由于离散矩阵参数满足 LTI,因此在实际训练中每次迭代前提前计算好 $\overline{K}$
至此 S4 便可以在训练时借助卷积实现并行化,在推理时转化为循环结构的 SMM
2.2.3 S4 细节 3:HiPPO 矩阵
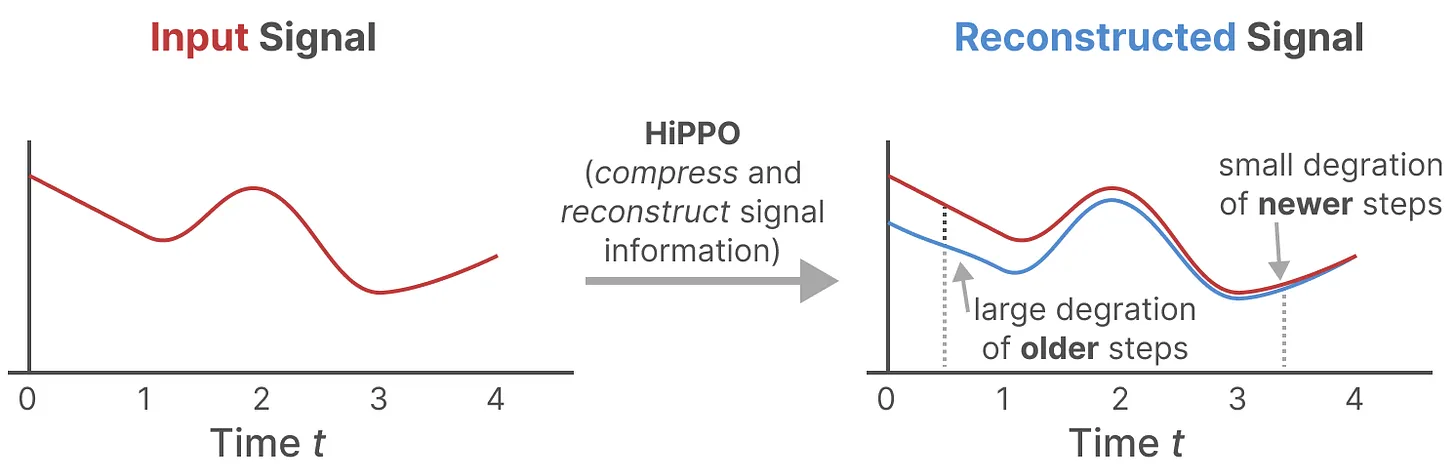
HiPPO 矩阵:
- 类似于 RNN,普通循环结构中的状态转移矩阵 $A$ 只能记录有限的状态信息
- HiPPO 矩阵会尝试将过去的所有输入信号压缩成一个系数向量,因此借助 HiPPO 矩阵来初始化 $A$ 可以更好地近似历史信息/重建近期信号,并实现模型对更长期信息的依赖
- HiPPO 矩阵初始化可以显著提升 SSM 在 MNIST 上的基准性能(60%->98%)
HiPPO 矩阵的定义如下:
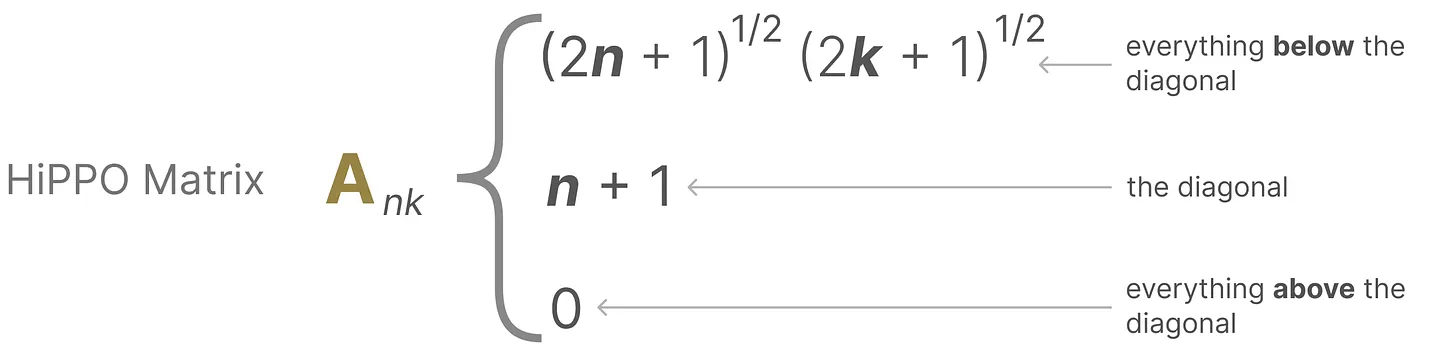
HiPPO 矩阵的示例:
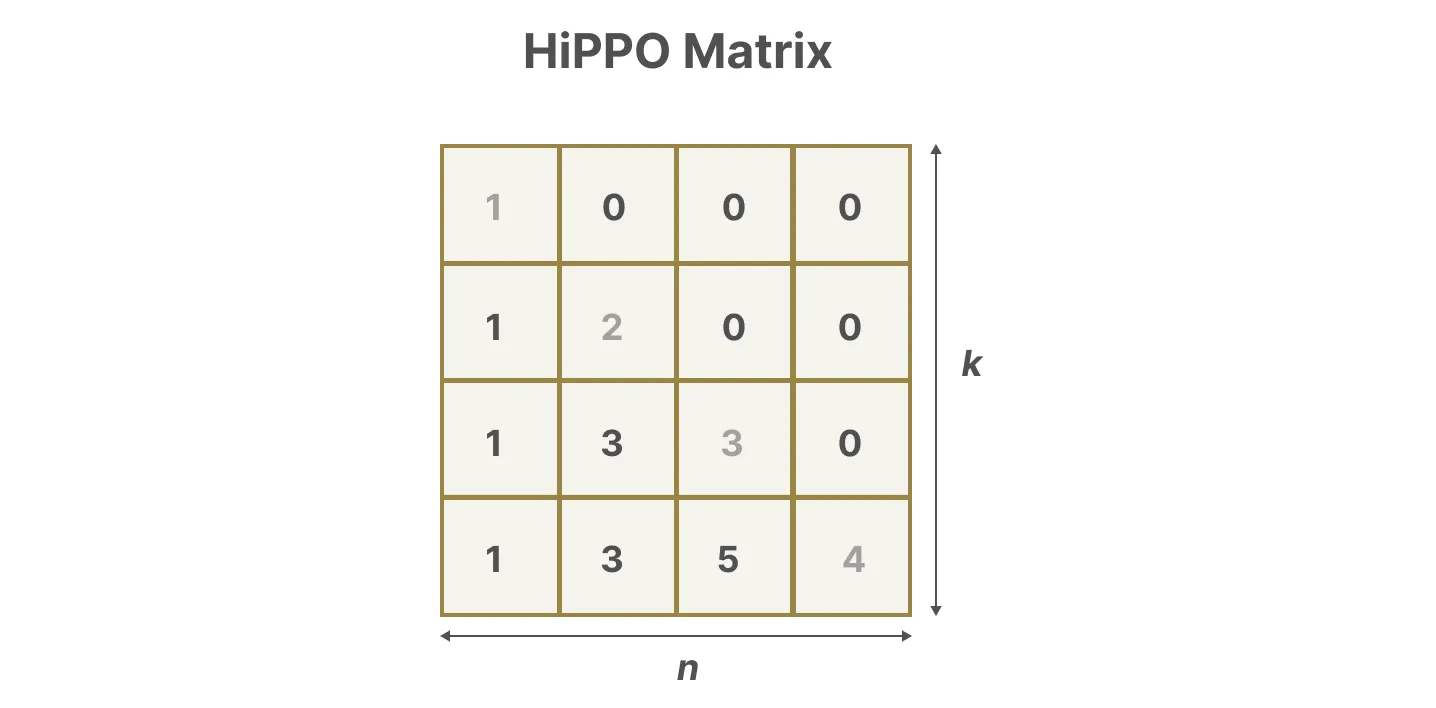
数学理解,HiPPO 矩阵通过跟踪勒让德多项式的系数来实现历史信息的近似
除了以上技术细节,S4 架构还在 HiPPO 矩阵部分进行了很多计算和内存使用上的优化,缓解长序列容易引起的梯度消失/爆炸问题。比如通过针对矩阵 $A$ 进行对角线加低秩(DPLR)处理;或者在快速傅里叶 FFT 在频率空间计算 SSM 的截断生成函数
关于 S4 架构或 HiPPO 的更多技术细节和代码实现可参阅 The Annotated S4
2.3 从 S4 到 Mamba
Mamba 是一种具备选择性的 SSM
- Mamba 允许模型过滤掉不相关的信息,并无限期地记住重要的信息
- Mamba 通过硬件感知算法克服了 SSM 中的 LTI 约束,实现性能加速
2.4 Mamba 细节 1:信息的选择
目前 S4 架构的局限性:
- Transformer 能根据输入序列动态计算注意力得分,从而进行信息的过滤
- 而在 SSM 中,矩阵 A、B 和 C 的静态性质限制了模型对内容的感知问题
S4 架构中的关键矩阵参数:
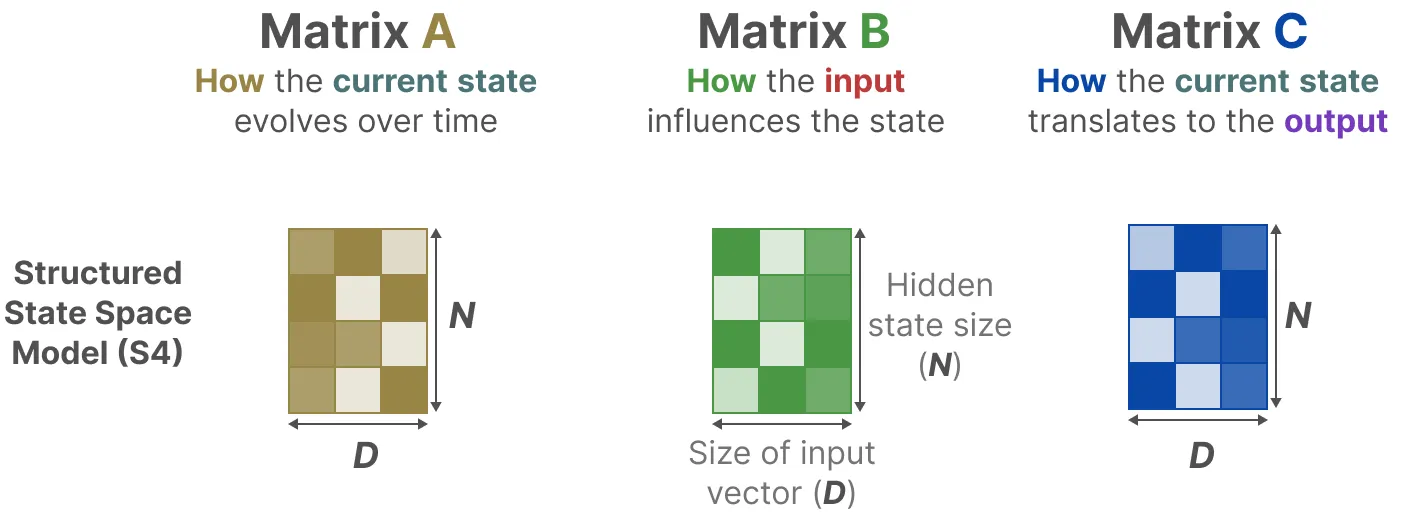
已知输入 $x_k \in \mathbb{R}^{B\times L\times D}$,输出 $y_k \in \mathbb{R}^{B\times L\times D}$
其中 $B$ 表示 batch size;$L$ 表示序列长度;$D$ 表示输入向量的维度
Mamba 架构中的关键矩阵参数:
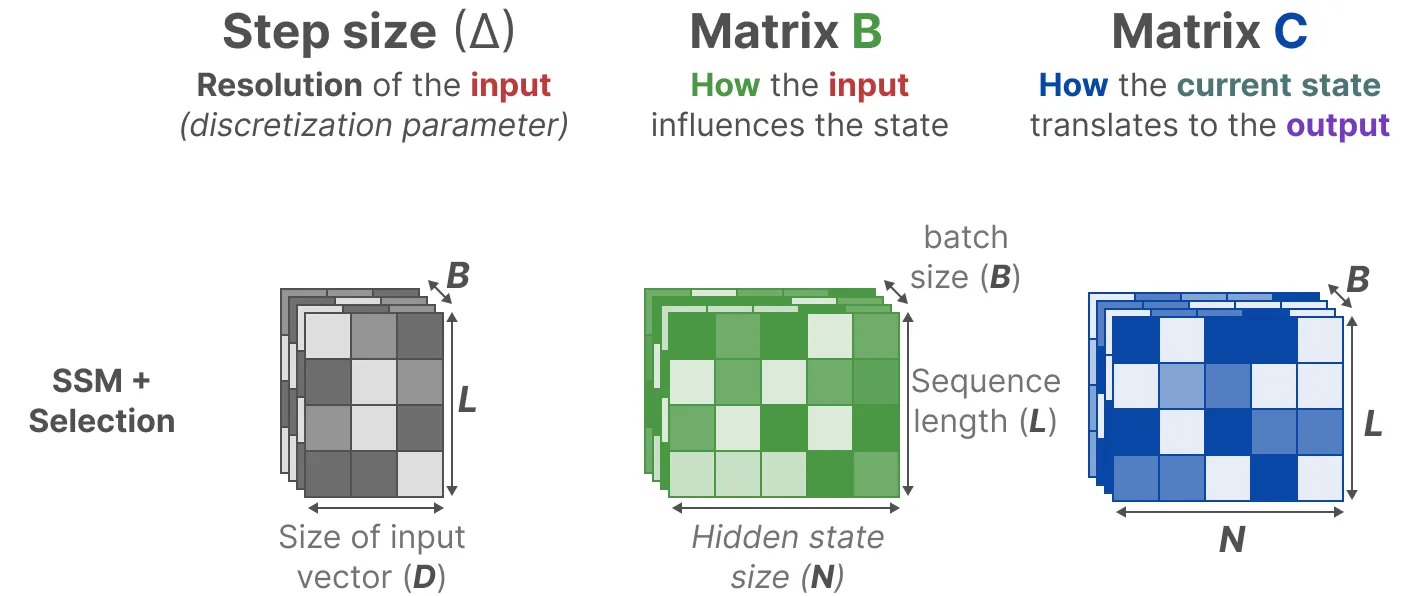
- Mamba 改变了关键矩阵参数的张量/维度设计,使得它们具备了时间感知性;即矩阵 $\Delta,B,C$ 会随着输入的序列长度 $L$ 或 batch size $B$ 的变动而改变
- 在 Mamba 中状态转移矩阵 $A$ 保持不变,但影响状态的方式($B,C$)是动态的
- 较小的步长 $\Delta$ 会使得模型更关注历史信息;反之则会使得模型更关注当前的输入
至此,Mamba 架构实现了对信息的选择(自主选择信息在隐藏状态中的保留与删除)
思考:Mamba 对 S4架构的改动,引入了具备时间感知性的动态矩阵参数,违反了 LTI 约束;SSM 模型循环结构无法转化为卷积结构,也就无法在训练阶段实现并行化计算
2.5 Mamba 细节 2:并行与硬件感知
复习:RBB 的扫描操作(scan operation)
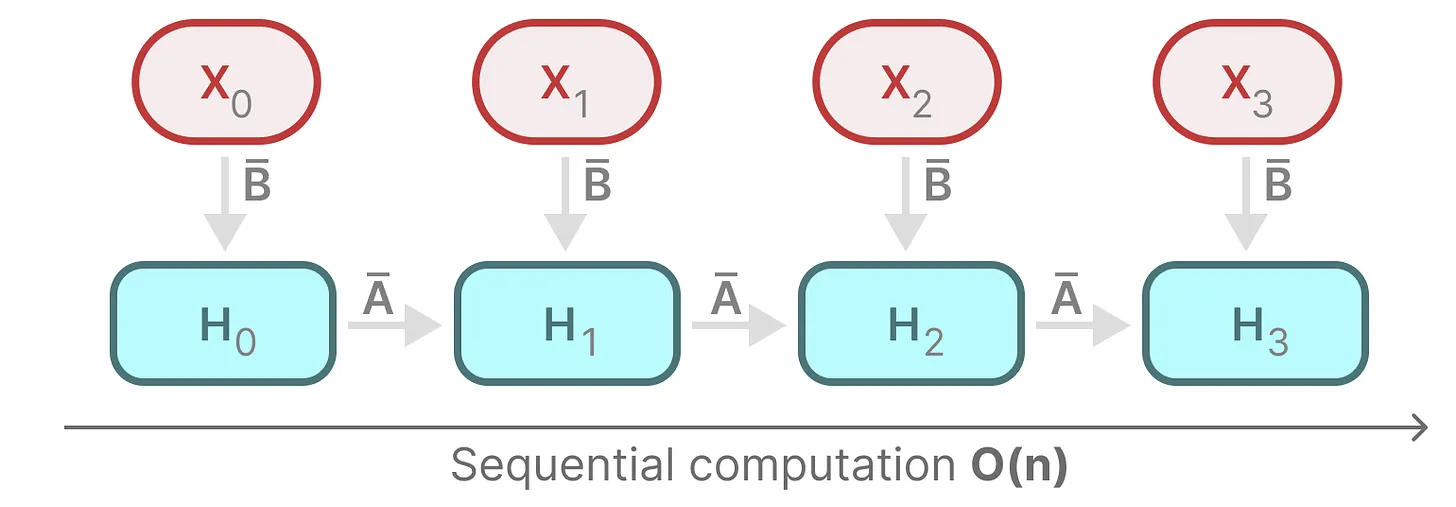
- 上图展示了扫描操作的基本过程,该计算循环过程很显然不适合并行化计算
Mamba 通过计算部分序列并迭代组合,来实现并行扫描算法:
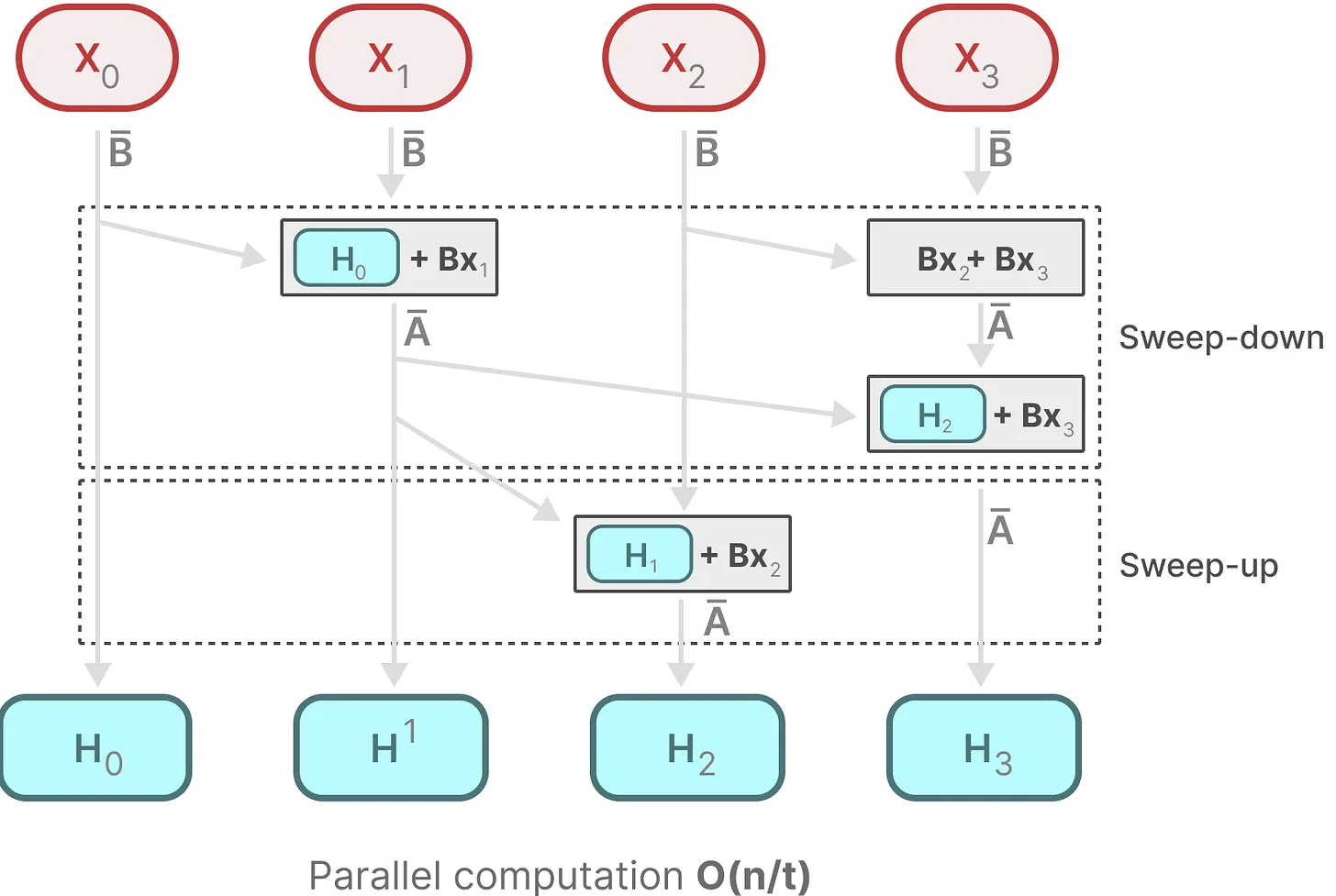
SRAM:常用于 GPU 中的 L1、L2 缓存,高功耗,低容量,低延迟
DRAM:常用于 GPU 中的显存,功耗更低,容量更大,但延迟更高
硬件感知算法 Hardware-aware Algorithm:
- GPU 的缺陷: SRAM 和 DRAM 之间的频繁通信导致的计算瓶颈
- 类似 Flash Attention,Mamba 通过核融合限制 SRAM 和 DRAM 间的通信次数
- 在 SRAM 中积累一批结果再集中写入 DRAM,从而降低来回读写的次数

最后,硬件感知算法不会保存中间状态,而是在后向传递时对中间状态进行重新计算;因为重新计算的成本,比从相对较慢的 DRAM 中读取中间状态的成本更低
2.5.1 Mamba 架构总结
最终的 Mamba 计算流程可表示如下:
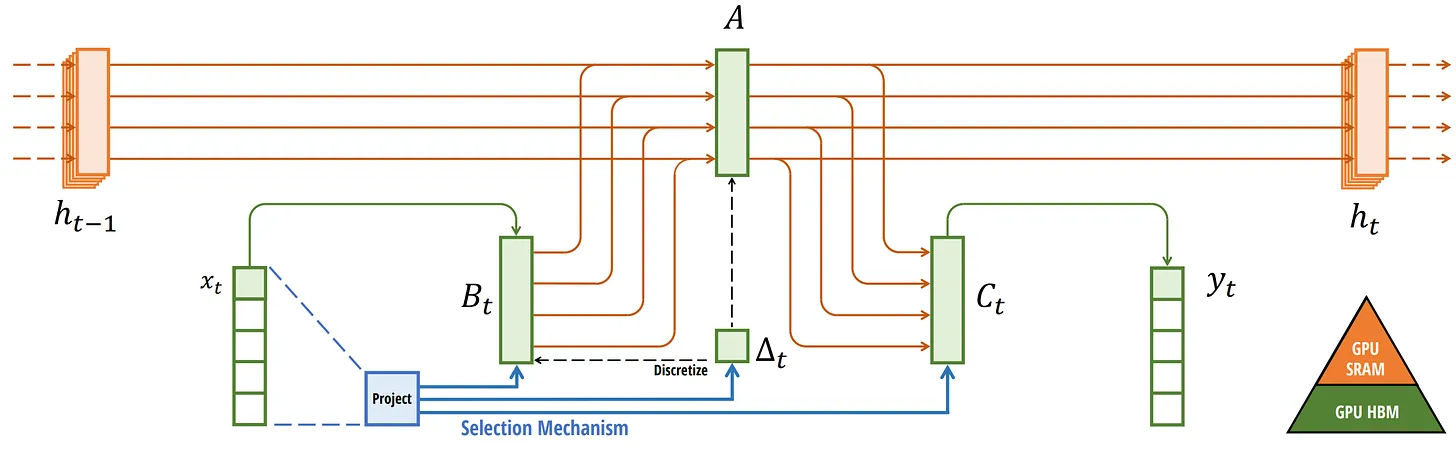
- 针对输入 $x_t$ 进行选择性扫描和压缩(Selection Mechanism,Project)
- 通过步长 $\Delta_t$ 和零阶保持对离散信号进行处理(Discretize)后进入结构化 SSM
- 结构化 SSM 模块先收集来自输入门 $B_t$ 的信息和历史潜在表示 $h_{t-1}$,然后经过状态转移矩阵 $A$ 更新潜在表示得到 $h_{t}$,并最终通过输出门 $C_t$ 实现对目标的预测 $y_t$
- 矩阵 A 通过 HiPPO 初始化捕获长程依赖关系;并行扫描和硬件感知算法用于计算加速
类似于 Transformer,Mamba 可融入任意的神经网络模型
Mamba 块:
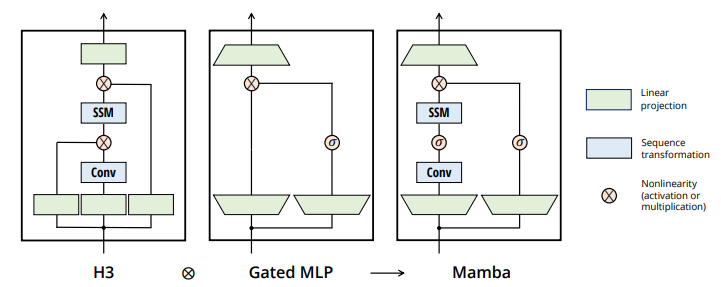
- H3(Hungry Hungry Hippo)是一种经典的 SSM 架构
- 本文通过组合 H3 与门控 MLP,提出了 Mamba 块的基本结构
重复 Mamba 块,与标准归一化和残差连接交错,形成 Mamba 模型架构:
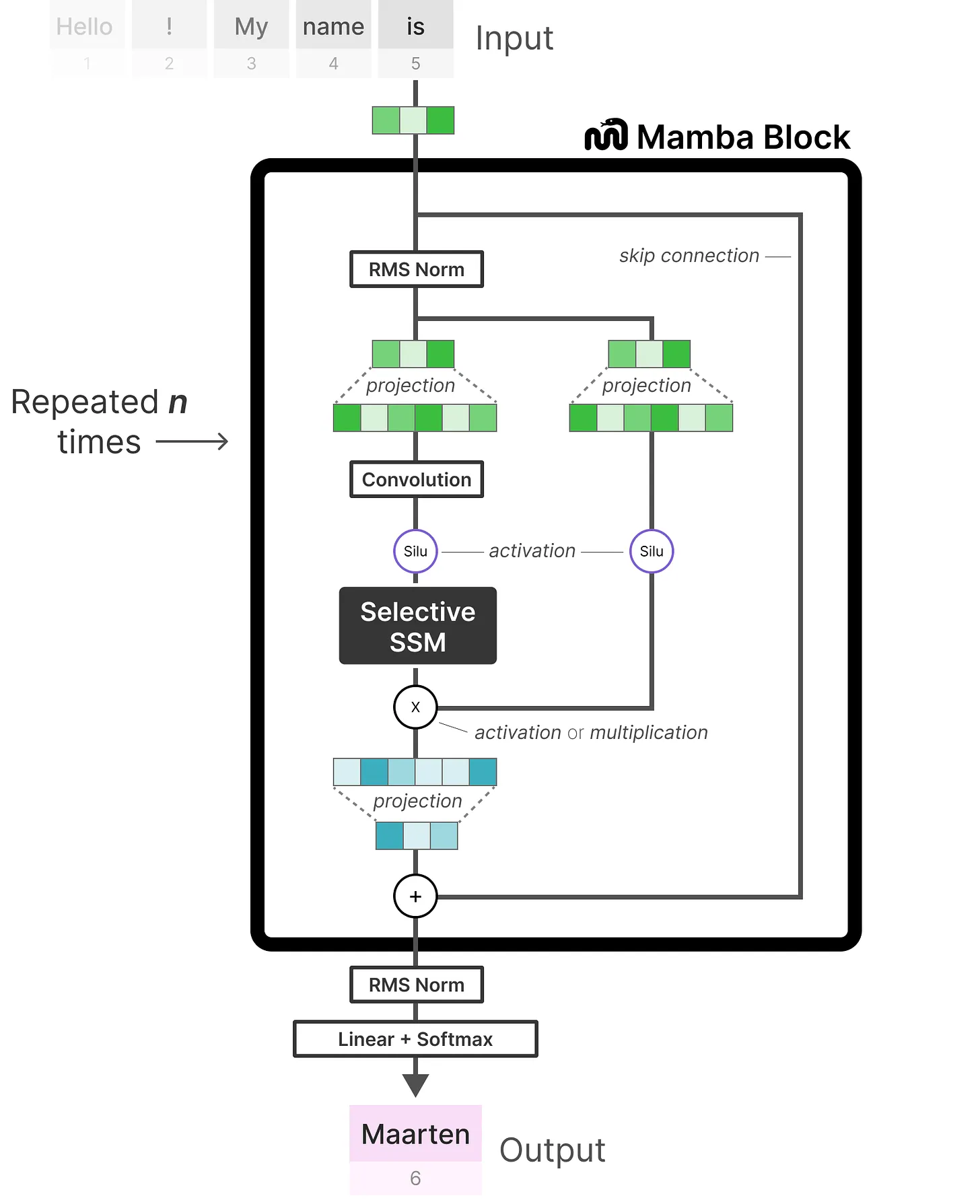
2.6 实验结果分析
用于对比模型盘点:
- Hyena:使用全局卷积来近似 SSM,在音频和视觉等领域表现出色
- RWKV:基于线性注意力近似,旨在为语言建模设计高效的 RNN
- RetNet:通过引入额外的门控来优化 SSM 的并行计算路径
- H3++:结合了线性注意力和 SSM,通过门控连接来增强模型的性能
- Transformer++:当前最优的 Transformer 架构,计算快效果好
在 Chinchilla 缩放定律下预训练时,语言任务优于同类开源模型:
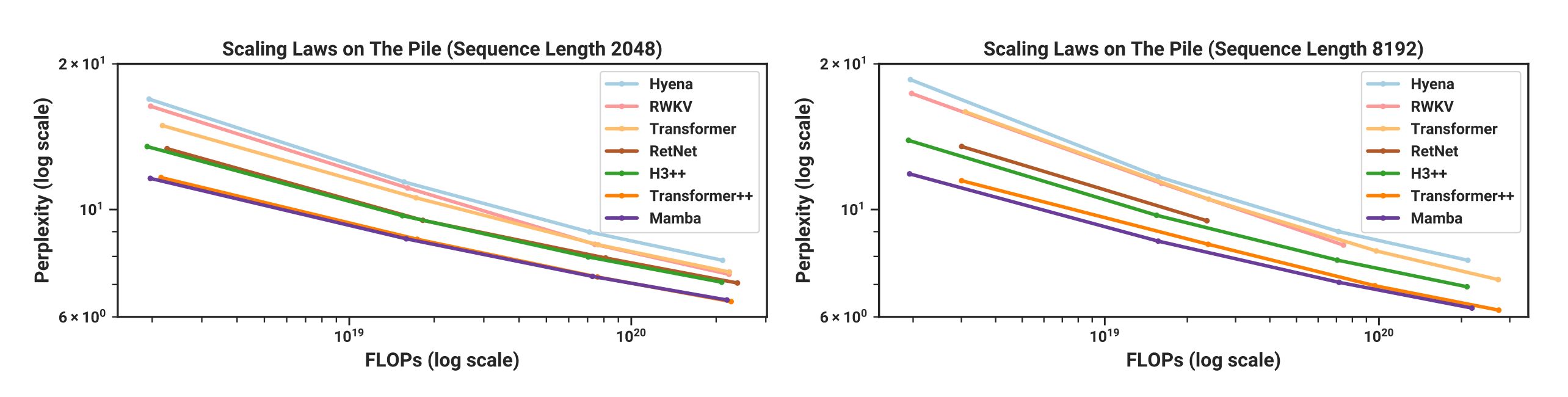
- 左图对应序列长度为 2048 的情况;左图对应序列长度为 8192 的情况
- 最终效果(评价指标为困惑度 perplexity,越低越好)打平 Transformer++
随着时序长度的增加,Mamba 计算耗时更少并且不会内存溢出:
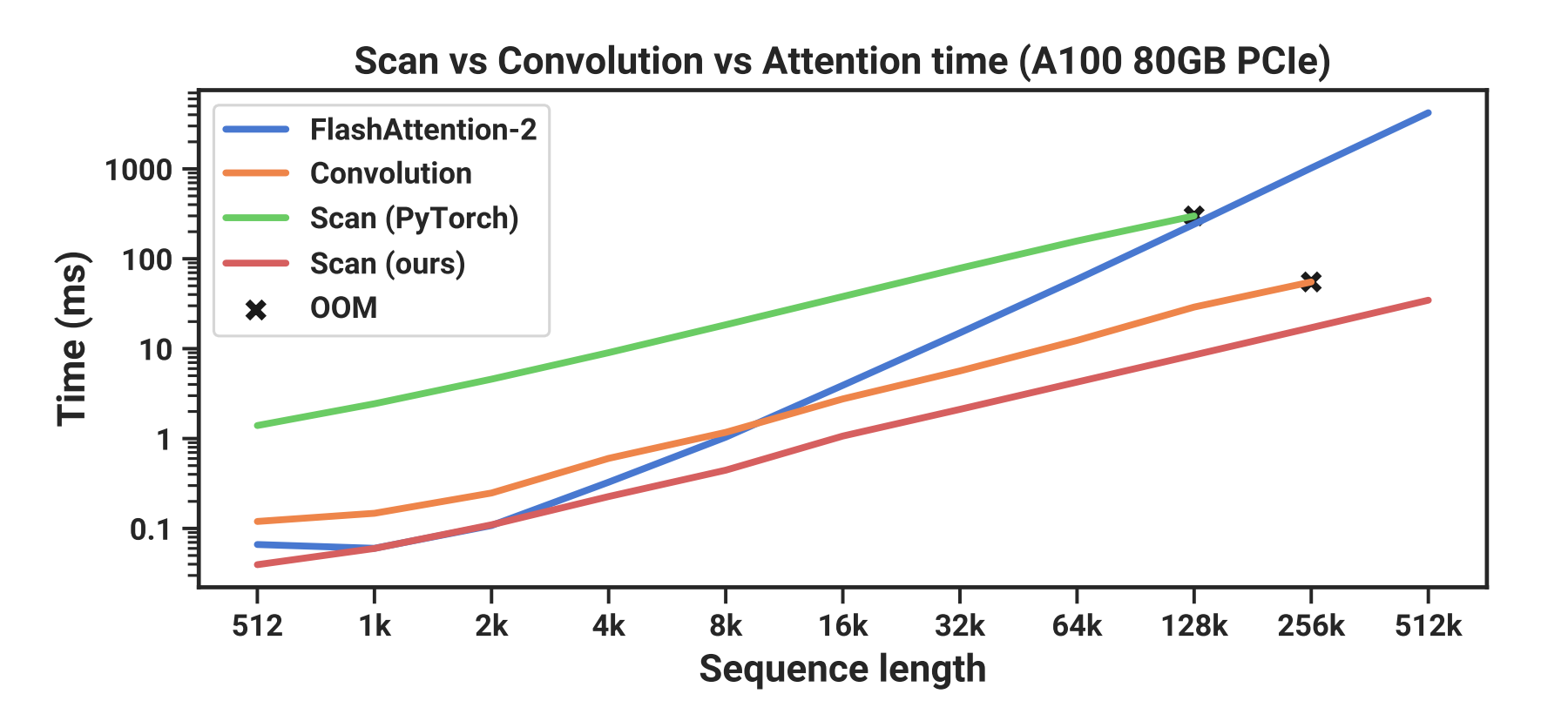
运行效率分析:
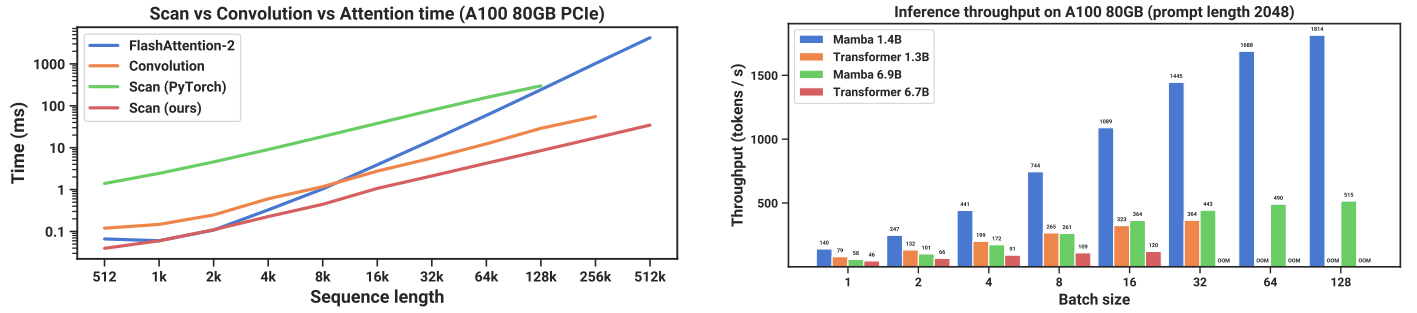
- 左子图结论:本文提出的并行扫描算法比 PyTorch 的标准实现快 40×
- 右子图结论:作为循环模型,Mamba 的计算吞吐量比 Transformer 高 5×
消融实验小结:
- Mamba 块与 H3 块的差异不大,性能差异主要体现在选择性 SSM
- $\Delta$ 是最重要的参数,对模型性能影响最大;$\Delta$ 即使是 1 维也是有效的
- 增加 SSM 中的隐藏状态维度 $N$ 能显著提高性能,同时总参数量增加不大
其他结论:
- Mamba 适用领域广泛,尤其适合基因组、音频和视频等长时序的情况
- 本文实验多局限于小规模数据,不确定 Mamba 在大尺度模型上的表现
论文作者在后续补充实验中验证了 Mamba 在 3B 参数量下依然表现出色
3 论文后续
Mamba 的名称起源:因为架构中有太多的 ssss 了(蛇的拟声)
RNN VS Mamba(摘自理解 Mamba 模型 - 董鑫)
| 改动 | 效果 |
|---|---|
| Mamba 去掉了 RNN 的非线性 (tanh) | 方便在序列上进行多线程计算, 更适合 GPU |
| Mamba 的 hidden state 的维度比较高 | Mamba 的隐藏状态是 $D\times N$;一个更大的 hidden state 更利于记住更多东西 |
| Mamba 的 A 矩阵在设计时就关注到了让 hidden state 更好的记忆这个问题 | (可能) hidden state 能记得更多 |
| Mamba 让每个位置都用一套不同的参数 | Capacity 更高, (可能) 学习能力更强 |
总结:Mamba 简化了传统 RNN 非线性, 但是增加了其参数量和复杂度
未来展望:
- Mamba 底层理论复杂,不太具备返璞归真的数学美感
- Mamba 架构无疑具备一定的创新性,但实际潜力不明
- Mamba 是站在巨人的肩膀上,揉合了很多前人的智慧
- Mamba 需要一款表现经验的大模型来展示其真正魅力
MambaOut 一文针对 Mamba 的适用性进行分析,并认为 Mamba 的机制非常适合具有长序列和自回归特性的任务。但对部分不符合长序列或自回归特性的图像任务(比如图像分类),Mamba 的表现通常不如卷积和基于注意力的模型(剔除 SSM 模块后反而性能有所提升)
Mamba 原作者在 2024 年 5 月底发表了 Mamba-2 新架构,该论文提出一个叫结构化状态空间二元性(Structured State Space Duality,SSD)的理论框架,将 Transformer 中的注意力机制与 SSM 进行了统一(都可以表示成可半分离矩阵 Semiseparable Matrices 的变换)。同时基于 SSD 思想的新算法,Mamba-2 引入了很多 Transformer 架构的优化方法,使得最终的 Mamba-2 训练更快,性能更强 ——对 Mamba2 感兴趣的话也推荐阅读官方出品的 Mamba2 系列博客
基于 Mamba 框架的衍生模型:
- 2024-04-02 SPMamba:基于双向 SSM 的语音分离,适合长序列音频
- 2024-05-08 StyleMamba :基于 SSM 的文本驱动高效图像风格迁移框架
- 2024-05-23 DiM:Mamba 的效率+扩散模型的表达能力,生成高分辨率图像
- 2024-05-24 Meteor:借助 Mamba 理解多面性信息,构建大型语言和视觉模型
- 2024-05-26 Zamba:7B 的 SSM 和 transformer 混合模型,提高长序列处理能力
- 2024-05-30 DeMamba:用 SSM 捕捉多区域的时空不一致性,实现 AI 视频检测
- 2024-05-30 MSSC-BiMamba:基于双向 SSM 的睡眠监测(PSG)和睡眠障碍诊断
- 2024-06-05 Audio Mamba:纯粹基于 SSM 的音频分类模型,处理长音频更高效
- 2024-07-10 MambaVision:重新设计混合 Mamba-Transformer 的视觉基础模型