1 深度学习基础
2 图神经网络的难点
图数据的复杂性：
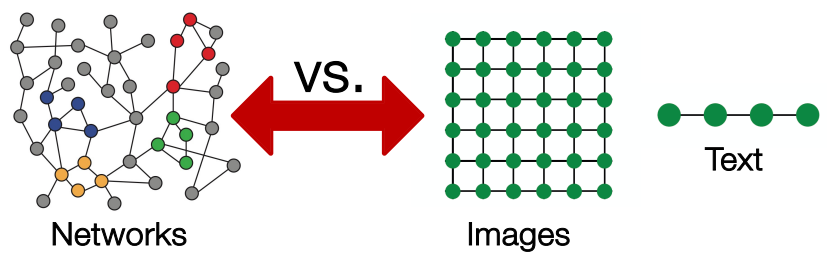
- 存在任意大小和复杂的拓扑结构（不存在网格那样的空间局部性）
- 没有固定的节点顺序或参考点；通常是动态的并且具有多模式特征
直接将邻接矩阵或节点特征输入到传统神经网络的问题：
- $O(|V|)$ 级参数量，难以适用节点数较多的网络
- 无法适用不同尺寸的图/网络，传统网络对节点顺序敏感
置换不变性 vs 置换等价性
- 如果 $f(T(x))=f(x)$，则函数 $f(x)$ 对于转换 $T$ 是不变的（invariant）
- 如果 $f(T(x))=Tf(x)$，则函数 $f(x)$ 对于转换 $T$ 是等价的（equivariant）
- 图数据没有固定的节点顺序，因此需要图函数 $f$ 支持置换不变性
- 传统神经网络（MLP）不具备置换不变性或置换等价性
置换不变性（permutation invariant）的定义：
- 对于图 $G=(A,X)$，图函数 $f$ 需要满足下式才具备置换不变性
$$ f(A,X)=f(PAP^T,PX),f:\mathbb{R}^{|V|\times m}\times \mathbb{R}^{|V|\times|V|}\to\mathbb{R}^d $$
- 其中 $P$ 表示任意的输入排列方式，$d$ 表示节点的嵌入表示维度
同理，图函数 $f$ 需要满足下式才具备置换等价性（permutation equivariant） $$ Pf(A,X)=f(PAP^T,PX),f:\mathbb{R}^{|V|\times m}\times \mathbb{R}^{|V|\times|V|}\to\mathbb{R}^d $$
当图函数 $f$ 将图映射到向量时，一般要求 $f$ 具备置换不变性
当图函数 $f$ 将图映射到矩阵时，一般要求 $f$ 具备置换等价性
3 图神经网络入门
CNN 具备平移不变性：树上的一片叶子落到地上，它还是一片叶子
图神经网络的思考与诞生：
- 受 CNN 启发，考虑从节点及其邻节点中融合信息来构建节点的表征
- 每个节点的邻域定义了一个独特的计算图，描述了图中信息的传播过程
- 考虑使用神经网络来聚合邻节点的信息，基于邻域信息生成节点的嵌入
- 所有节点在网络的每一层都有嵌入表示，其中第 0 层即节点本身的特征
- 网络第 k 层的嵌入表示会从节点的 k 跳邻节点中获取并聚合信息
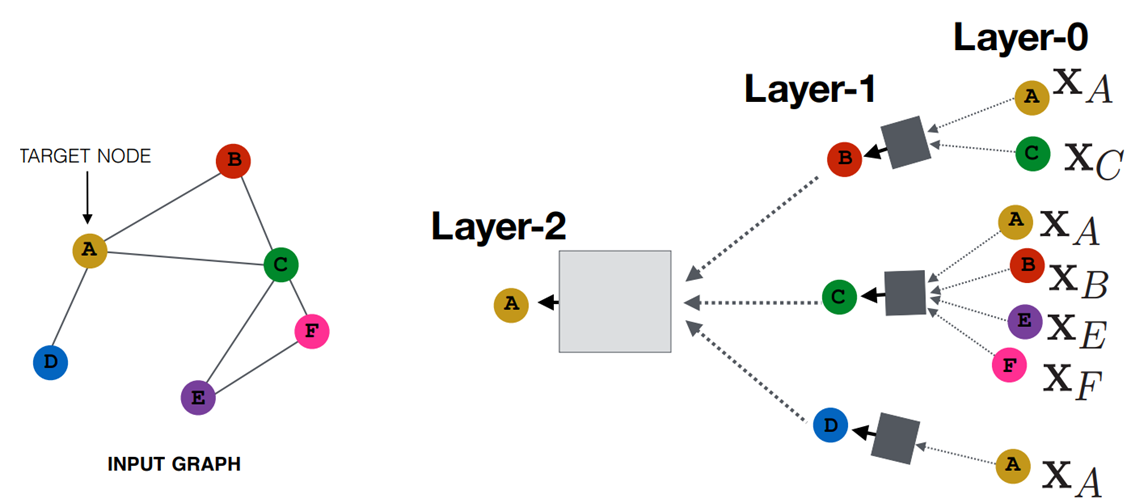
考虑使用"Average"作为邻域信息聚合方式，则 K 层图神经网络的定义如下：
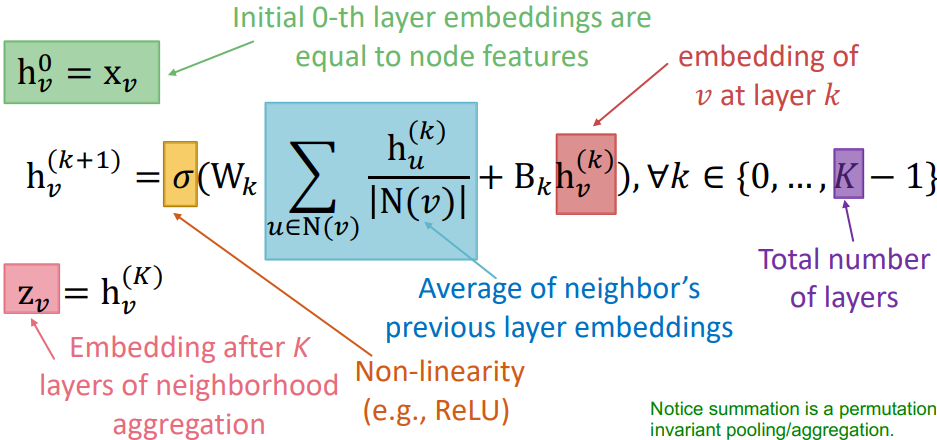
- 上式中，第一项（蓝）是对邻域信息的转换和聚合，第二项（橙）是对节点历史信息的再加工
- 使用输入的节点特征作为第 0 层的节点嵌入（初始化），最终的节点嵌入表示来自第 K 层输出
- 图神经网络实现了参数共享，即每个节点生成嵌入表示时共享可训练参数 $W_k$ 和 $B_k$
图神经网络的置换不变性与置换等价性
- 图神经网络用"Average"来聚合邻域信息，同时不同节点共享神经网络权重
- 所以网络满足置换不变性（每个节点的嵌入表示不会因为输入节点顺序调整而改变）
- 网络输入的节点特征与输出的嵌入是行对齐的，同时每个节点嵌入满足置换不变性
- 所以网络满足置换等价性（调整输入的节点特征顺序后，对应的节点嵌入保持不变）
4 训练图神经网络
前置知识：邻接矩阵A和度矩阵D
将图神经网络的定义（单层）转化为矩阵形式： $$ \begin{aligned}&H^{(k+1)}=\sigma(\tilde{A}H^{(k)}W_k^\mathrm{T}+H^{(k)}B_k^\mathrm{T}) \\&\mathrm{where}\quad\tilde{A}=D^{-1}A\end{aligned} $$
其中矩阵 $\tilde{A}$ 是稀疏的，可以通过稀疏矩阵运算进行加速
对于无监督训练，考虑使用图结构作为监督（类似上一节中图嵌入的做法） $$ \min_\Theta\mathcal{L}=\sum_{z_u,z_v}\mathrm{CE}(y_{u,v},\mathrm{dot}(f_{\Theta}(u),f_{\Theta}(v))) $$
- 核心思想：依然是“相似”的节点应该具有相似的嵌入
- 当节点 $u$ 和节点 $v$ 相似（共现概率高）时，$y_{u,v}=1$
- 上式中，$f_{\Theta}$ 表示网络编码，$dot$ 表示点积函数，$CE$ 表示交叉熵损失
对于有监督训练（如节点分类），可以直接定义损失函数（如交叉熵）：
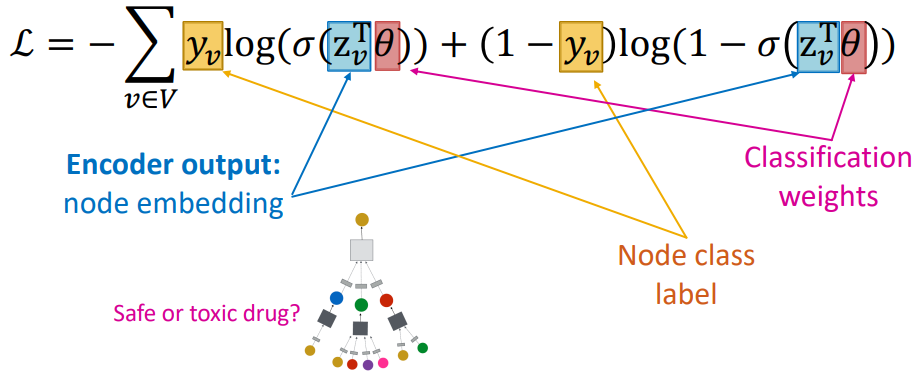图神经网络的训练过程小结：
- 定义邻域聚合函数
- 定义嵌入的损失函数
- 在一组节点（计算图）上进行训练
- 根据需要生成节点的嵌入表示
图神经网络实现了归纳式学习（inductive learning），能为训练过程中未见过的节点生成嵌入表示
5 对比传统神经网络
GNN vs CNN：
- CNN 在计算形式上 GNN 存在相似之处，可以看作一种特殊的GNN
- CNN 的领域大小和输入排序是固定的，GNN 则不是固定的（更加灵活）
- CNN 的滤波器/卷积核参数需要学习，GNN 的卷积核参数则来自图结构
- CNN 不满足置换不变性和置换等价性，而 GNN 满足
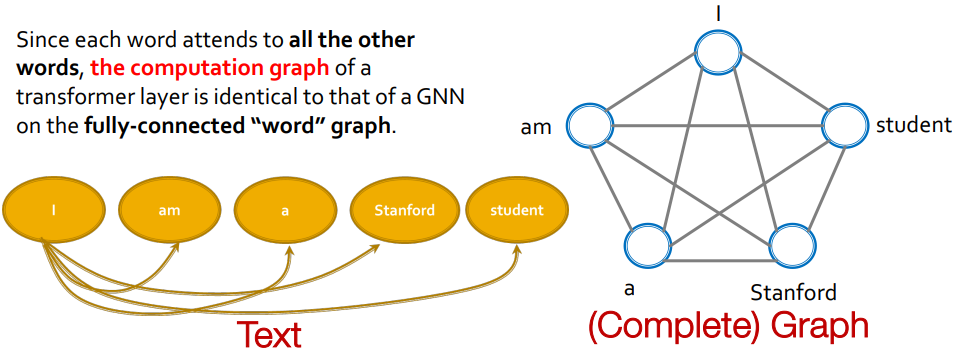
Transformer ：10.《动手学深度学习》注意力机制
Transformer 可以看作是一个构造在全连接词图上的 GNN：
