卷积神经网络(CNN):引入了卷积操作的神经网络
普通卷积
严格来说,卷积层是个错误的叫法,因为它所表达的运算其实是互相关运算(cross-correlation)
二维互相关运算示例:
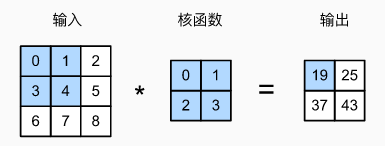
汇聚/池化层
池化(pool)层的优点:降低卷积层对位置的敏感性
常用池化层分两种:最大池化层和平均池化层,前者示例如下:

类似于卷积层,池化层也会有填充和步幅,使用大于 1 的步幅可以起到降维的作用
不同于卷积层,池化层在每个输入通道上是单独计算的,所以池化层的输出通道数等于输入通道数
膨胀卷积
膨胀(dilated)卷积,也称空洞卷积,扩展卷积
其主要作用是在不增加参数和模型复杂度的条件下,可以指数倍的扩大视觉野
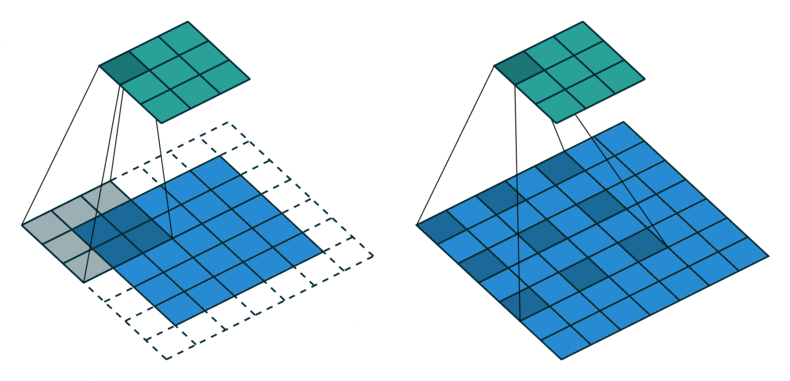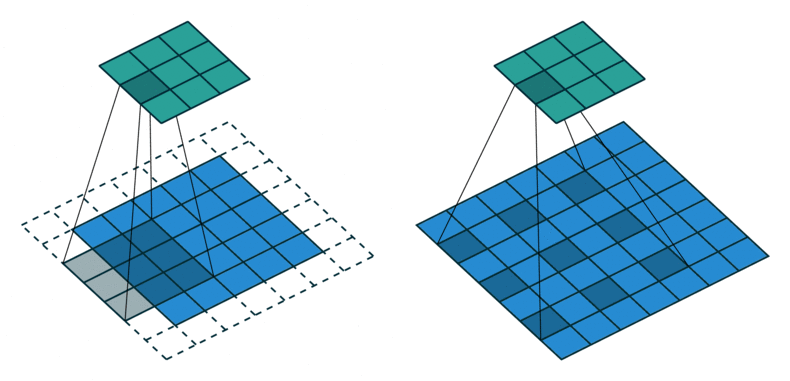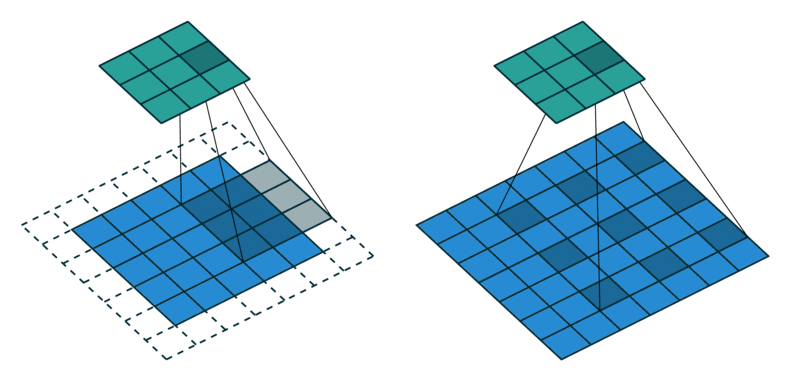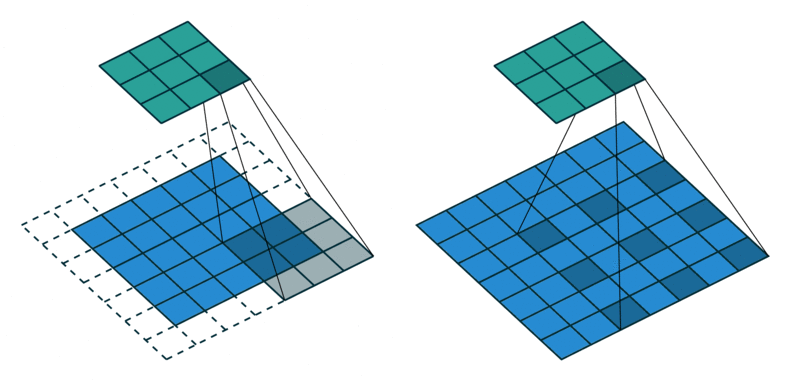
普通卷积(左) vs 膨胀卷积(右)
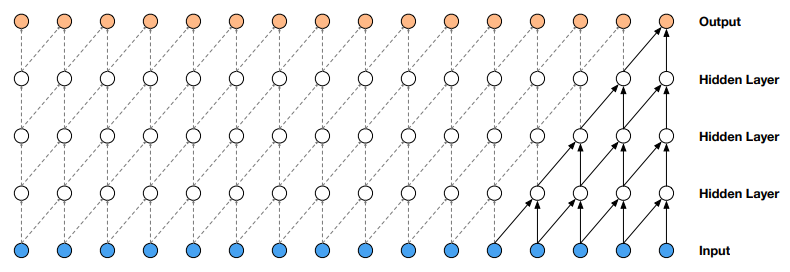
因果卷积
因果卷积主要改善了普通卷积无法处理时序问题的情况
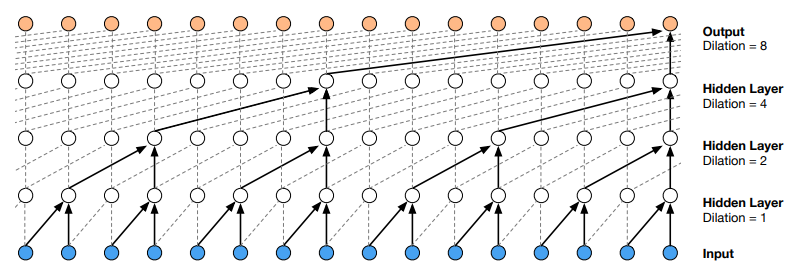
因果卷积还可以配置膨胀卷积使用,以处理更长的时序数据:
转置卷积
正常情况下的卷积常使用下采样的方式减少输出图像的维度(高宽),而某些应用场景(比如像素级分类-语义分割)需要保持输出维度和输入维度相同。因此提出转置卷积,通过类似上采样的思路来维持或增大输出的维度
一个步幅为 1 的 $2\times 2$ 转置卷积 (Transpose Convolution)示例如下 :

转置卷积中“转置”的含义
假设输入维度为 $(h,w)$,经过卷积操作后变为 $(h',w')$。则同样超参设定的转置卷积操作,可以将维度为 $(h',w')$ 的输入转化维度为 $(h,w)$。二者在维度转换方面是一个“互逆”的过程。
注意概念区分:卷积在数学上的严格逆运算是反卷积 (deconvolution),此运算很少在深度学习中使用,通常意义中的反卷积神经网络是指使用了转置卷积的神经网络
图卷积
图卷积的核心思想是利用边的信息对节点信息进行聚合从而生成新的节点表示
具体实现可参考 GCN_谱图卷积