GCN_基于图卷积网络的半监督学习
发表评论
649 views

中文标题：GCN_基于图卷积网络的半监督学习

英文标题：Semi-Supervised Classification with Graph Convolutional Networks

发布平台：ICLR

ICLR

发布日期：2016-09-09

引用量（非实时）：22641

DOI：10.48550/arXiv.1609.02907

作者：Thomas N. Kipf, Max Welling

关键字： #GCN #半监督

文章类型：journalArticle

品读时间：2023-02-15 0:08

1 文章萃取

1.1 核心观点

  • 本文提出了一种用于图结构数据的半监督学习方法GCN，该方法在图的傅里叶变换基础上进行优化，通过卷积的一阶近似、参数量约束、邻近矩阵的归一化等技巧增强了图卷积模型的稳定性和可拓展性，使得最终模型合理地利用到有监督信息和图结构信息。GCN模型的计算复杂度和存储成本随着图的边数线性递增，并在实验阶段表现出性能和运算上的优越性

1.2 综合评价

  • 原文不长但信息量很大，需要补充很多前置知识
  • 本文具有极强开创性，实现了卷积在图结构中的可行方案
  • 本文的精华部分在于模型逐步优化的思路，很值得精读
  • 本笔记部分符号使用与原文存在部分出入

1.3 主观评分：⭐⭐⭐⭐⭐

2 精读笔记

2.1 背景知识与损失函数

理解图论基本概念和拉普拉斯矩阵：图论基础

理解傅里叶变换和卷积定理的基本概念： 傅里叶变换

基于图的半监督学习：对图中的节点进行分类，图中只有部分节点是有标签的

此类任务的常用损失函数： $$L=L_0+\lambda L_{reg}\ \ ,\ \ L_{reg}=\Sigma_{i,j}A_{i,j}||f(X_i)-f(X_j)||^2=f(X)^T\Delta f(X)$$

  • 其中$L_o$表示带标签部分节点对应的有监督损失
  • $L_{reg}$表示基于图结构得到的拉普拉斯正则项，$\lambda$为正则项权重参数
  • $A$表示邻接矩阵，当节点$i$和节点$j$存在关联时$A_{ij}=1$，否则$A_{ij}=0$
  • $D$表示度矩阵（$D_{ii}=\Sigma_j A_{ij}$），$\Delta$表示拉普拉斯矩阵（$\Delta=D-A$）
  • 拉普拉斯正则项约束相邻的节点对应的目标函数值$f$应该是相似的

拉普拉斯正则项使得模型能够自动学习并利用到图的结构信息

其他常见的图表示学习方法：

  • 受skip-gram模型启发，DeepWalk利用随机游走+节点邻域信息来构建节点的嵌入
  • LINE和node2vec在DeepWalk的基础上进行了搜索策略的改进
  • 有些研究者在图神经网络的训练有引入RNN或卷积的机制，但都存在局限性
  • 还有人将局部图转化为序列，以便更好地使用常规一维卷积网络进行处理

Bruna等人首次引入了频谱图卷积神经网络，而Defferard 等人使用快速局部卷积进行扩展。在此基础上，本文提出的图卷积神经网络（GCN）对前者的框架进行简化，再加上适当的归一化处理，极大提高了网络的可伸缩性和性能

2.2 图的快速近似卷积

定义图卷积神经网络的（单层）形式： $$H^{(l+1)}=\sigma(\widetilde{D}^{-1/2}\widetilde{A}\widetilde{D}^{-1/2}H^{(l)}W^{(l)})$$

  • 其中$H^{(l)}$为第$l$层网络的输入（初始输入为$H^{(0)}=X$），$W^{(l)}$为第$l$层的待训练参数
  • $\widetilde{A}=A+I_N$为添加了自环（自连接）的邻接矩阵，相应的度矩阵为$\widetilde{D}$，$\widetilde{D}{ii}=\Sigma_j \widetilde{A}{ij}$
  • $\sigma$为第$l$层的激活函数，$H^{(l+1)}$为第$l$层网络的输出，也是第$l+1$层网络的输入

本小节后面将具体介绍这个公式是怎么推导出来的

2.2.1 谱图卷积

阅读本小节前请先了解图的傅里叶变换的基本内容

对拉普拉斯矩阵$\Delta$进行特征分解，可得到特征向量矩阵$U$和特征值向量$\Lambda$

给定信号$x$（一般为图节点的特征向量）和卷积核$g$，二者在图域的卷积可转化为傅里叶域的相乘： $$g\ast x=U(U^Tg \odot U^Tx)=Ug_{\theta}U^Tx$$

  • 其中$g_{\theta}$是拉普拉斯矩阵特征值$\Lambda$的函数：$g_{\theta}(\Lambda)=U^Tg$
  • $\theta$是函数$g_{\theta}$的参数，在本文中可定义：$g_{\theta}(\Lambda)=diag(\theta)$
  • 所以$g_{\theta}$其实可看作傅里叶域的卷积核的对角矩阵形式

上式中$U$的得出需要经过计算复杂度为$O(N^2)$的特征分解，计算成本较高

为了解决这一问题，考虑借助切比雪夫（Chebyshev）多项式的前$K$项展开来近似卷积核： $$g_{\theta}(\Lambda) \approx \Sigma_{k=0}^{K}\beta_k T_k(\widetilde{\Lambda})$$

  • 其中$T_k$为$k$阶的切比雪夫多项式；$\beta_k$为多项式系数，也是待训练参数
  • 切比雪夫多项式要求输入取值在$[-1,1]$之间，所以对$\Lambda$进行标准化处理：$\widetilde{\Lambda}=2\Lambda/\lambda_{max}-I$，其中$\lambda_{max}$表示拉普拉斯矩阵的最大特征值；实际操作时，则是对拉普拉斯矩阵进行标准化处理：$\widetilde{L}=2\Delta/\lambda_{max}-I$
  • 此近似计算得到的是K-局部卷积核，即只考虑每个节点K步以内的邻域节点

将$g_{\theta}$的切比雪夫多项式近似带入最开始的卷积运算中： $$g\ast x=Ug_{\theta}U^Tx=U\Sigma_{k=0}^{K}\beta_k T_k(\widetilde{\Lambda})U^Tx=\Sigma_{k=0}^{K}\beta_k T_k(\widetilde{L})x$$

切比雪夫多项式递归定义为$T_k(x)=2xT_{k-1}(x)-T_{k-2}(x),T_0=1,T_1=x$；

选择切比雪夫多项式的好处：

  • 满足正交基的多项式（无共线性+拟合能力）
  • 降低计算量（系数拟合方便，避免了特征分解）
  • 保证数值稳定（切比雪夫多项式的值域限定在[-1,1]之间）
  • 其他更多原因有待进一步发掘~
2.2.2 分层线性模型

上一节描述了一个卷积层的运算过程，而多个卷积层的堆叠便得到了基于图卷积的神经网络模型

假设卷积运算中的K=1（用线性函数来近似卷积核），此时每个节点的卷积运算只考虑其邻接节点，这种做法能够缓解图局部邻域结构引发的过拟合问题，也可以在有限的算力下建立层次更深的网络结构： $$g\ast x \approx \Sigma_{k=0}^{1}\beta_k T_k(\widetilde{L})x=\beta_0x+\beta_1\widetilde{L}x$$ 当K=1时，归一化拉普拉斯矩阵的特征值范围为[0,2]，因此可假定$\lambda_{max}=2$

（对称型）归一化拉普拉斯矩阵可表示如下： $$\Delta_{new}=D^{-1/2}\Delta D^{-1/2}=D^{-1/2}(D-A) D^{-1/2}=I-D^{-1/2}A D^{-1/2}$$

将上式代入$\widetilde{L}$并化简：$\widetilde{L}=2\Delta/\lambda_{max}-I=-D^{-1/2}A D^{-1/2}$

将上式代入$g\ast x$并化简：$g\ast x =\beta_0x+\beta_1\widetilde{L}x=\beta_0x-\beta_1D^{-1/2}A D^{-1/2}x$

通过限制参数量来进一步减少运算量并缓解过拟合，令$w=\beta_0=-\beta_1$可得： $$g\ast x =\beta_0x-\beta_1D^{-1/2}A D^{-1/2}x\approx w(I_N+D^{-1/2}A D^{-1/2})x$$ 注意到$I_N+D^{-1/2}A D^{-1/2}$的特征值范围在[0,2]之间，当网络层次较深时反复使用该算子容易导致数值不稳定和梯度爆炸/消失。所以使用归一化技巧：$\widetilde{A}=A+I_N$，相应的度矩阵为$\widetilde{D}$，$\widetilde{D}{ii}=\Sigma_j \widetilde{A}{ij}$

$\beta_0x$是对当前节点输入特征的计算，$\beta_1D^{-1/2}A D^{-1/2}x$是对邻接节点输入特征的计算；$\widetilde{A}=A+I_N$为添加了自环（自连接）的邻接矩阵，使得原本两部分的计算可以通过一个矩阵实现

代入归一化后的$\widetilde{A}$和$\widetilde{D}$后，卷积运算可化简如下： $$g\ast x =w(I_N+D^{-1/2}A D^{-1/2})x=\widetilde{D}^{-1/2}\widetilde{A}\widetilde{D}^{-1/2}wx$$ 加上激活函数后，就可以得到最初定义的图卷积神经网络的（单层）形式： $$H^{(l+1)}=\sigma(\widetilde{D}^{-1/2}\widetilde{A}\widetilde{D}^{-1/2}H^{(l)}W^{(l)})$$

2.3 半监督的节点分类

令$\hat{A}=\widetilde{D}^{-1/2}\widetilde{A}\widetilde{D}$，考虑一个简单双层图卷积神经网络处理多分类问题： $$Z=f(X,A)=softmax(\hat{A}ReLU(\hat{A}XW^{(0)})W^{(1)})$$

  • 其中输入为$X\in R^{N\times C}$，第1层参数矩阵$W^{(0)}\in R^{C\times H}$，第2层参数矩阵$W^{(1)}\in R^{H\times F}$
  • 矩阵$A$使用稀疏表示，内存需求为$O(|\epsilon|)$，其中$|\epsilon|$表示图中边的数量
  • 使用GPU高效实现了稀疏矩阵乘法，所以神经网络的整体计算复杂度为$O(|\epsilon|CHF)$
  • 针对该问题，使用交叉熵作为有监督学习部分的损失度量

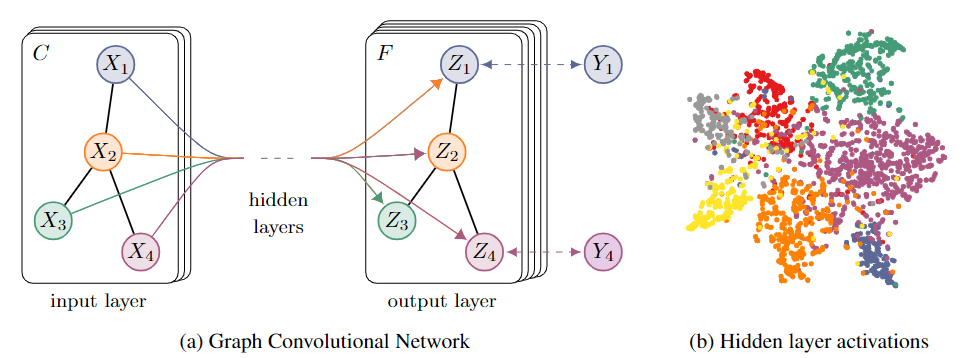
  • 上图中左侧为图卷积神经网络的简单结构说明
  • 上图中右侧通过T-SNE算法对数据集及其标签进行可视化

2.4 实验分析

实验使用数据：三个引文网络数据集 Citeseer、Cora 和 PubMed 和一个知识图网络 0_life/精品资源/数据资源/知识图数据资源#NELL

实验细节补充：

  • 将引用链接视为（无向）边来构造图，并计算二元对称邻接矩阵A
  • 每个文档都有一个类标签，但在训练时每个类只使用20个标签（模拟半监督场景）
  • 保留500个样本用于验证集调参，保留1000个样本用于测试集评估准确率
  • 学习率为0.01，最大训练次数为200，早停（early-stopping）为10，其他超参略

不同算法的分类准确率对比：

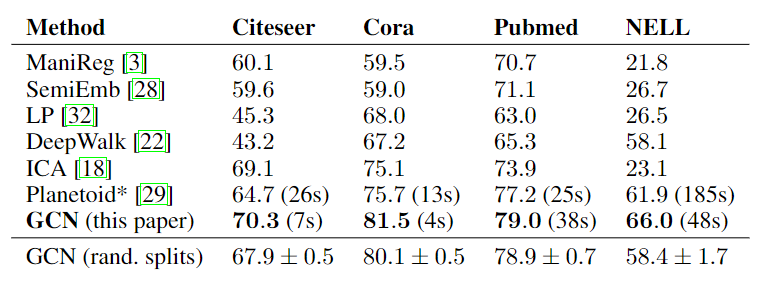
  • 以上结果为随机初始化重复100次后的平均分类精度

不同滤波器的结果对比：

  • 使用切比雪夫不等式1阶近似（$1^{st}$-order）效果略低于2-3阶近似
  • 限制参数量（Single parameter）能很好地提高模型的表现
  • 邻接矩阵添加自环（自连接）的归一化技巧能显著提高模型的表现

每轮模拟的平均训练时间（前向传递、交叉熵计算、后向传递），星号表示内存不足：

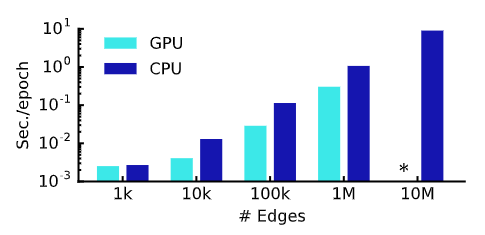
模型分析：

  • 基于GCN的神经网络在分类性能最优的情况下还保持着较好的运算效率
  • 内存需求随着数据集的大小线性增长，难以处理存在密集连接的大型图数据集
  • 目前的GCN仅支持无向图，考虑邻域的信息时主要受到超参K的调控
  • 对于深度超过7层的GCN模型，不使用残差连接的训练可能会变得困难

相关资源

往年同期文章