遗传算法(Genetic Algorithm, GA)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。
遗传算法的关键要素:
- 种群(population)代表问题可能潜在的解集的一个开始的
- 一个种群由经过基因(gene)编码的定数目的个体(individua)组成
核心过程:
- 编码:实现从表现型到基因型的映射,同时构建初代种群
- 选择:在每一代,根据问题域中个体的适应度(fitness)选择个体
- 变异:借助于遗传学算子(genetic operators)进行组合交叉和变异,产生代表新解集的种群
- 演化:按照适者生存和优胜劣汰的原理,逐代(generation)演化产生出更好的近似解
- 终止:末代种群中的最优个体经过解码(decoding),作为问题近似最优解返回
三个基本操作
- 选择:假设适应度函数为$f$,则种群中所有个体的适应度之和为$F=\Sigma_{k=1}^nf(X_k)$;则第$k$个个体被选中并遗传到下一代种群中的概率为$p_k=f(X_k)/F$
- 交叉:对种群中的个体进行两两随机配对,针对每一对已配对个体(父代),随机选择交叉点,并相互交互两个个体的基因信息,从而产生两个新的个体(子代)
- 变异:最简单的单点变异算子就是在生成子代个体时,随机选择部分基因进行改变
根据数据编码方式的不同,变异操作也会存在一定的差异
对于浮点型编码,变异操作常使用数据重抽样或偏移等调整方法 对于整数型编码,变异操作常使用位置互换或符号取反等调整方法
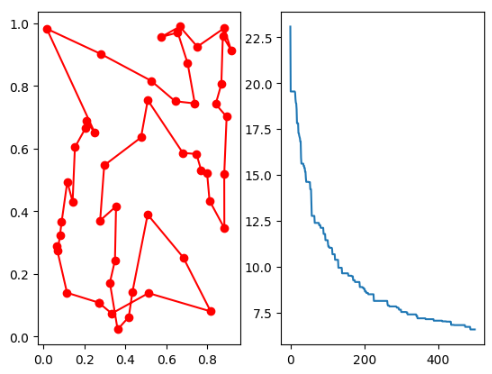
基于scikit-opt包的Python实现——解决旅行商问题:
import numpy as np
from scipy import spatial
import matplotlib.pyplot as plt
num_points = 50
# 随机生成距离矩阵
points_coordinate = np.random.rand(num_points, 2) # generate coordinate of points
distance_matrix = spatial.distance.cdist(points_coordinate, points_coordinate, metric='euclidean')
def cal_total_distance(routine):
'''The objective function. input routine, return total distance.
cal_total_distance(np.arange(num_points))
'''
num_points, = routine.shape
return sum([distance_matrix[routine[i % num_points], routine[(i + 1) % num_points]] for i in range(num_points)])
from sko.GA import GA_TSP
ga_tsp = GA_TSP(func=cal_total_distance, n_dim=num_points, size_pop=50, max_iter=500, prob_mut=1)
best_points, best_distance = ga_tsp.run()
fig, ax = plt.subplots(1, 2)
best_points_ = np.concatenate([best_points, [best_points[0]]])
best_points_coordinate = points_coordinate[best_points_, :]
ax[0].plot(best_points_coordinate[:, 0], best_points_coordinate[:, 1], 'o-r')
ax[1].plot(ga_tsp.generation_best_Y)
plt.show()