1 基本概念
粒子群优化(particle swarm optimization,PSO)算法是计算智能领域的一种群体智能的优化算法(其他群体算法举例:蚁群算法,鱼群算法等),该算法最早由Kennedy和Eberhart在1995年提出的,该算法源自对鸟类捕食问题的研究。
鸟类捕食的生物过程:
- 假设一群鸟在觅食,在觅食范围内,只在一个地方有食物
- 所有鸟儿都看不到食物(即不知道食物的具体位置。当然不知道了,知道了就不用觅食了),但是能闻到食物的味道(即能知道食物距离自己是远是近。鸟的嗅觉是很灵敏的)
- 假设鸟与鸟之间能共享信息(即互相知道每个鸟曾经离食物多远),那么最好的觅食策略就是结合自己离食物最近的位置和鸟群中其他鸟距离食物最近的位置这2个因素以找到最好的搜索区域
粒子群算法的关键要素
- 粒子(particle)和种群(population):一只鸟和一群鸟
- 位置(position)和速度(velocity ):一个粒子(鸟)当前所在的位置/速度
- 经验(best):一个粒子(鸟)自身曾经离食物最近的位置
- 适应度(fitness):一个粒子(鸟)距离食物的远近
2 核心过程
PSO算法核心过程:
- 可行解空间中初始化一群粒子,每个粒子都代表极值优化问题的一个潜在最优解,用位置$X$、速度$V$和适应度值$P$三项指标表示该粒子特征
- 粒子在解空间中运动,通过跟踪个体极值$P_{best}$(个体所经历的适应度值最优位置)和群体极值$G_{best}$(种群中的所有粒子所经历的适应度值最优位置)更新个体位置
- 粒子每更新一次位置,就计算一次适应度值,个体极值$P_{best}$和群体极值$G_{best}$通过与新粒子的适应度值比较,来实现个体极值、群体极值的适应度值和位置的更新
当迭代次数为$k$时,PSO算法中第$i$个粒子速度和位置的更新公式如下: $$\begin{equation} \left\{ \begin{gathered} V_i^{k+1}=\omega V_i^k+c_1r_1(P_i^k-X_i^k)+c_2r_2(P_g^k-X_i^k) \ \\ X_i^{k+1}=X_i^k+V_i^k \end{gathered} \right. \end{equation}$$
- 其中$k+1$时刻的个体速度$V_i^{k+1}$取决于:(1)上一时刻的速度$V_i^k$;(2)当前位置$X_i^k$与历史最优个体位置$P_i^k$的偏差;(3)当前位置$X_i^k$与群体全局的历史最优位置$P_g^k$的偏差
- 系数$\omega$描述了PSO算法的速度更新惯性,较小的惯性因子意味着算法的随机性更强
- $c_1$和$c_2$为超参数;$r_1$和$r_2$表示在0~1之间服从均匀分布的随机数,对应算法的随机性
3 算法分析
参数常见取值:
- 粒子数:一般取值在20~40之间,值越大对应的粒子数越多,搜索范围和复杂度越高
- 惯性因子$\omega$:常见取值在0.6~0.75之间;较大时有利于全局搜索,较小时有利于局部搜索;一个经验做法是使用线性递减惯性权重(LDIW)法,随着迭代次数将$\omega$从0.9线性递减到0.4
- 超参数 $c_1$和$c_2$:常见取值在1.5~2之间,可用于调控对于自身经验和群体经验的侧重
与遗传算法(GA)的对比:
- 共同点是都需要实现种群的初始随机化和适应度函数的定义
- PSO算法没有选择/交叉/变异等操作算子,但具备记忆功能
- GA的个体间是信息共享的,种群在迭代过程是比较均匀地向最优区域移动
- PSO只会单向传送个体/群体的最优信息,迭代过程会跟随当前最优解(收敛快)
4 代码实现
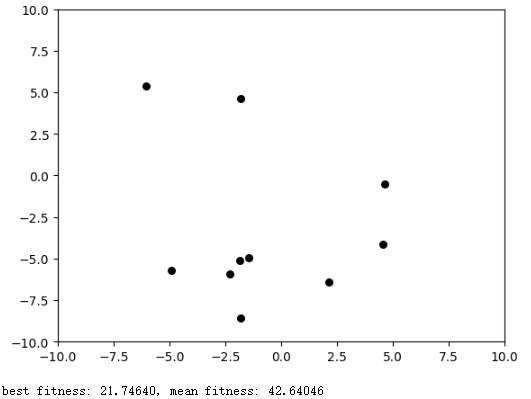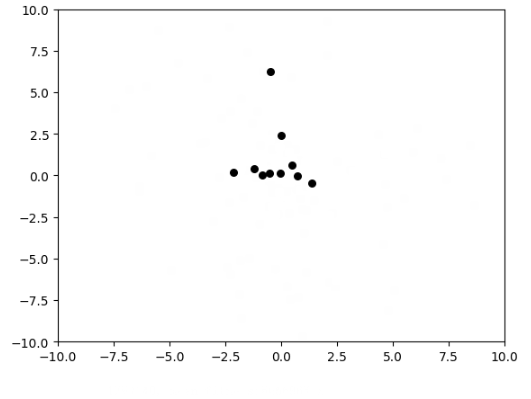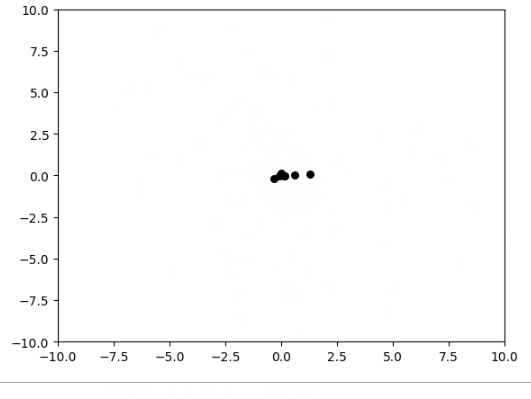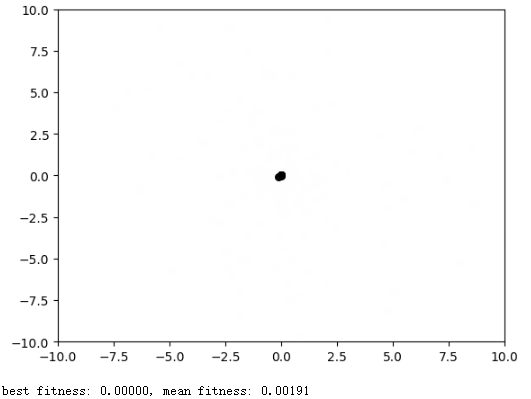
使用粒子群算法寻找函数$f(x_1,x_2)=x_1^2+x_2^2$的最小值
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
from IPython import display
# 参考链接:https://blog.csdn.net/winycg/article/details/79120154
class PSO(object):
def __init__(self, population_size, max_steps):
self.w = 0.6 # 惯性权重
self.c1 = self.c2 = 2
self.population_size = population_size # 粒子群数量
self.dim = 2 # 搜索空间的维度
self.max_steps = max_steps # 迭代次数
self.x_bound = [-10, 10] # 解空间范围
self.x = np.random.uniform(self.x_bound[0], self.x_bound[1],
(self.population_size, self.dim)) # 初始化粒子群位置
self.v = np.random.rand(self.population_size, self.dim) # 初始化粒子群速度
fitness = self.calculate_fitness(self.x)
self.p = self.x # 个体的最佳位置
self.pg = self.x[np.argmin(fitness)] # 全局最佳位置
self.individual_best_fitness = fitness # 个体的最优适应度
self.global_best_fitness = np.max(fitness) # 全局最佳适应度
def calculate_fitness(self, x):
return np.sum(np.square(x), axis=1)
def evolve(self):
fig = plt.figure()
for step in range(self.max_steps):
r1 = np.random.rand(self.population_size, self.dim)
r2 = np.random.rand(self.population_size, self.dim)
# 更新速度和权重
self.v = self.w*self.v+self.c1*r1*(self.p-self.x)+self.c2*r2*(self.pg-self.x)
self.x = self.v + self.x
plt.clf()
plt.scatter(self.x[:, 0], self.x[:, 1], s=30, color='k')
plt.xlim(self.x_bound[0], self.x_bound[1])
plt.ylim(self.x_bound[0], self.x_bound[1])
display.clear_output(wait=True)
plt.pause(0.01)
fitness = self.calculate_fitness(self.x)
# 需要更新的个体
update_id = np.greater(self.individual_best_fitness, fitness)
self.p[update_id] = self.x[update_id]
self.individual_best_fitness[update_id] = fitness[update_id]
# 新一代出现了更小的fitness,所以更新全局最优fitness和位置
if np.min(fitness) < self.global_best_fitness:
self.pg = self.x[np.argmin(fitness)]
self.global_best_fitness = np.min(fitness)
print('best fitness: %.5f, mean fitness: %.5f' % (self.global_best_fitness, np.mean(fitness)))
pso = PSO(10, 100)
pso.evolve()