1 注意力提示
“注意力经济”时代:人类的注意力被视为可以交换的、有限的、有价值的且稀缺的商品。各种流媒体和游戏都在努力吸引消耗人类的注意力,因为这都是流量,都是能转换为金钱的存在。
现实视觉世界中,注意力的用于符合双组件(two-component)框架,既包含自主性提示(volitional cue,比如阅读时,注意力会自主集中在书本上),也包含非自主性提示(nonvolitional cue,比如当一面白墙上存在一幅彩绘时,注意力会不自主地集中过去)
传统的神经网络层(比如全连接层或池化层)都是简单地对输入的内容(非自主性提示)进行直接处理并抽取特征;而注意力机制的优势在于引入了查询(query,一种自主性提示),进而主动地对输入的键(非自主性提示)进行引导(注意力池化,attention pooling),从而得出更合理的值(融入了主观倾向性)用于输入,这种引导和注意力的主动集中过程非常相似
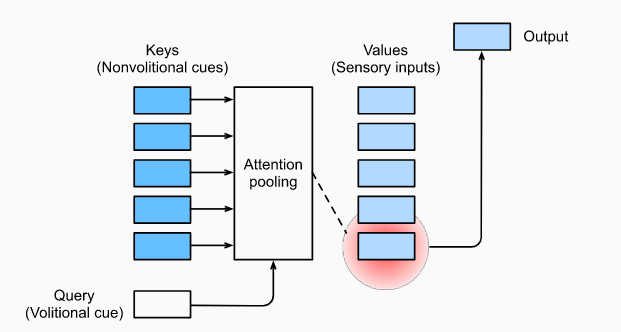
2 注意力池化:Nadaraya-Watson 核回归
查询(自主提示)和键(非自主提示)之间的交互形成了注意力池化,注意力池化对值(感官输入)进行有选择地聚合以生成最终的输出。
1964年提出的Nadaraya-Watson核回归模型是具有注意力机制的机器学习范例,本小节将围绕这一模型探讨注意力池化的更多细节
给定训练集为$(x_i,y_i),i=1,...,n$,则一个简单的估计器是平均池化: $$f(x)=\frac{1}{n}\Sigma_iy_i$$ 而Nadaraya-Watson核回归模型可以表示如下: $$f(x)=\Sigma_{i=1}^n\frac{K(x-x_i)}{\Sigma_{j=1}^nK(x-x_j)}y_i$$ 其中$K$表示一种核函数,比如高斯核(Gaussian kernel)的形式可表示如下: $$K(u)=\frac{1}{\sqrt{2\pi}}exp(-\frac{u^2}{2})$$
Nadaraya-Watson核回归模型分析
- Nadaraya-Watson核回归是一个非参模型,没有需要学习的参数
- Nadaraya-Watson核回归本质是一种对$y_i$的加权平均:$f(x)=\Sigma_i \alpha(x,x_i)y_i$
- 模型具有一致性(consistency)的优点: 数据足够多时模型能收敛到最优结果
- 权重即可看作重视程度,也是一种注意力的具体表现
- 分析模型的表达式,$(x,x_j,y_i)$可以理解为是$(query,key,value)$
将$K=$高斯核带入Nadaraya-Watson核回归,即可得到非参数的注意力池化模型: $$f(x)=\Sigma_{i=1}^n\frac{exp(-\frac{1}{2}(x-x_i)^2)}{\Sigma_{j=1}^nexp(-\frac{1}{2}(x-x_i)^2}y_i=\Sigma_{i=1}^nsoftmax(-\frac{1}{2}(x-x_i)^2)y_i$$ 此时模型的预测结果表现如下:
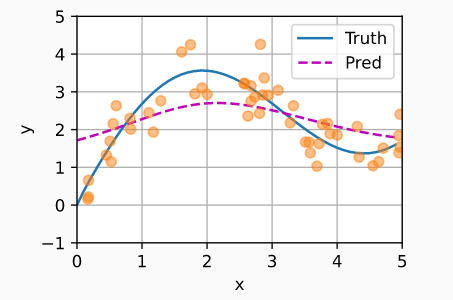
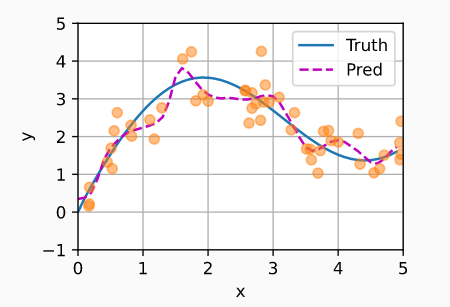
而带参数的注意力池化模型则是在$query$和$key$之间添加了新的可学习参数$w$: $$f(x)=\Sigma_{i=1}^nsoftmax(-\frac{1}{2}((x-x_i)w)^2)y_i$$
此时模型的预测结果表现如下:
3 注意力评分函数
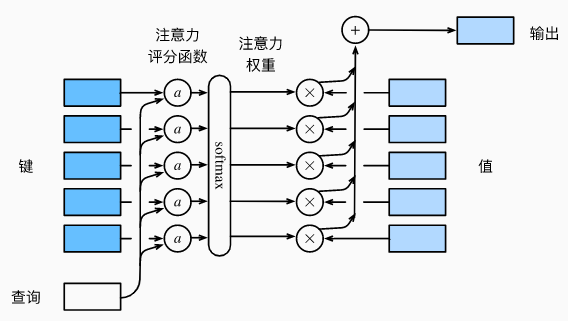
上一节中,注意力池化函数可以实现进一步的抽象/简化: $$f(x)=\Sigma_{i=1}^nsoftmax(-\frac{1}{2}(x-x_i)^2)y_i=\Sigma_i\alpha(x,x_i)y_i$$其中$\alpha$即表示注意力评分函数(attention scoring function), 简称评分函数
注意力池化层函数的输入包括一个查询$q$和$m$个键值对$[(k_1,v_1),...,(k_m,v_m)]$: $$f(q,(k_1,v_1),...,(k_m,v_m))=\Sigma_{i=1}^m\alpha(q,k_i)v_i$$
以Nadaraya-Watson核回归为例,理解上式:
- $q$是每次预测的输入值$x$,$m$个键值对则是历史数据集$[(x_1,y_1),...,(x_m,y_m)]$
- 所以N-W核回归会根据查询$x$,计算$x$与历史数据集的每个样本$x_i$的相似度,并作为权重计算历史样本标签$y_i$的加权平均,并作为H-W核回归的预测输出
对于仅用于填充的无效词元,使用较大的负值替换掉需要被掩码的最终层输出,使其softmax映射结果趋近于0,从而实现softmax掩蔽操作:
基于PyTorch实现掩蔽softmax操作:
#@save
def masked_softmax(X, valid_lens):
"""通过在最后一个轴上掩蔽元素来执行softmax操作"""
# X:3D张量,valid_lens:1D或2D张量
if valid_lens is None:
return nn.functional.softmax(X, dim=-1)
else:
shape = X.shape
if valid_lens.dim() == 1:
valid_lens = torch.repeat_interleave(valid_lens, shape[1])
else:
valid_lens = valid_lens.reshape(-1)
# 最后一轴上被掩蔽的元素使用一个非常大的负值替换,从而其softmax输出为0
X = d2l.sequence_mask(X.reshape(-1, shape[-1]), valid_lens,
value=-1e6)
return nn.functional.softmax(X.reshape(shape), dim=-1)
当查询和键长度不一致时,可以使用加性注意力(additive attention)评分函数: $$a(q,k)=w_v^Ttanh(W_qq+W_kk)$$ 其中的可学习参数包括$W_q\in \mathbb{R}^{h\times q},W_k\in \mathbb{R}^{h\times k},w_v\in \mathbb{R}^{h}$
基于PyTorch实现加性注意力:
#@save
class AdditiveAttention(nn.Module):
"""加性注意力"""
def __init__(self, key_size, query_size, num_hiddens, dropout, **kwargs):
super(AdditiveAttention, self).__init__(**kwargs)
self.W_k = nn.Linear(key_size, num_hiddens, bias=False)
self.W_q = nn.Linear(query_size, num_hiddens, bias=False)
self.w_v = nn.Linear(num_hiddens, 1, bias=False)
self.dropout = nn.Dropout(dropout)
def forward(self, queries, keys, values, valid_lens):
queries, keys = self.W_q(queries), self.W_k(keys)
# 在维度扩展后,
# queries的形状:(batch_size,查询的个数,1,num_hidden)
# key的形状:(batch_size,1,“键-值”对的个数,num_hiddens)
# 使用广播方式进行求和
features = queries.unsqueeze(2) + keys.unsqueeze(1)
features = torch.tanh(features)
# self.w_v仅有一个输出,因此从形状中移除最后那个维度。
# scores的形状:(batch_size,查询的个数,“键-值”对的个数)
scores = self.w_v(features).squeeze(-1)
self.attention_weights = masked_softmax(scores, valid_lens)
# values的形状:(batch_size,“键-值”对的个数,值的维度)
return torch.bmm(self.dropout(self.attention_weights), values)
当查询和键长度一致时,基于点积操作的注意力机制计算效率更高,同时还需要缩放以消除向量长度的影响。标准点积注意力(scaled dot-product attention)评分函数: $$a(q,k)=q^Tk/\sqrt{d}$$ 其中$d$表示查询和键的长度
基于PyTorch实现标准点积注意力:
#@save
class DotProductAttention(nn.Module):
"""缩放点积注意力"""
def __init__(self, dropout, **kwargs):
super(DotProductAttention, self).__init__(**kwargs)
self.dropout = nn.Dropout(dropout)
# queries的形状:(batch_size,查询的个数,d)
# keys的形状:(batch_size,“键-值”对的个数,d)
# values的形状:(batch_size,“键-值”对的个数,值的维度)
# valid_lens的形状:(batch_size,)或者(batch_size,查询的个数)
def forward(self, queries, keys, values, valid_lens=None):
d = queries.shape[-1]
# 设置transpose_b=True为了交换keys的最后两个维度
scores = torch.bmm(queries, keys.transpose(1,2)) / math.sqrt(d)
self.attention_weights = masked_softmax(scores, valid_lens)
return torch.bmm(self.dropout(self.attention_weights), values)
4 Bahdanau 注意力
在7 序列到序列学习(seq2seq)中提到了由两个RNN类网络组成的编码器-解码器架构,RNN将不定长的序列转化为定长的上下文变量,此过程容易出现信息的丢失,而引入注意力机制能极大地改善这种情况
2014年提出的Bahdanau 注意力就是一种将注意力机制引入seq2seq的经典方法,在原始版本的seq2seq中,上下文变量的计算方式很简单(直接选择最后时间步的隐状态): $$c_t=q(h_1,...,h_T)=h_T$$ 引入Bahdanau 注意力后,上下文变量的计算方式如下: $$c'_t=\Sigma_{t=1}^T\alpha(s_{t'-1},h_t)h_t$$
Bahdanau 注意力模型中,解码器隐状态$S_{t'-1}$是查询,而编码器隐状态$h_t$,既是键,也是值。函数$\alpha$可以是加性注意力打分函数。这种注意力机制的引入使得编码器的输出能更好地匹配编码器的输出,实现更有效的信息传递
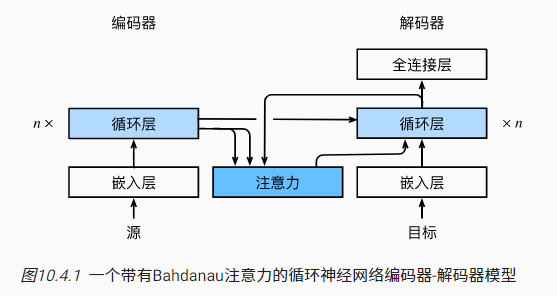
引入Bahdanau 注意力的seq2seq计算步骤:
- 原始文本通过嵌入层转化为词元的特征向量,进入编码器进行迭代
- 将编码器的全层隐状态作为解码器的初始化隐状态
- 以解码器针对上一个词的隐状态输出作为查询Q,以编码器针对每一个词的隐状态输出作为键值KV,实现Bahdanau 注意力的计算
- 拼接注意力模型的输出和下一个词的嵌入表示,作为解码器的输入
- 解码器依次输出翻译后的词元和隐状态,最后通过全连接层转换为词元的预测概率分布
基于PyTorch实现基于Bahdanau 注意力的机器翻译:
import torch
from torch import nn
from d2l import torch as d2l
#@save
class AttentionDecoder(d2l.Decoder):
"""带有注意力机制解码器的基本接口"""
def __init__(self, **kwargs):
super(AttentionDecoder, self).__init__(**kwargs)
@property
def attention_weights(self):
raise NotImplementedError
class Seq2SeqAttentionDecoder(AttentionDecoder):
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
dropout=0, **kwargs):
super(Seq2SeqAttentionDecoder, self).__init__(**kwargs)
self.attention = d2l.AdditiveAttention(
num_hiddens, num_hiddens, num_hiddens, dropout)
self.embedding = nn.Embedding(vocab_size, embed_size)
self.rnn = nn.GRU(
embed_size + num_hiddens, num_hiddens, num_layers,
dropout=dropout)
self.dense = nn.Linear(num_hiddens, vocab_size)
def init_state(self, enc_outputs, enc_valid_lens, *args):
# outputs的形状为(batch_size,num_steps,num_hiddens).
# hidden_state的形状为(num_layers,batch_size,num_hiddens)
outputs, hidden_state = enc_outputs
return (outputs.permute(1, 0, 2), hidden_state, enc_valid_lens)
def forward(self, X, state):
# enc_outputs的形状为(batch_size,num_steps,num_hiddens).
# hidden_state的形状为(num_layers,batch_size,
# num_hiddens)
enc_outputs, hidden_state, enc_valid_lens = state
# 输出X的形状为(num_steps,batch_size,embed_size)
X = self.embedding(X).permute(1, 0, 2)
outputs, self._attention_weights = [], []
for x in X:
# query的形状为(batch_size,1,num_hiddens)
query = torch.unsqueeze(hidden_state[-1], dim=1)
# context的形状为(batch_size,1,num_hiddens)
context = self.attention(
query, enc_outputs, enc_outputs, enc_valid_lens)
# 在特征维度上连结
x = torch.cat((context, torch.unsqueeze(x, dim=1)), dim=-1)
# 将x变形为(1,batch_size,embed_size+num_hiddens)
out, hidden_state = self.rnn(x.permute(1, 0, 2), hidden_state)
outputs.append(out)
self._attention_weights.append(self.attention.attention_weights)
# 全连接层变换后,outputs的形状为
# (num_steps,batch_size,vocab_size)
outputs = self.dense(torch.cat(outputs, dim=0))
return outputs.permute(1, 0, 2), [enc_outputs, hidden_state,
enc_valid_lens]
@property
def attention_weights(self):
return self._attention_weights
embed_size, num_hiddens, num_layers, dropout = 32, 32, 2, 0.1
batch_size, num_steps = 64, 10
lr, num_epochs, device = 0.005, 250, d2l.try_gpu()
# 训练
train_iter, src_vocab, tgt_vocab = d2l.load_data_nmt(batch_size, num_steps)
encoder = d2l.Seq2SeqEncoder(
len(src_vocab), embed_size, num_hiddens, num_layers, dropout)
decoder = Seq2SeqAttentionDecoder(
len(tgt_vocab), embed_size, num_hiddens, num_layers, dropout)
net = d2l.EncoderDecoder(encoder, decoder)
d2l.train_seq2seq(net, train_iter, lr, num_epochs, tgt_vocab, device)
# loss 0.021, 5827.9 tokens/sec on cuda:0
# 翻译测试并计算BLEU分数
engs = ['go .', "i lost .", 'he\'s calm .', 'i\'m home .']
fras = ['va !', 'j\'ai perdu .', 'il est calme .', 'je suis chez moi .']
for eng, fra in zip(engs, fras):
translation, dec_attention_weight_seq = d2l.predict_seq2seq(
net, eng, src_vocab, tgt_vocab, num_steps, device, True)
print(f'{eng} => {translation}, ',
f'bleu {d2l.bleu(translation, fra, k=2):.3f}')
attention_weights = torch.cat([step[0][0][0] for step in dec_attention_weight_seq], 0).reshape((
1, 1, -1, num_steps))
# 可视化注意力权重
d2l.show_heatmaps(
attention_weights[:, :, :, :len(engs[-1].split()) + 1].cpu(),
xlabel='Key positions', ylabel='Query positions')
5 多头注意力
横看成岭侧成峰,远近高低各不同;不同的视角会存在不同的注意力侧重,这一思想启迪了多头注意力(multihead attention)机制。
多头注意力(multihead attention)机制计算过程:
- 借助对相同的查询、键和值进行不同的子空间表示$(W^{(q)}q,W^{(k)}k,W^{(v)}v)$
- 并行计算每个子空间表示下的注意力,$h_i=f(W^{(q)}_iq,W^{(k)}_ik,W^{(v)}_iv)$
- 拼接$k$个不同的注意力结果,再通过全连接层进行最终的输出$W[h_1,...,h_k]^T$
多头注意力主要通过全连接层来实现查询、键和值的不同子空间表示(representation subspaces),全连接层的作用本质是一个可学习的线性变换过程
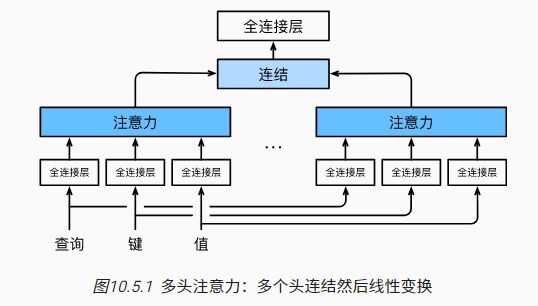
基于PyTorch实现多头注意力:
import math
import torch
from torch import nn
from d2l import torch as d2l
#@save
def transpose_qkv(X, num_heads):
"""为了多注意力头的并行计算而变换形状"""
# 输入X的形状:(batch_size,查询或者“键-值”对的个数,num_hiddens)
# 输出X的形状:(batch_size,查询或者“键-值”对的个数,num_heads,
# num_hiddens/num_heads)
X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)
# 输出X的形状:(batch_size,num_heads,查询或者“键-值”对的个数,
# num_hiddens/num_heads)
X = X.permute(0, 2, 1, 3)
# 最终输出的形状:(batch_size*num_heads,查询或者“键-值”对的个数,
# num_hiddens/num_heads)
return X.reshape(-1, X.shape[2], X.shape[3])
#@save
def transpose_output(X, num_heads):
"""逆转transpose_qkv函数的操作"""
X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])
X = X.permute(0, 2, 1, 3)
return X.reshape(X.shape[0], X.shape[1], -1)
#@save
class MultiHeadAttention(nn.Module):
"""多头注意力"""
def __init__(self, key_size, query_size, value_size, num_hiddens,
num_heads, dropout, bias=False, **kwargs):
super(MultiHeadAttention, self).__init__(**kwargs)
self.num_heads = num_heads
self.attention = d2l.DotProductAttention(dropout)
self.W_q = nn.Linear(query_size, num_hiddens, bias=bias)
self.W_k = nn.Linear(key_size, num_hiddens, bias=bias)
self.W_v = nn.Linear(value_size, num_hiddens, bias=bias)
self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias)
def forward(self, queries, keys, values, valid_lens):
# queries,keys,values的形状:
# (batch_size,查询或者“键-值”对的个数,num_hiddens)
# valid_lens 的形状:
# (batch_size,)或(batch_size,查询的个数)
# 经过变换后,输出的queries,keys,values 的形状:
# (batch_size*num_heads,查询或者“键-值”对的个数,
# num_hiddens/num_heads)
queries = transpose_qkv(self.W_q(queries), self.num_heads)
keys = transpose_qkv(self.W_k(keys), self.num_heads)
values = transpose_qkv(self.W_v(values), self.num_heads)
if valid_lens is not None:
# 在轴0,将第一项(标量或者矢量)复制num_heads次,
# 然后如此复制第二项,然后诸如此类。
valid_lens = torch.repeat_interleave(
valid_lens, repeats=self.num_heads, dim=0)
# output的形状:(batch_size*num_heads,查询的个数,
# num_hiddens/num_heads)
output = self.attention(queries, keys, values, valid_lens)
# output_concat的形状:(batch_size,查询的个数,num_hiddens)
output_concat = transpose_output(output, self.num_heads)
return self.W_o(output_concat)
6 自注意力和位置编码
6.1 自注意力与RNN、CNN的对比
对于查询和键值均来自同一组输入的注意力模型,称之为自注意力(self-attention): $$y_i=f(x_i,(x_1,x_1),...,(x_n,x_n))\in \mathbb{R}^d$$ 其中$n$表示序列长度,查询、键和值都是$n\times d$的矩阵
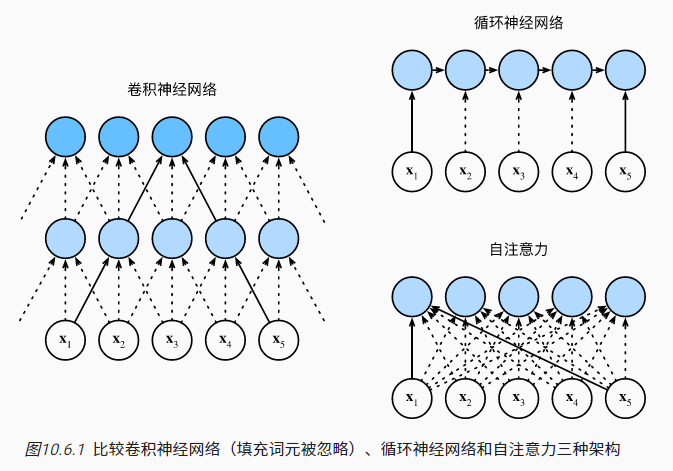
从计算复杂性、并行度和最大路径长度三个方面比RNN、CNN和self-attention:
- 顺序操作会影响并行计算,需要保证顺序的计算操作越多,并行度越低
- 计算复杂度取决于路径长度,而最大路径长度则决定了计算复杂度的上限,也决定了模型学习序列中的远距离依赖关系的难易程度(全局感知度)
- 假设滑动窗口长度为$k$,输入和输出的通道数为$d$,则卷积层的计算复杂度是$O(knd^2)$,存在$O(1)$个顺序操作,并行度为$O(n)$,最大路径长度为$O(n/k)$
- 假设隐状态维度为$d$,则RNN层的计算复杂度是$O(nd^2)$,存在$O(n)$个顺序操作,并行度为$O(1)$,最大路径长度为$O(n)$
- 假设查询、键和值都是$n\times d$的矩阵,则self-attention层的计算复杂度是$O(n^2d)$,存在$O(1)$个顺序操作,并行度为$O(n)$,最大路径长度为$O(1)$
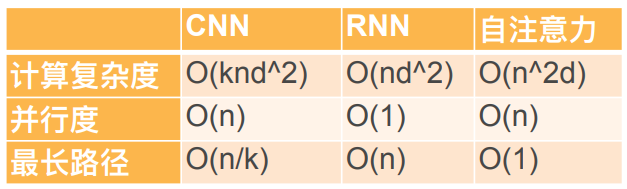
对比小结:
- 相比于CNN层,RNN层计算复杂度更低,但由于无法并行计算,实际计算效率很差
- self-attention的最大路径长度最短,具备最强的全局感知度,但是整体的计算复杂度受序列长度$n$影响较大,当序列较长时,self-attention的计算成本最高
6.2 位置编码与代码实现
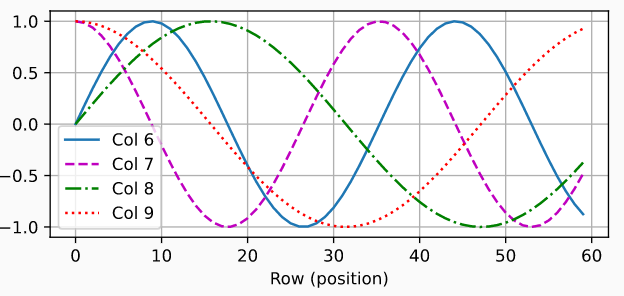
self-attention为了追求高效的并行计算而放弃了顺序操作,也丢掉了与”顺序“相关的信息,因此需要添加位置编码(positional encoding)来弥补这方面的信息损失。本小节以Sinusoidal方法为例,说明位置编码的过程
假设输入$X\in \mathbb{R}^{n\times d}$包含$n$个词元的$d$维嵌入表示,构建与$X$维度相同的位置嵌入矩阵$P$,通过$X_{input}=X+P$即可实现位置信息的添加。其中矩阵$P$中的元素需要借助正弦函数和余弦函数进行位置编码,矩阵$P$的第$i$行、第$2j$列和$2j+1$列上的元素计算过程如下: $$\begin{align} p_{i,2j}=sin(\frac{i}{10000^{2j/d}}) \\ p_{i,2j+1}=cos(\frac{i}{10000^{2j/d}}) \end{align}$$ 基于PyTorch实现位置编码:
#@save
class PositionalEncoding(nn.Module):
"""位置编码"""
def __init__(self, num_hiddens, dropout, max_len=1000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(dropout)
# 创建一个足够长的P
self.P = torch.zeros((1, max_len, num_hiddens))
X = torch.arange(max_len, dtype=torch.float32).reshape(
-1, 1) / torch.pow(10000, torch.arange(
0, num_hiddens, 2, dtype=torch.float32) / num_hiddens)
self.P[:, :, 0::2] = torch.sin(X)
self.P[:, :, 1::2] = torch.cos(X)
def forward(self, X):
X = X + self.P[:, :X.shape[1], :].to(X.device)
return self.dropout(X)
# 位置编码可视化
encoding_dim, num_steps = 32, 60
pos_encoding = PositionalEncoding(encoding_dim, 0)
pos_encoding.eval()
X = pos_encoding(torch.zeros((1, num_steps, encoding_dim)))
P = pos_encoding.P[:, :X.shape[1], :]
d2l.plot(torch.arange(num_steps), P[0, :, 6:10].T, xlabel='Row (position)',
figsize=(6, 2.5), legend=["Col %d" % d for d in torch.arange(6, 10)])
6.3 常见的位置编码-补充
绝对位置编码VS相对位置编码
- 绝对位置编码将位置信息直接融入到对应输入中,致力于对输入位置信息的完整保留
- 位置1到位置2之间的距离比位置1到位置3更近,相对位置编码会保留这类信息
- 相对位置编码的实现会更加灵活多变,NLP类模型也更依赖相对位置信息
常见的绝对位置编码方法:
- 训练式,类似于word2vec,通过参与网络训练的方式,直接把每个位置映射为一个高维向量;缺点是需要提前设定最大长度,类比word2vec的词表大小的提前确定
- 三角式,比如Sinusoidal位置编码,通过正余弦函数值域约束使得转化后的位置编码是有界且连续的(节省空间,适合参与神经网络的权重计算);不同位置的编码结果很容易进行转换(借助线性变换很容易实现的旋转+缩放),具备相对位置信息的表达
- 递归式:诸如RNN之类的递归式模型在结构上天然地具备学习位置信息的能力
- 相乘式:把位置编码结果与原始输入的加法式拼接改成乘法式拼接
相对位置编码方法相对较为灵活,相关的典型论文:
- 2018年,Goggle最早提出了相对位置编码
- Transformer-XL模型、T5模型、DeBERTa等等
其他的位置编码方法
- CNN式:padding操作对边界进行补0操作,使得模型能提取到当前位置到边界的距离
- 复数式:实现复数版本的Transformer和Embedding,构建多组词向量与位置信息结合
- 融合式:结合将绝对位置编码与相对位置编码,详情可参阅后续参考文献
本小节内容主要摘自科学空间-Transformer位置编码
7 Transformer
7.1 Transformer架构与细节
Transformer就是一种完全基于Attention的编码器-解码器架构(RNN层替换为Attention)
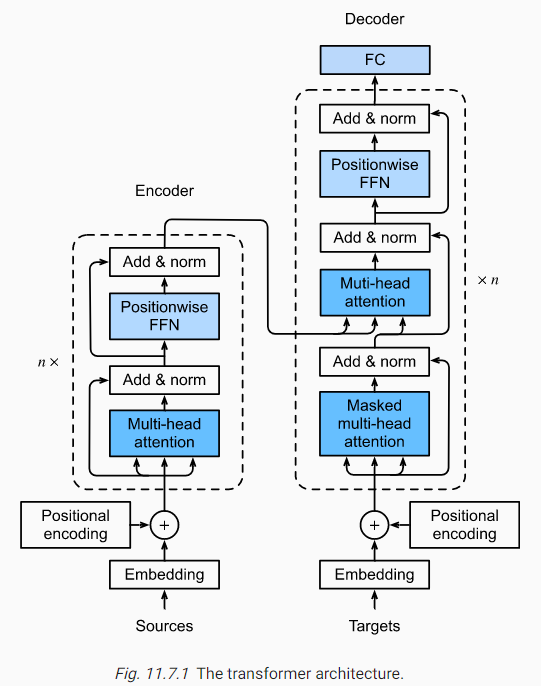
Transformer架构说明:
- 左侧为编码器(Encoder),包含$n$个编码器层(也可以看作Transform块),编码器的输入为原始序列(Sources)的嵌入表示(Embedding)和位置编码(Positional encoding)
- 右侧为解码器(Decoder),包含$n$个解码器层,输入为目标序列的嵌入表示和位置编码
- 编码器层主要包含两个部分:多头注意力(Multi-head attention,多个并列注意力层的拼接)和基于位置的前馈神经网络(Position-wise feed-forward network)
- 相比于编码器层,解码器层增加了带掩码的多头注意力(Masked multi-head attention),用于遮蔽当前位置之后的输入(模型在实际应用中不应该获取并使用来自未来的信息)
- 除此之外,在每个层中还使用了残差连接和层归一化(Add & norm)
- 解码器的输出通过全连接层转换为词元的预测概率分布
细节1:基于位置的前馈神经网络(Position-wise feed-forward network):
- 由两个全连接层组成,不同Transform块的位置前馈网络是共享的
- 假设输入维度为$(b,n,d)$,其中$b$表示batch_size,$n$表示序列长度,$d$表示特征维度
- 第一个全连接层将维度转化为$(bn,d)$,第二个全连接层将维度转化为$(b,n,d)$
- 由于网络共享,所以相同位置对应的权重计算是一致的,有助于保留位置信息?
- 位置前馈网络等价于两层窗口为1的一维卷积层
细节2:编码器与解码器之间的信息传递
- Attention中大部分多头注意力都是self-attention,即QKV是一致的
- 解码器中的多头注意力使用cross-attention,将来自编码器的输出作为KV
细节3:残差连接和层归一化(Add & norm)
- 残差连接和层规范化有利于训练层数比较深的神经网络
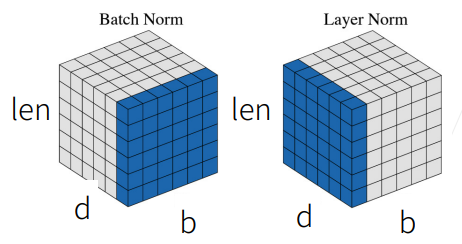
- 注意区分批量归一化(Batch Norm)和层归一化(Layer Norm)
7.2 基于PyTorch实现Transformer
import math
import pandas as pd
import torch
from torch import nn
from d2l import torch as d2l
#@save
class PositionWiseFFN(nn.Module):
"""基于位置的前馈网络"""
def __init__(self, ffn_num_input, ffn_num_hiddens, ffn_num_outputs,
**kwargs):
super(PositionWiseFFN, self).__init__(**kwargs)
self.dense1 = nn.Linear(ffn_num_input, ffn_num_hiddens)
self.relu = nn.ReLU()
self.dense2 = nn.Linear(ffn_num_hiddens, ffn_num_outputs)
def forward(self, X):
return self.dense2(self.relu(self.dense1(X)))
#@save
class AddNorm(nn.Module):
"""残差连接后进行层归一化"""
def __init__(self, normalized_shape, dropout, **kwargs):
super(AddNorm, self).__init__(**kwargs)
self.dropout = nn.Dropout(dropout)
self.ln = nn.LayerNorm(normalized_shape)
def forward(self, X, Y):
return self.ln(self.dropout(Y) + X)
#@save
class EncoderBlock(nn.Module):
"""transformer编码器块"""
def __init__(self, key_size, query_size, value_size, num_hiddens,
norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,
dropout, use_bias=False, **kwargs):
super(EncoderBlock, self).__init__(**kwargs)
self.attention = d2l.MultiHeadAttention(
key_size, query_size, value_size, num_hiddens, num_heads, dropout,
use_bias)
self.addnorm1 = AddNorm(norm_shape, dropout)
self.ffn = PositionWiseFFN(
ffn_num_input, ffn_num_hiddens, num_hiddens)
self.addnorm2 = AddNorm(norm_shape, dropout)
def forward(self, X, valid_lens): # 自注意力
Y = self.addnorm1(X, self.attention(X, X, X, valid_lens))
return self.addnorm2(Y, self.ffn(Y))
#@save
class TransformerEncoder(d2l.Encoder):
"""transformer编码器"""
def __init__(self, vocab_size, key_size, query_size, value_size,
num_hiddens, norm_shape, ffn_num_input, ffn_num_hiddens,
num_heads, num_layers, dropout, use_bias=False, **kwargs):
super(TransformerEncoder, self).__init__(**kwargs)
self.num_hiddens = num_hiddens
self.embedding = nn.Embedding(vocab_size, num_hiddens)
self.pos_encoding = d2l.PositionalEncoding(num_hiddens, dropout)
self.blks = nn.Sequential()
for i in range(num_layers):
self.blks.add_module("block"+str(i),
EncoderBlock(key_size, query_size, value_size, num_hiddens,
norm_shape, ffn_num_input, ffn_num_hiddens,
num_heads, dropout, use_bias))
def forward(self, X, valid_lens, *args):
# 因为位置编码值在-1和1之间,
# 因此嵌入值乘以嵌入维度的平方根进行缩放,
# 然后再与位置编码相加。
X = self.pos_encoding(self.embedding(X) * math.sqrt(self.num_hiddens))
self.attention_weights = [None] * len(self.blks)
for i, blk in enumerate(self.blks):
X = blk(X, valid_lens)
self.attention_weights[
i] = blk.attention.attention.attention_weights
return X
class DecoderBlock(nn.Module):
"""解码器中第i个块"""
def __init__(self, key_size, query_size, value_size, num_hiddens,
norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,
dropout, i, **kwargs):
super(DecoderBlock, self).__init__(**kwargs)
self.i = i
self.attention1 = d2l.MultiHeadAttention(
key_size, query_size, value_size, num_hiddens, num_heads, dropout)
self.addnorm1 = AddNorm(norm_shape, dropout)
self.attention2 = d2l.MultiHeadAttention(
key_size, query_size, value_size, num_hiddens, num_heads, dropout)
self.addnorm2 = AddNorm(norm_shape, dropout)
self.ffn = PositionWiseFFN(ffn_num_input, ffn_num_hiddens,
num_hiddens)
self.addnorm3 = AddNorm(norm_shape, dropout)
def forward(self, X, state):
enc_outputs, enc_valid_lens = state[0], state[1]
# 训练阶段,输出序列的所有词元都在同一时间处理,
# 因此state[2][self.i]初始化为None。
# 预测阶段,输出序列是通过词元一个接着一个解码的,
# 因此state[2][self.i]包含着直到当前时间步第i个块解码的输出表示
if state[2][self.i] is None:
key_values = X
else:
key_values = torch.cat((state[2][self.i], X), axis=1)
state[2][self.i] = key_values
if self.training:
batch_size, num_steps, _ = X.shape
# dec_valid_lens的开头:(batch_size,num_steps),
# 其中每一行是[1,2,...,num_steps]
dec_valid_lens = torch.arange(
1, num_steps + 1, device=X.device).repeat(batch_size, 1)
else:
dec_valid_lens = None
# 带掩码的多头自注意力
X2 = self.attention1(X, key_values, key_values, dec_valid_lens)
Y = self.addnorm1(X, X2)
# 编码器-解码器注意力 cross-attention
# enc_outputs的开头:(batch_size,num_steps,num_hiddens)
Y2 = self.attention2(Y, enc_outputs, enc_outputs, enc_valid_lens)
Z = self.addnorm2(Y, Y2)
return self.addnorm3(Z, self.ffn(Z)), state
class TransformerDecoder(d2l.AttentionDecoder):
"""transformer解码器"""
def __init__(self, vocab_size, key_size, query_size, value_size,
num_hiddens, norm_shape, ffn_num_input, ffn_num_hiddens,
num_heads, num_layers, dropout, **kwargs):
super(TransformerDecoder, self).__init__(**kwargs)
self.num_hiddens = num_hiddens
self.num_layers = num_layers
self.embedding = nn.Embedding(vocab_size, num_hiddens)
self.pos_encoding = d2l.PositionalEncoding(num_hiddens, dropout)
self.blks = nn.Sequential()
for i in range(num_layers):
self.blks.add_module("block"+str(i),
DecoderBlock(key_size, query_size, value_size, num_hiddens,
norm_shape, ffn_num_input, ffn_num_hiddens,
num_heads, dropout, i))
self.dense = nn.Linear(num_hiddens, vocab_size)
def init_state(self, enc_outputs, enc_valid_lens, *args):
return [enc_outputs, enc_valid_lens, [None] * self.num_layers]
def forward(self, X, state):
X = self.pos_encoding(self.embedding(X) * math.sqrt(self.num_hiddens))
self._attention_weights = [[None] * len(self.blks) for _ in range (2)]
for i, blk in enumerate(self.blks):
X, state = blk(X, state)
# 解码器自注意力权重
self._attention_weights[0][
i] = blk.attention1.attention.attention_weights
# “编码器-解码器”自注意力权重
self._attention_weights[1][
i] = blk.attention2.attention.attention_weights
return self.dense(X), state
@property
def attention_weights(self):
return self._attention_weights
# 训练
num_hiddens, num_layers, dropout, batch_size, num_steps = 32, 2, 0.1, 64, 10
lr, num_epochs, device = 0.005, 200, d2l.try_gpu()
ffn_num_input, ffn_num_hiddens, num_heads = 32, 64, 4
key_size, query_size, value_size = 32, 32, 32
norm_shape = [32]
train_iter, src_vocab, tgt_vocab = d2l.load_data_nmt(batch_size, num_steps)
encoder = TransformerEncoder(
len(src_vocab), key_size, query_size, value_size, num_hiddens,
norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,
num_layers, dropout)
decoder = TransformerDecoder(
len(tgt_vocab), key_size, query_size, value_size, num_hiddens,
norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,
num_layers, dropout)
net = d2l.EncoderDecoder(encoder, decoder)
d2l.train_seq2seq(net, train_iter, lr, num_epochs, tgt_vocab, device)
# loss 0.033, 5849.7 tokens/sec on cuda:0
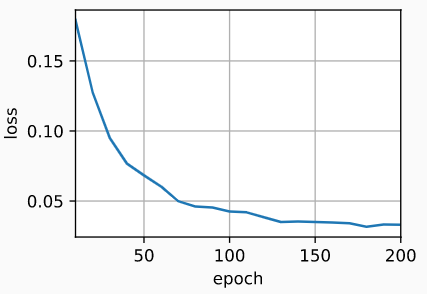
预测与注意力可视化:
# 预测与BLEU分数计算
engs = ['go .', "i lost .", 'he\'s calm .', 'i\'m home .']
fras = ['va !', 'j\'ai perdu .', 'il est calme .', 'je suis chez moi .']
for eng, fra in zip(engs, fras):
translation, dec_attention_weight_seq = d2l.predict_seq2seq(
net, eng, src_vocab, tgt_vocab, num_steps, device, True)
print(f'{eng} => {translation}, ',
f'bleu {d2l.bleu(translation, fra, k=2):.3f}')
# go . => va !, bleu 1.000
# i lost . => je vous en prie ., bleu 0.000
# he's calm . => il est calme ., bleu 1.000
# i'm home . => je suis chez moi ., bleu 1.000
# 编码器多头自注意力可视化
enc_attention_weights = torch.cat(net.encoder.attention_weights, 0).reshape((num_layers, num_heads,
-1, num_steps))
d2l.show_heatmaps(
enc_attention_weights.cpu(), xlabel='Key positions',
ylabel='Query positions', titles=['Head %d' % i for i in range(1, 5)],
figsize=(7, 3.5))
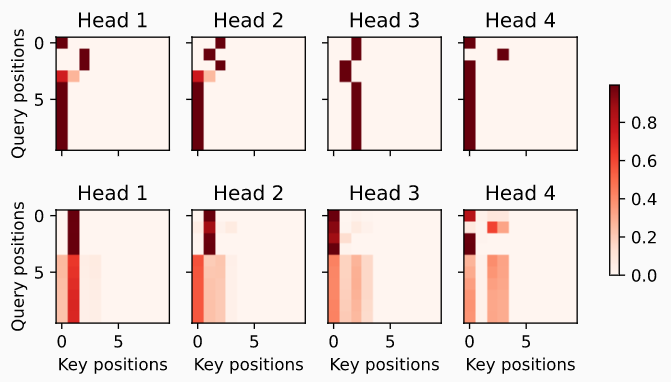
# 数据预处理
dec_attention_weights_2d = [head[0].tolist()
for step in dec_attention_weight_seq
for attn in step for blk in attn for head in blk]
dec_attention_weights_filled = torch.tensor(
pd.DataFrame(dec_attention_weights_2d).fillna(0.0).values)
dec_attention_weights = dec_attention_weights_filled.reshape((-1, 2, num_layers, num_heads, num_steps))
dec_self_attention_weights, dec_inter_attention_weights = \
dec_attention_weights.permute(1, 2, 3, 0, 4)
dec_self_attention_weights.shape, dec_inter_attention_weights.shape
# Plusonetoincludethebeginning-of-sequencetoken
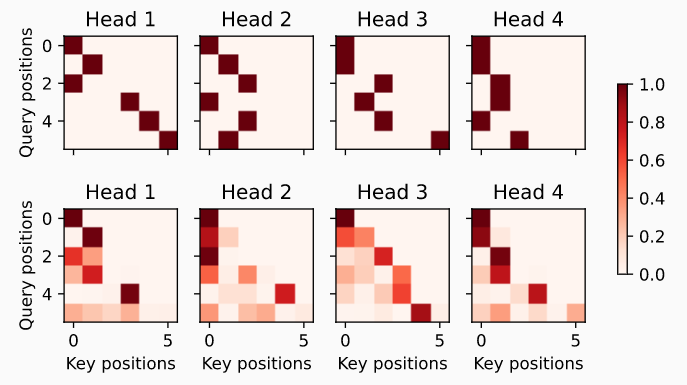
# 解码器多头self-attention可视化
d2l.show_heatmaps(
dec_self_attention_weights[:, :, :, :len(translation.split()) + 1],
xlabel='Key positions', ylabel='Query positions',
titles=['Head %d' % i for i in range(1, 5)], figsize=(7, 3.5))
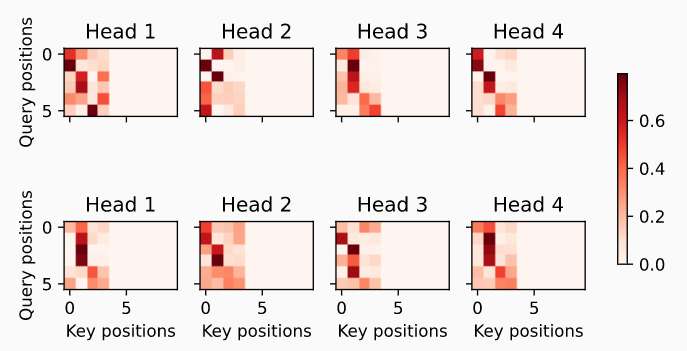
# 解码器多头cross-attention可视化
d2l.show_heatmaps(
dec_inter_attention_weights, xlabel='Key positions',
ylabel='Query positions', titles=['Head %d' % i for i in range(1, 5)],
figsize=(7, 3.5))
8 Transformer的图像应用
用Transformer结构替换CNN层从理论上是可行的,这也意味着Transformer或许也可以在图像领域大展拳脚。而伴随着对Transformer的能力挖掘,ViTs(vision transformers)类模型具备极强的可拓展性,并在“大数据大模型”等场景下展现出显著优势
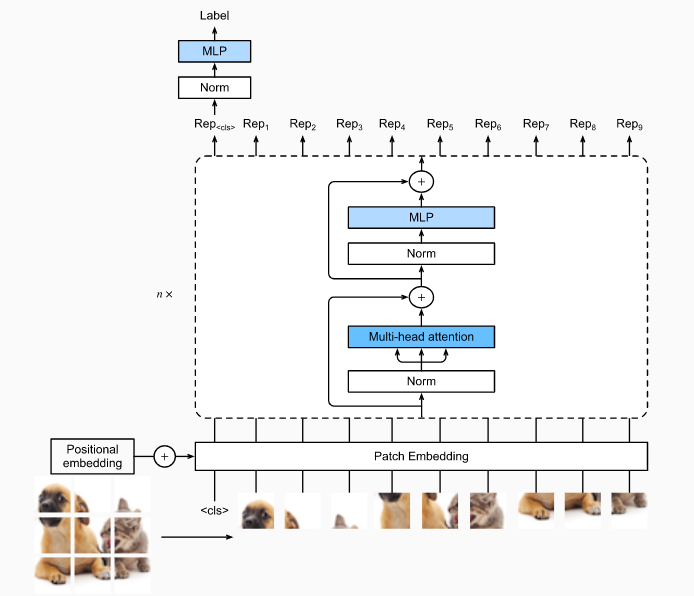
一种Transformer应用于图像的常见思路:
- 切分图像,转化为一系列的patches构成的序列(模拟文本序列的输入形式);起始点为特殊占位符
<cls>,用于方便后续的的预测标签输出 - 对每个patch进行嵌入表示(PatchEmbedding),并添加位置编码(PositionalEmbedding)
- 并联$n$个(预归一化Norm,多头注意力Mutil-head attention,层归一化Norm,多层感知机MLP),其中每个MLP都添加Dropout进行正则化,并将激活函数从ReLU替换为GELU
- 将占位符
<cls>对应的编码器输出作为输入的全局表示,通过Norm+MLP实现最终的预测
预归一化:pre-normalization,在MLP之前进行归一化,相比于普通归一化(残差链接后再进行层归一化),预归一化有助于Transformer更高效地训练
GELU:Gaussian Error Linear Unit 高斯误差线性单元,可看作一种平滑版本的ReLu
基于PyTorch实现图像应用的代码demo
import torch
from torch import nn
from d2l import torch as d2l
# 构建子图的嵌入表示
class PatchEmbedding(nn.Module):
def __init__(self, img_size=96, patch_size=16, num_hiddens=512):
super().__init__()
def _make_tuple(x):
if not isinstance(x, (list, tuple)):
return (x, x)
return x
img_size, patch_size = _make_tuple(img_size), _make_tuple(patch_size)
self.num_patches = (img_size[0] // patch_size[0]) * (
img_size[1] // patch_size[1])
self.conv = nn.LazyConv2d(num_hiddens, kernel_size=patch_size,
stride=patch_size)
def forward(self, X):
# Output shape: (batch size, no. of patches, no. of channels)
return self.conv(X).flatten(2).transpose(1, 2)
# MLP使用dropout进行正则化,使用GELU作为激活函数
class ViTMLP(nn.Module):
def __init__(self, mlp_num_hiddens, mlp_num_outputs, dropout=0.5):
super().__init__()
self.dense1 = nn.LazyLinear(mlp_num_hiddens)
self.gelu = nn.GELU()
self.dropout1 = nn.Dropout(dropout)
self.dense2 = nn.LazyLinear(mlp_num_outputs)
self.dropout2 = nn.Dropout(dropout)
def forward(self, x):
return self.dropout2(self.dense2(self.dropout1(self.gelu(
self.dense1(x)))))
# 多头注意力和MLP构成ViT块
class ViTBlock(nn.Module):
def __init__(self, num_hiddens, norm_shape, mlp_num_hiddens,
num_heads, dropout, use_bias=False):
super().__init__()
self.ln1 = nn.LayerNorm(norm_shape)
self.attention = d2l.MultiHeadAttention(num_hiddens, num_heads,
dropout, use_bias)
self.ln2 = nn.LayerNorm(norm_shape)
self.mlp = ViTMLP(mlp_num_hiddens, num_hiddens, dropout)
def forward(self, X, valid_lens=None):
X = self.ln1(X)
return X + self.mlp(self.ln2(
X + self.attention(X, X, X, valid_lens)))
# ViTs模型整体结构
class ViT(d2l.Classifier):
"""Vision transformer."""
def __init__(self, img_size, patch_size, num_hiddens, mlp_num_hiddens,
num_heads, num_blks, emb_dropout, blk_dropout, lr=0.1,
use_bias=False, num_classes=10):
super().__init__()
self.save_hyperparameters()
self.patch_embedding = PatchEmbedding(
img_size, patch_size, num_hiddens)
self.cls_token = nn.Parameter(torch.zeros(1, 1, num_hiddens))
num_steps = self.patch_embedding.num_patches + 1 # Add the cls token
# Positional embeddings are learnable
self.pos_embedding = nn.Parameter(
torch.randn(1, num_steps, num_hiddens))
self.dropout = nn.Dropout(emb_dropout)
self.blks = nn.Sequential()
for i in range(num_blks):
self.blks.add_module(f"{i}", ViTBlock(
num_hiddens, num_hiddens, mlp_num_hiddens,
num_heads, blk_dropout, use_bias))
self.head = nn.Sequential(nn.LayerNorm(num_hiddens),
nn.Linear(num_hiddens, num_classes))
def forward(self, X):
X = self.patch_embedding(X)
X = torch.cat((self.cls_token.expand(X.shape[0], -1, -1), X), 1)
X = self.dropout(X + self.pos_embedding)
for blk in self.blks:
X = blk(X)
return self.head(X[:, 0])
# 模型训练
img_size, patch_size = 96, 16
num_hiddens, mlp_num_hiddens, num_heads, num_blks = 512, 2048, 8, 2
emb_dropout, blk_dropout, lr = 0.1, 0.1, 0.1
model = ViT(img_size, patch_size, num_hiddens, mlp_num_hiddens, num_heads,
num_blks, emb_dropout, blk_dropout, lr)
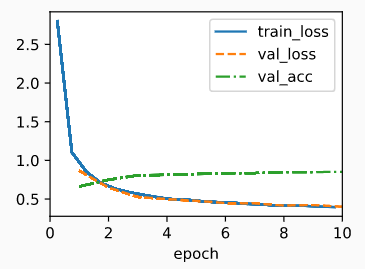
trainer = d2l.Trainer(max_epochs=10, num_gpus=1)
data = d2l.FashionMNIST(batch_size=128, resize=(img_size, img_size))
trainer.fit(model, data)
9 针对Transformers的大规模预训练
通过大规模数据针对模型进行预训练,能极大地增强模型的泛化能力
Transformers主要包含三种模式:纯编码器、编码器-解码器和纯解码器
9.1 纯编码器 Encoder-Only
纯编码器示例:BERT(Bidirectional Encoder Representations from Transformers)
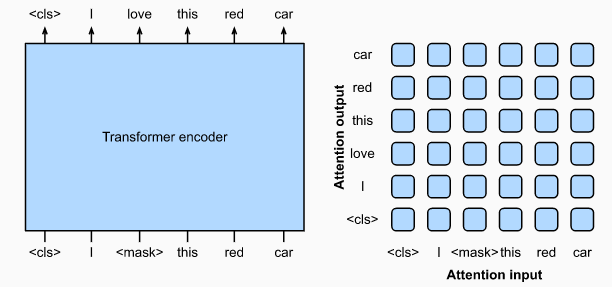
BERT(2018)是一种遮掩语言模型(masked language modeling)
- BERT输入是经过随机遮掩后的词元,模型目标是预测这些被遮掩的词元
- BERT会利用上下文进行词元的预测,因此是一种双向编码器(Bidirectional Encoder)
- BERT不需要数据标注,因此可以利用大规模文本进行预训练,原始BERT训练数据集达到了2500亿,模型可训练参数约3.5亿,因此BERT实现了很高的模型泛化能力
- BERT可以通过微调(fine-tuned)应用于很多下游任务,包括但不限于文本分类、文本标记、问题回答等任务,并取得了当时的最优效果(state of the art)
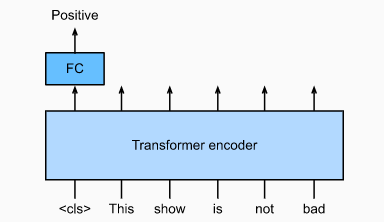
BERT的微调示例:
- 以情感分析为例,将BERT中特殊占位符
<CLS>对应输出外接全连接层 - 基于情感分析的带标注数据进行训练,目标函数是预测分类与实际分类的交叉熵
- 训练主要是调整新增的全连接层参数,也可以针对BERT原始参数进行再训练
围绕BERT,后续提出了很多变种模型和改进方法,包括但不限于ReBERTa(修正训练任务、增大数据和参数量)、ALBERT(嵌入矩阵分解、强制参数共享)、SpanBERT(遮蔽连续的词元)、DistilBERT(引入知识蒸馏,模型轻量化)、ELECTRA(增加了判断词元是否替换的判别器)等等
9.2 编码器-解码器 Encoder-Decoder
最初的Transformer架构就是应用于机器翻译的Encoder-Decoder结构;相比于Encoder-Only结构,Encoder-Decoder需要借助交叉注意力(cross-attention)汇总Encoder和Decoder的输出信息,同时还要注意Decoder存在序列方向约束(只能使用当前或之前的信息,不能使用来自未来的信息)
BART(2019) 和 T5(2020)是最早的两个基于大规模文本预料训练的Encoder-Decoder结构Transformer模型,其中前者强调对于噪声的引入(掩码、删减、旋转),后者注重多任务的协同和全面的消融实验。本小节后续将以T5为例进行简略说明
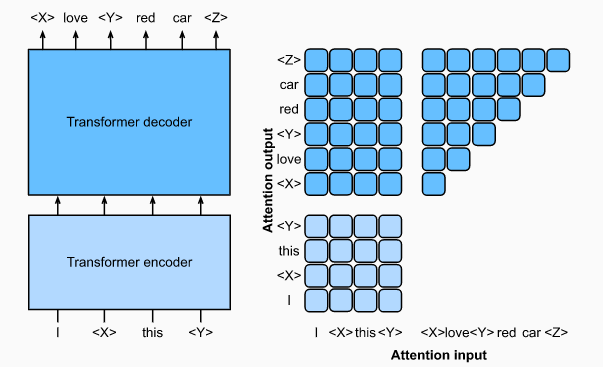
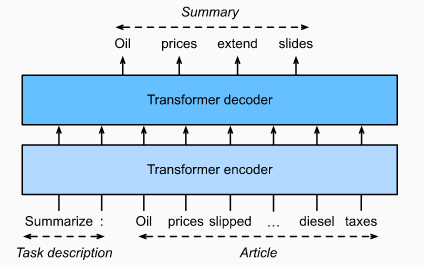
T5是一种文本输入、文本输出的Transformer结构模型
- T5模型的输入包括任务描述和文本输入,假设任务描述为"行业类型",文本输入为”这座工厂每年产出10W吨罐头“,则模型输出可能就是”这座工厂的行业类型是食品类“
- T5的预训练过程是重建受损的文本序列(与BERT的词遮蔽是类似的),以”I love red car“为例,利用特殊占位符随机遮蔽其中的连续词元,模型的编码器输入为”I
<X>red<Y>“,模型的解码器输出目标则是”<X>love<Y>red car<Z>“ - T5包含110亿参数,在文本分类和生成等领域取得了出色的效果。模型预训练使用的英文语料来自网络,经过清洗后包含约1W亿词元
T5的微调:
- 相比于BERT的微调,T5不需要增加额外的层,只需要输入相应的任务描述
- T5由于包含transformer decoder,所以输出文本长度可以是不固定的
9.3 纯解码器 Decoder-Only
目前的大规模语言模型的主流架构就是 Decoder-Only Transformer
Decoder-Only中的典型便是GPT系列模型:GPT、GPT2、GPT3
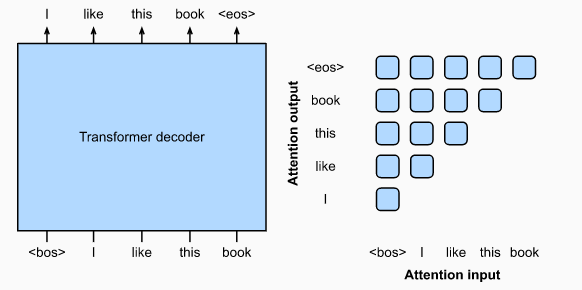
GPT是一种生成式预训练模型:
- GPT的输入是一条文本序列,输出目标是平移后的输入文本序列
- GPT使用特殊占位符
<bos>和<eos>标记序列的首尾位置 - 2018年推出的GPT模型包含1亿个参数,对于下游任务需要微调
- 2019年推出的GPT2模型采用了预归一化、权重缩放等技巧,基于40G文本语料进行预训练,最终模型参数量达到了15亿,即使不进行微调,在很多下游任务也有着出色的表现
- 2020年推出的GPT3模型架构和GPT2相似,但是语料和模型参数量又提高了两个数量级,实现了更优质的表现,但相比于针对特定任务微调后的模型还是会略有不足
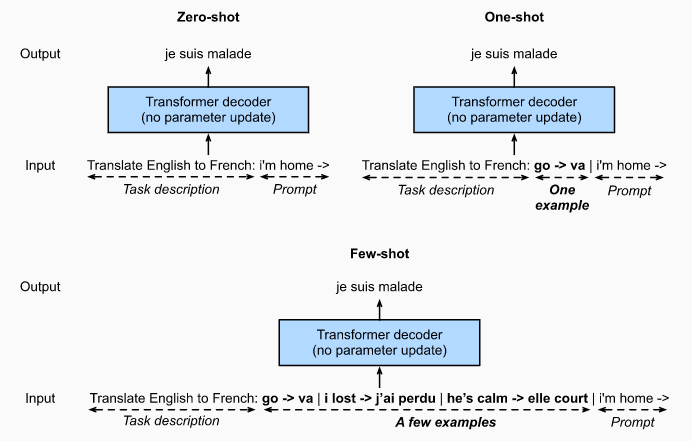
围绕海量数据训练得到的 Decoder-Only模型,在应用到下游任务时已经不再需要进行模型参数的更新,而是存在另外三种常用的学习范式:
- zero-shot:提供任务描述,不提供样本示例
- one-shot:提供任务描述,提供单条样本示例
- few-shot:提供任务描述,提供少量样本示例
9.4 可拓展性与总结
研究表明:
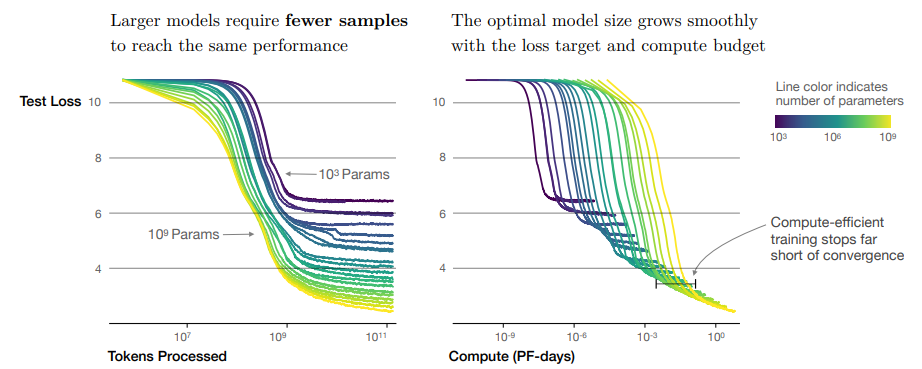
- 模型表现与计算量、数据规模、模型复杂度之间存在幂律关系
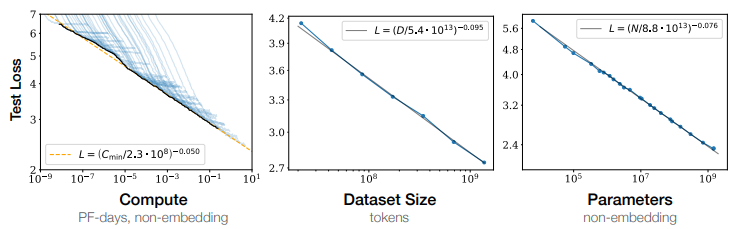
- 相比复杂度较低的模型,高复杂度模型只需要更少的样本就能达到同样的性能表现
除了NLP,Transformer架构在其他领域也有着出色的表现:
- Chinchilla 在Flamingo的基础上进行拓展,实现了基于少样本的视觉语言模型
- DALL-E 2文本转图像系统融合了来自GPT-2、GLIP的文本和图像嵌入表示
- Parti展现出了基于Transformer的多模态预训练在文本转图像方面的巨大潜能