1 知识图基本介绍
知识图(Knowledge graph):以图的形式存储知识
- 节点表示实体(entitles),节点的标签可以是实体类型
- 节点之间的边表示两个实体之间的关系
- 所以知识图是异构图的一种特殊情况
知识图示例:生物知识图(蛋白质/药物/疾病/不良事件)
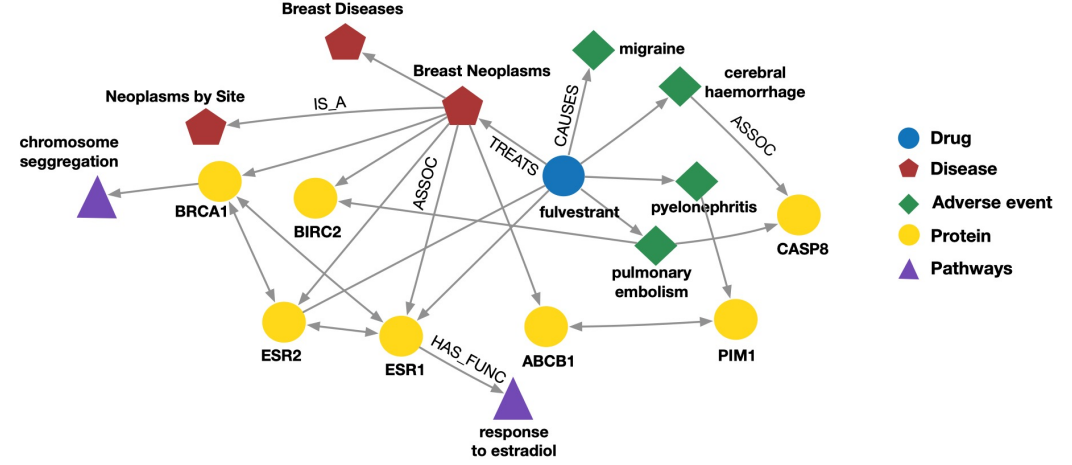
知识图应用:信息检索服务、问答和对话
常见的开源 KG :知识图数据资源
这类知识图一般是百万级别的,存在很多边的缺失(考虑补齐)
比如 Freebase 中 93.8%的人没有出生地、78.5%的人没有国籍
2 知识图嵌入表示
定义知识图中的三元组:(h,r,t)->(头,关系,尾)
知识图嵌入表示的主要思想:
- 先将实体和实体间的关系转化到 $d$ 维的嵌入空间
- $(h,r)$ 的嵌入表示应该尽可能接近 $t$ 的嵌入表示
- 定义相似性得分 $f_r(h,t)$ 来表示三元组
(h,r,t)存在的可能性
知识图嵌入表示的核心是知识补齐:能根据 $(h,r)$ 预测 $t$
主流的知识图嵌入表示方法:
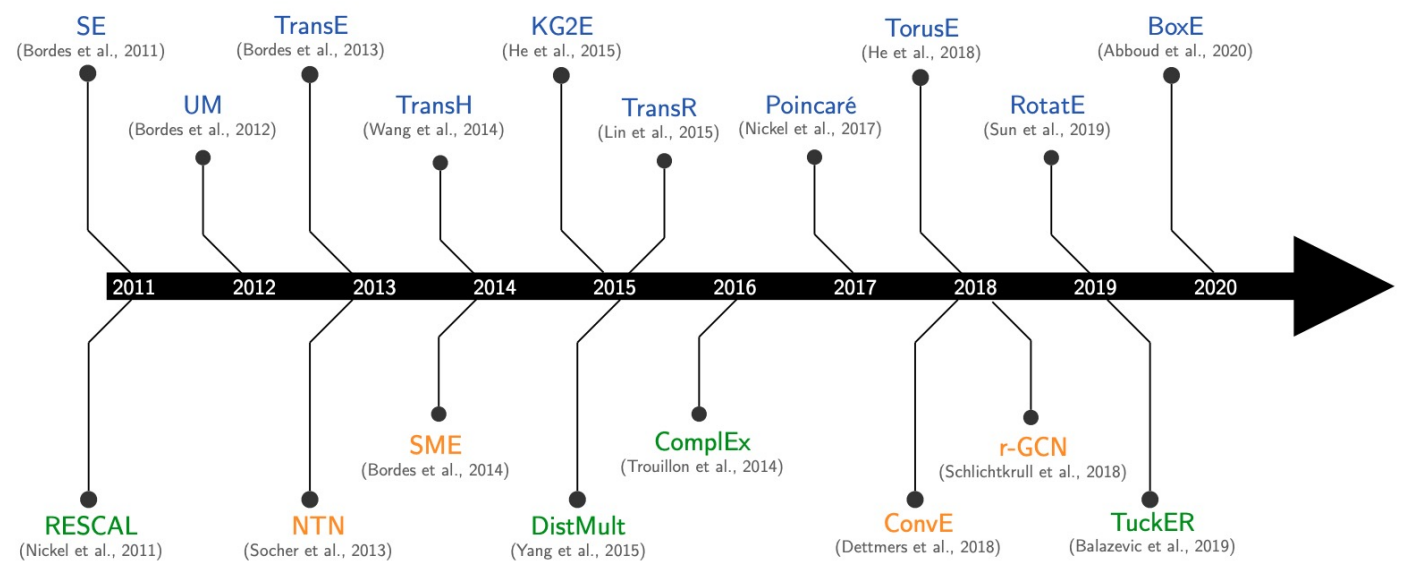
不同方法间的区别主要在于:(1)不同的几何直觉(2)不同的表达能力/关系类型
本节课主要涉及以下四种常见的知识图嵌入表示方法:
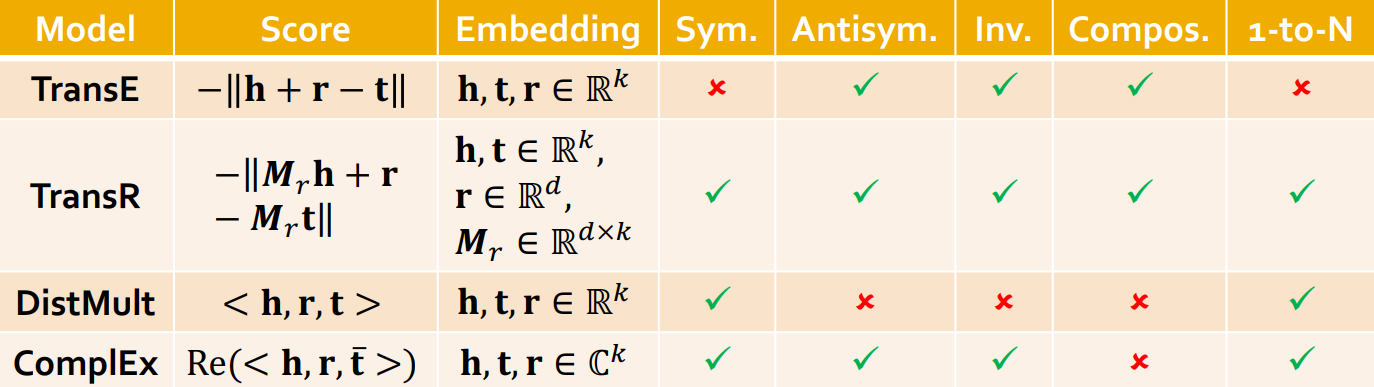
- Score(相似度得分):欧式距离度量(前两个),余弦相似度(后两个)
- Sym(对称性):A 是 B 的朋友 -> B 也是 A 的朋友
- Antisym(反对称性):A 是 B 的父亲 -> B 不是 A 的父亲
- Inv(逆关系):A 是 B 的父亲 -> B 是 A 的孩子
- Compos(复合关系):B 是女的,A 是 B 的父亲 -> B 是 A 的女儿
- 1-to-N(一对多关系):A 是 B 的父亲 -> A 也可以是 C 的父亲
经验总结:(1)不同 KG 的关系模型差异很大,不存在适用于所有 KG 的统一嵌入方法,需要因图制宜(2)当 KG 中不存在太多对称关系时,可考虑先用 TransE 快速实现;然后再使用其他更具表现力的模型,比如 CompIEx、RotatE(复数空间版的 TransE)
3 知识图嵌入表示:TransE
TransE 的算法步骤:

- 基于均匀分布初始化实体 $e$ 和实体关系 $r$,其中 $k$ 表示嵌入表示维度
- 每次迭代时,从训练集 $S$ 中随机筛选 $b$ 个三元组 $(h,r,t)$,并分布构建对应的负样本 $(h',r,t')$ ,即在实际的 KG 中不存在的三元组;然后将正负样本纳入一个训练批次的集合 $T_{batch}$ 中
- TransE 算法使用对比损失函数指导参数的更新;该损失函数的目的是尽可能提高正样本的得分并降低负样本的得分;其中得分函数为三元组的距离评估函数:$-||h+r-t||$
TransE 的算法分析:
- TransE 可以建模反对称性:$h+r=t,but\ t+r\neq h$
- TransE 可以建模逆关系:$(h,r_2,t)->(t,r_1,h),when \ r_1=-r_2$
- TransE 可以建模复合关系:$r_1(x,y)\land r_2(y,z)\Rightarrow r_3(x,z) ,when \ r_3= r_1+r_2$
- TransE 不支持建模对称性和一对多关系
4 知识图嵌入表示:TransR
TransR 算法在 TransE 基础上的改进:
- 为实体关系构建单独的嵌入表示空间,并与实体区分
- 更新评分函数为:$-||M_rh+r-M_rt||$
实体 $e$ 和关系 $r$ 处于不同的嵌入表示空间,所以需要额外的线性投影 $M_r$
TransR 的算法分析:
- TransR 算法继承了 TransE 算法的所有建模能力
- TransR 可以建模对称性:不同的关系 $r$ 有不同的投影 $M_r$
- TransR 可以建模一对多关系:通过 $M_r$ 学习实现 $M_rt_1=M_rt_2$
5 知识图嵌入表示:DistMult
DistMult 算法在 TransE 基础上的改进:
- 用矩阵 $A$ 来包含关系信息,追求 $hA$ 尽可能接近 $t$
- 评分函数不再使用 L1/L2 距离,而是改用余弦相似度
- 限制矩阵 A 为对角矩阵,抑制矩阵 A 的表达(避免过拟合)
- 因此 DistMult 的得分函数为:$h\cdot A \cdot t=\Sigma_i(h_i\cdot r_i \cdot t_i)=<h,r,t>$
DistMult 的算法分析:
- 因为点积是可交换的,所以 DistMult 不区分头实体和尾实体
- DistMult 算法可以建模对称性:$<h,r,t>=<t,r,h>$
- DistMult 算法可以建模一对多关系:$<h,r,t_1>=<h,r,t_2>$
- DistMult 算法不可以建模反对称性、逆关系、复合关系
6 知识图嵌入表示:CompIEx
CompIEx 算法在 DistMult 基础上的改进:
- 将实体和关系共同嵌入表示在一个复数向量空间
- CompIEx 算法的评分函数为:$\mathrm{Re}\left (\sum_i\mathbf{h}_i\cdot\mathbf{r}_i\cdot\bar{\mathbf{t}}_i\right)$
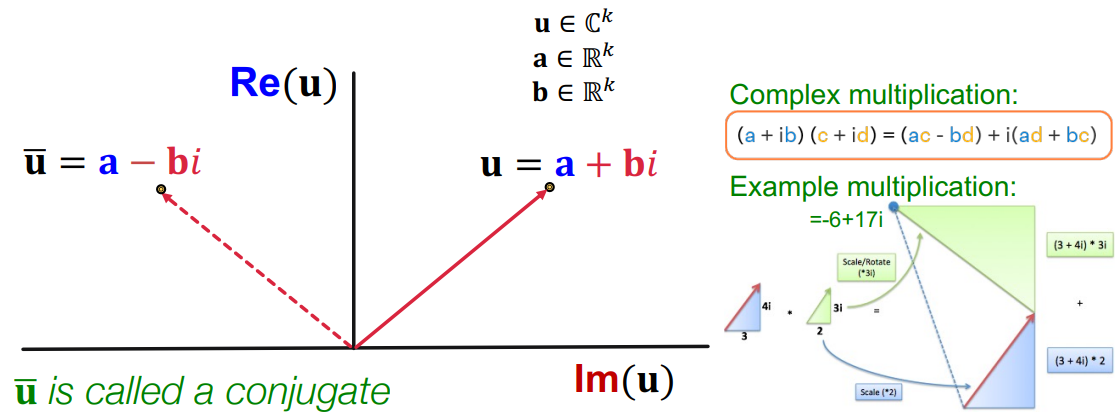
$\mathrm{Re}(u)$ 表示 $u$ 的实部;$\mathrm{Im}(u)$ 表示 $u$ 的虚部;$\bar{\mathbf{u}}$ 表示 $\mathbf{u}$ 的共轭
CompIEx 评分函数的化简: $$\begin{aligned} f_r(h,t)&=\mathrm{Re}\left(\sum_i\mathbf{h}_i\cdot\mathbf{r}_i\cdot\bar{\mathbf{t}}_i\right) =\sum_i\mathrm{Re}(\mathbf{h}_i\cdot\mathbf{r}_i\cdot\overline{\mathbf{t}}_i) \\ &=\sum_i\mathrm{Re}((\mathrm{Re}(\mathbf{h}_i)+i\mathrm{Im}(\mathbf{h}_i))\cdot(\mathrm{Re}(\mathbf{r}_i)+i\mathrm{Im}(\mathbf{r}_i))\cdot(\mathrm{Re}(\mathbf{t}_i)-i\mathrm{Im}(\mathbf{t}_i))) \\ &=\sum_i[\mathrm{Re}(\mathbf{h}_i)\mathrm{Re}(\mathbf{r}_i)\mathrm{Re}(\mathbf{t}_i)+ \mathrm{Re}(\mathbf{h}_i)\mathrm{Im}(\mathbf{r}_i)\mathrm{Im}(\mathbf{t}_i)+ \mathrm{Im}(\mathbf{h}_i)\mathrm{Re}(\mathbf{r}_i)\mathrm{Im}(\mathbf{t}_i)+ \mathrm{Im}(\mathbf{h}_i)\mathrm{Im}(\mathbf{r}_i)\mathrm{Re}(\mathbf{t}_i)] \\ &=\langle\mathrm{Re}(\mathbf{h}_i),\mathrm{Re}(\mathbf{r}_i),\mathrm{Re}(\mathbf{t}_i)\rangle+ \langle\mathrm{Im}(\mathbf{h}_i),\mathrm{Re}(\mathbf{r}_i),\mathrm{Im}(\mathbf{t}_i)\rangle+ \langle\mathrm{Im}(\mathbf{h}_i),\mathrm{Im}(\mathbf{r}_i),\mathrm{Re}(\mathbf{t}_i)\rangle- \langle\mathrm{Im}(\mathbf{h}_i),\mathrm{Im}(\mathbf{r}_i),\mathrm{Re}(\mathbf{t}_i)\rangle \end{aligned}$$
CompIEx 的算法分析:
- 通过复共轭的不对称建模, CompIEx 可以建模反对称性
- CompIEx 可以建模对称性:$f_r(h,t)=\mathrm{Re}\left (\sum_i\mathbf{h}_i\cdot\mathbf{r}_i\cdot\bar{\mathbf{t}}_i\right)=\mathrm{Re}\left (\sum_i\mathbf{r}_i\cdot\bar{\mathbf{h}}_i\cdot\mathbf{t}_i\right)=f_r(t,h)$
- CompIEx 可以建模逆关系:$r_2(h,t)\rightarrow r_1(t,h)\ when \ r_1 = \bar{r_2}$
- CompIEx 可以建模一对多关系,不可以建模复合关系(和 DistMult 算法一致)