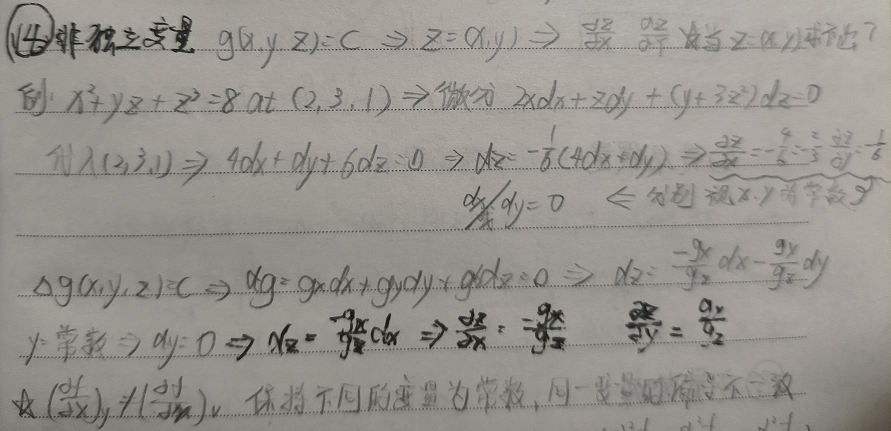1 非独立变量的依赖
当给定函数$g(x,y,z)=c$的形式时,一般可以转化为$z=z(x,y)$的形式,然后进行推导出变量$z$与变量$x,y$之间的偏导(依赖关系),即: $$\frac{\partial{z}}{\partial{x}},\frac{\partial{z}}{\partial{y}}$$ 问题:当$z=z(x,y)$的形式无法求解时,如何求解变量$z$与变量$x,y$之间的偏导?
例题:$x^2+yz+z^3=8$,求$z(x,y)$在点$(2,3,1)$处的偏导值
对原函数求微分可得:$2xdx+zdy+(y+3z^2)dz=0$ 带入$(x,y,z)=(2,3,1)$可得:$4dx+dy+6dz=0$,所以$dz=-\frac{1}{6}(4dx+dy)$ 固定$x$(视$x$为常数),此时$dx=0$,可得$\frac{\partial{z}}{\partial{y}}=-\frac{1}{6}$,同理可得$\frac{\partial{z}}{\partial{x}}=-\frac{2}{3}$
2 非独立变量偏导的一般形式
当函数$g(x,y,z)=c$时,微分可得$dg=g_xdx+g_ydy+g_zdz=0$
化简得到$dz$的一般形式:
$$dz=-\frac{g_x}{g_z}dx-\frac{g_y}{g_z}dy$$ 3. 固定变量$y$,使得$dy=0$,可得变量$z$与变量$x$的依赖关系: $$\frac{\partial{z}}{\partial{x}}=\frac{-g_x}{g_z}$$ 4. 固定变量$x$,使得$dx=0$,可得变量$z$与变量$y$的依赖关系: $$\frac{\partial{z}}{\partial{y}}=\frac{-g_y}{g_z}$$
以上过程其实是链式法则的另一种形式,二者本质上是一致的
3 符号的使用规范
保持不同的变量为常数,同一个变量的偏导是不一致的
示例:$f(x,y)=x+y$,假设$x=u,y=u+v$,则$f(u,v)=2u+v$。分别计算偏导$\frac{\partial{f}}{\partial{x}}=1$,$\frac{\partial{f}}{\partial{u}}=2$,这与$x=u$的前提假设相悖
分析:出现悖论的原因在于未明确计算偏导的过程中哪些变量是固定不变的
为了方便起见,用$(\frac{\partial{f}}{\partial{x}})_y$表示变量$y$固定时,变量$x$对函数$f$的偏导 而当计算变量$u$对函数$f$的偏导,固定的变量是$v$,即$(\frac{\partial{f}}{\partial{u}})_v$,所以实际情况如下: $$(\frac{\partial{f}}{\partial{u}})_v=(\frac{\partial{f}}{\partial{x}})_v\neq(\frac{\partial{f}}{\partial{x}})_y$$
4 参考