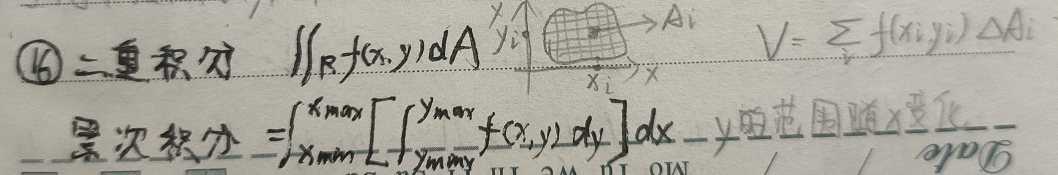1 二重积分
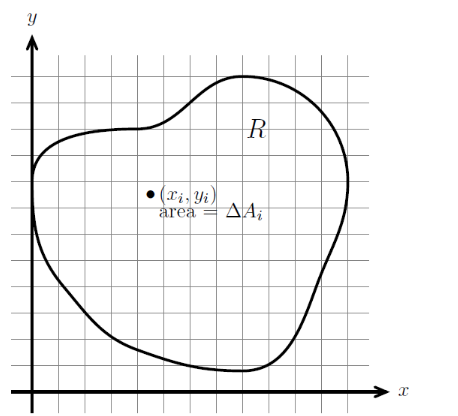
假设存在区域$R$与函数$f(x,y)$,对区域$r$进行网格化分割,其中第$i$块小格的面积为$\Delta A_i$,并且该小格的中心坐标为$(x_i,y_i)$,则函数$f$在区域$R$内的二重积分可表示如下: $$\int \! \! \!\int_{R} f(x,y)dA=\int \! \! \!\int_{R} f(x,y)dA$$ 其中,$dA$可以看作$dx$与$dy$的乘积(小格子都被近似看作为矩阵)
考虑单变量积分,其积分值表示函数曲线在特定区间下围绕产生的面积值。
同理,二重积分的几何含义是函数曲面在特定区域下围绕产生的体积值:$$V=\Sigma_i f(x_i,y_i)\Delta A_i$$
2 二重积分计算
对于二重积分,需要转化为累次积分进行多次积分的计算: $$\int_{x_{min}}^{x_{max}}[\int_{y_{min}}^{y_{max}}f(x,y)dy]dx$$ 例题:计算函数$z=1-x^2-y^2$在区间$0\leq x\leq 1$,$0\leq y\leq 1$上的积分
分析:先固定一个变量进行内部的积分,再进行外部的积分
- 固定$x$为常数,进行内部积分:$\int_0^1(1-x^2-y^2)dy=[(1-x^2)y-\frac{1}{3}y^3]_0^1=\frac{2}{3}-x^2$
- 外部积分,得到积分结果:$\int_0^1(\frac{2}{3})dx=[\frac{2}{3}-\frac{1}{3}x^3]_0^1=\frac{1}{3}$
3 交换积分顺序
有时交换积分顺序后,积分会更容易计算。但要注意外部积分的上下限是依赖于内部积分的上下限的,因此交换积分顺序后需要注意上下限的可能变动
例题:计算$\int_0^1 \int_x^{\sqrt(x)}\frac{e^y}{y}dydx$
分析:直接积分无法求解,考虑交换积分次序
- 交换积分次序,注意转换上下限:$\int_0^1 \int_{y^2}^y\frac{e^y}{y}dxdy$
- 固定$y$为常数,进行内部积分:$\int_0^1 e^y-ye^ydy$
- 外部积分,得到积分结果:$[-ye^y+2e^y]_0^1=e-2$
4 参考