1 AC 算法概况
AC 算法，即 Aho-Corasick 自动机算法，是两位创始人的名称凑出来的（国际惯例起名法了属于是，但是简称和强化学习里的 Actor-Critic 算法重名，需要注意区分~）
此算法的时间复杂度为O(n)，与匹配字符串的数目无关，只跟被匹配字符串长度有关
特性：核心思想和单模式匹配算法KMP（建议先看懂这个）是一致的，都通过寻找字符串的内部规律，达到每次失配时的高效跳转，只不过AC算使用前缀树来存放所有模式串的前缀，然后通过失配指针来处理失配的情况。
2 构建前缀字典树（生成goto表）
举例：以字符串 i, he, his, she, hers, 构建字典树Trie
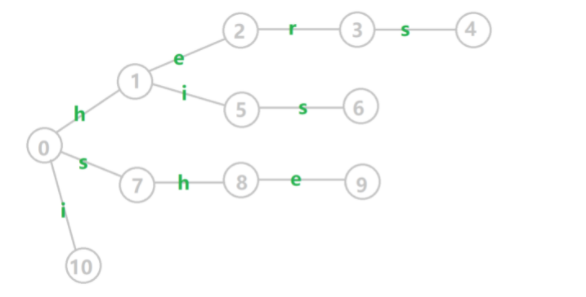
- Trie是由若干个模式串$s_1,s_2,..,s_n$构成的
- 一个结点表示一个状态，比如状态3表示
her、状态4表示hers - Trie 的边就是状态的转移，可以简单理解为加字母的过程
- 最终Trie的所有状态的集合记作$Q$，也包含了所有的子字符串可能
3 添加失配指针（生成fail表）
状态$u$的失配指针指向另一个状态$v$，其中$v\in Q$ ，且$v$是$u$的最长后缀
AC 自动机的失配指针 VS KMP 算法的 $next$ 指针
- 相同点：都在失配时用于跳转
- 不同点：$next$指针是寻找前缀后缀交集中的最长元素；而失配指针则是寻找另一个状态，另一个状态的后缀需要与当前状态的后缀重合度最高
添加失配指针的整体流程如下：
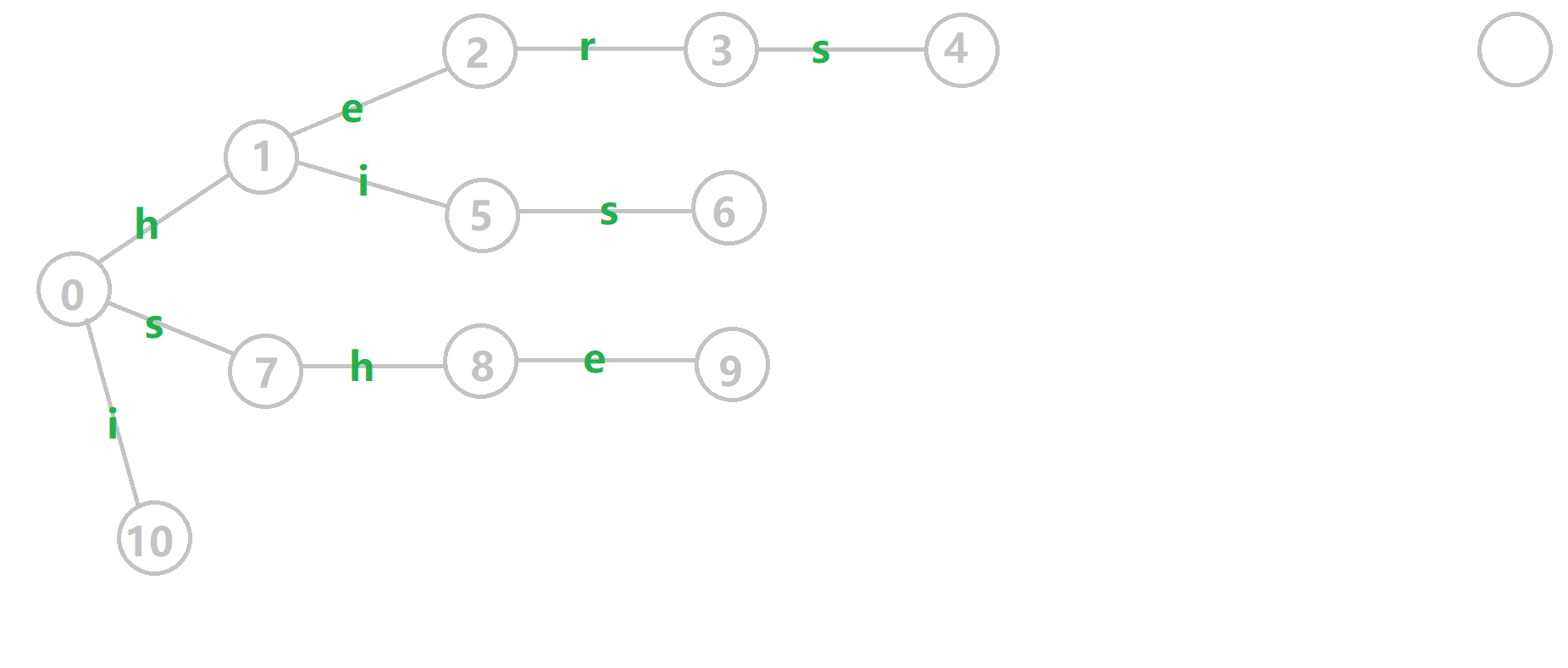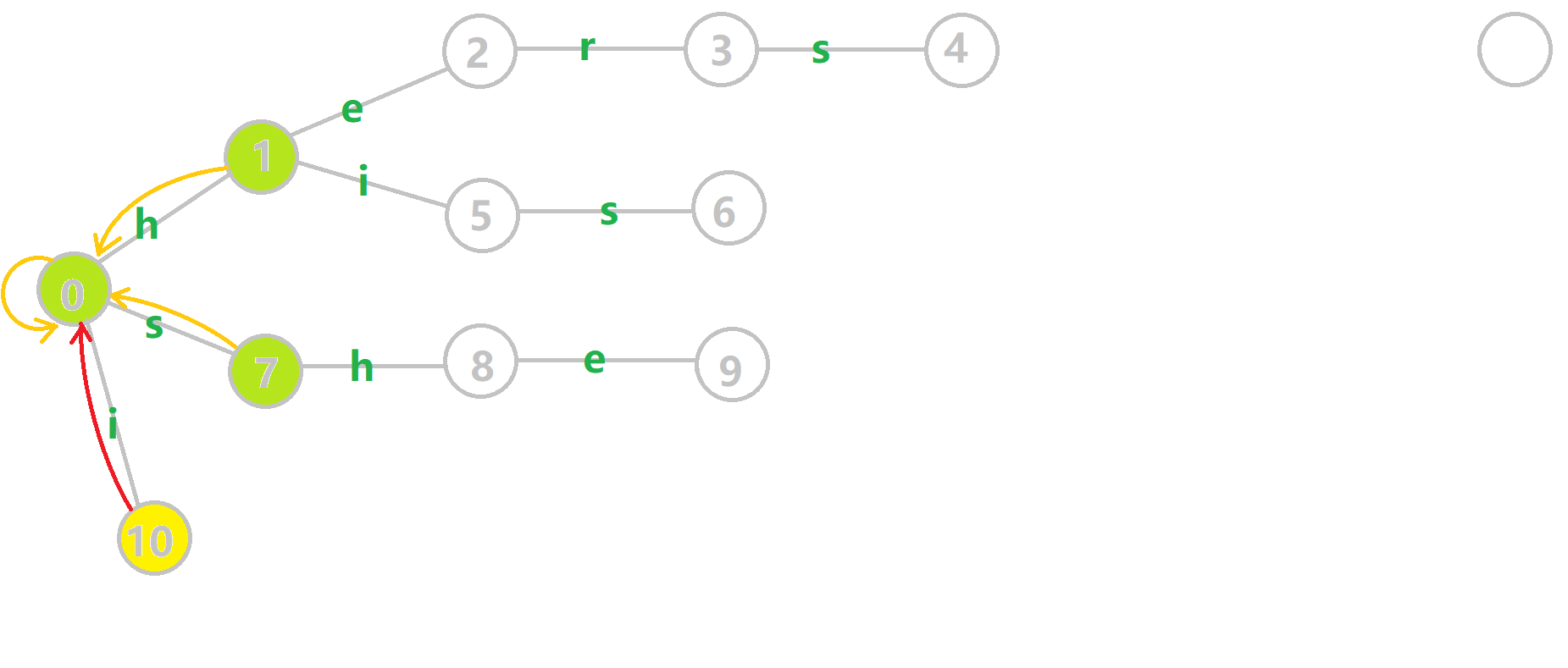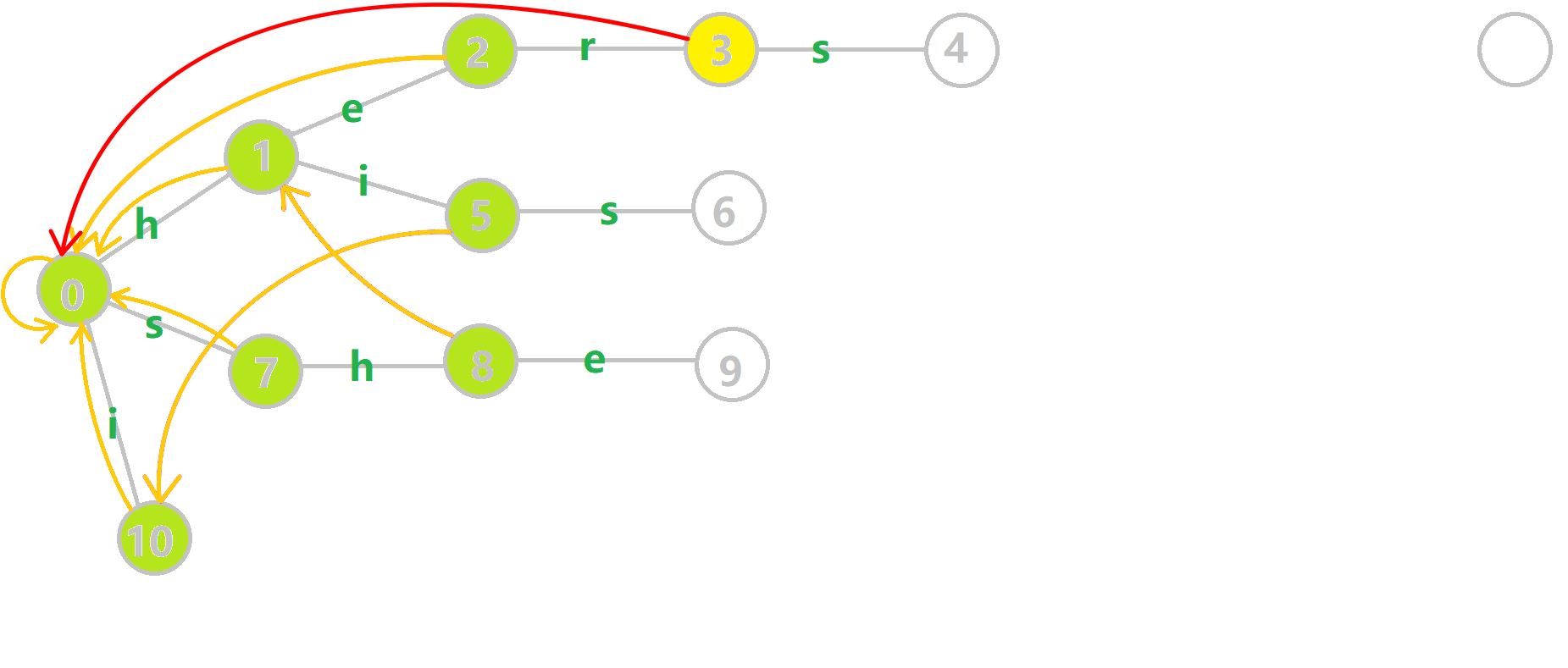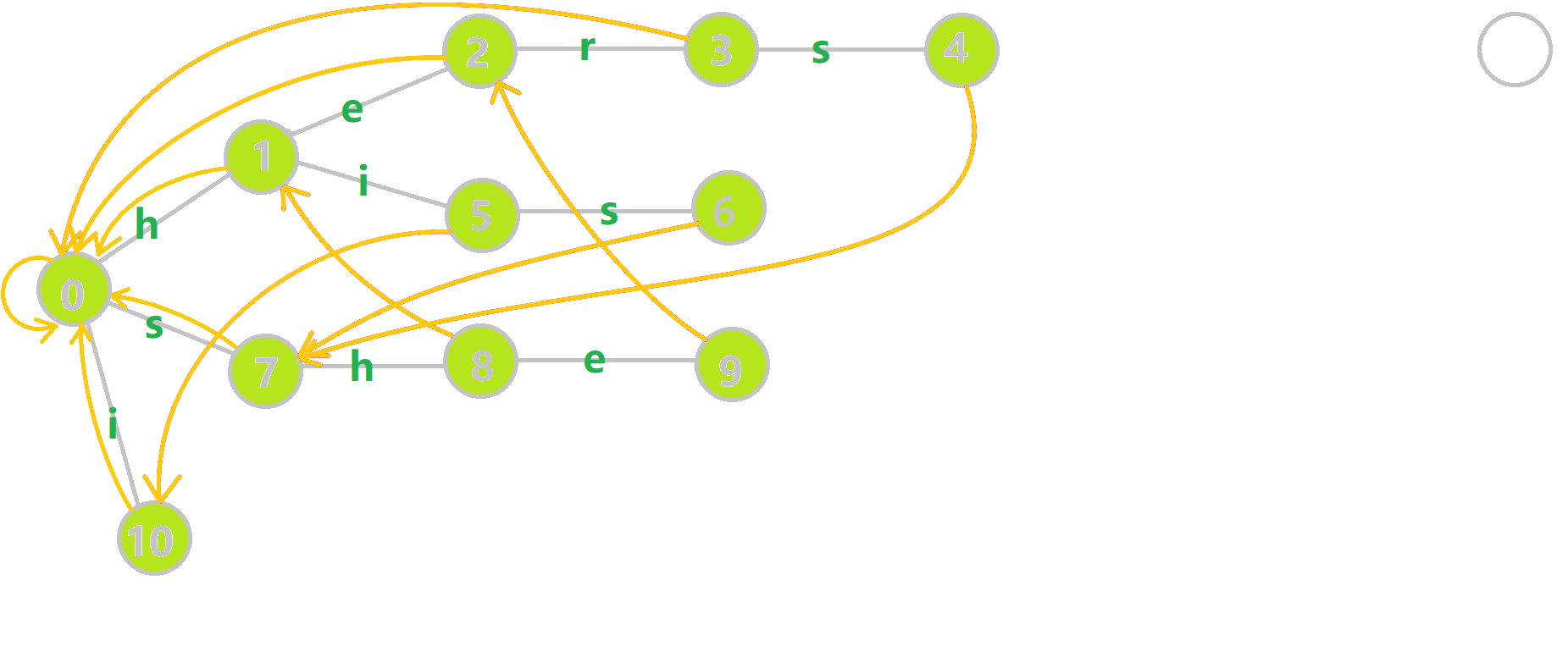
- 黄色结点：当前的结点
- 绿色结点：表示已经 BFS 遍历完毕的结点
- 橙色的边：已确认的失配指针
- 红色的边：当前求出的失配指针
以结点 6 的失配指针添加为例讲解具体构建的细节：
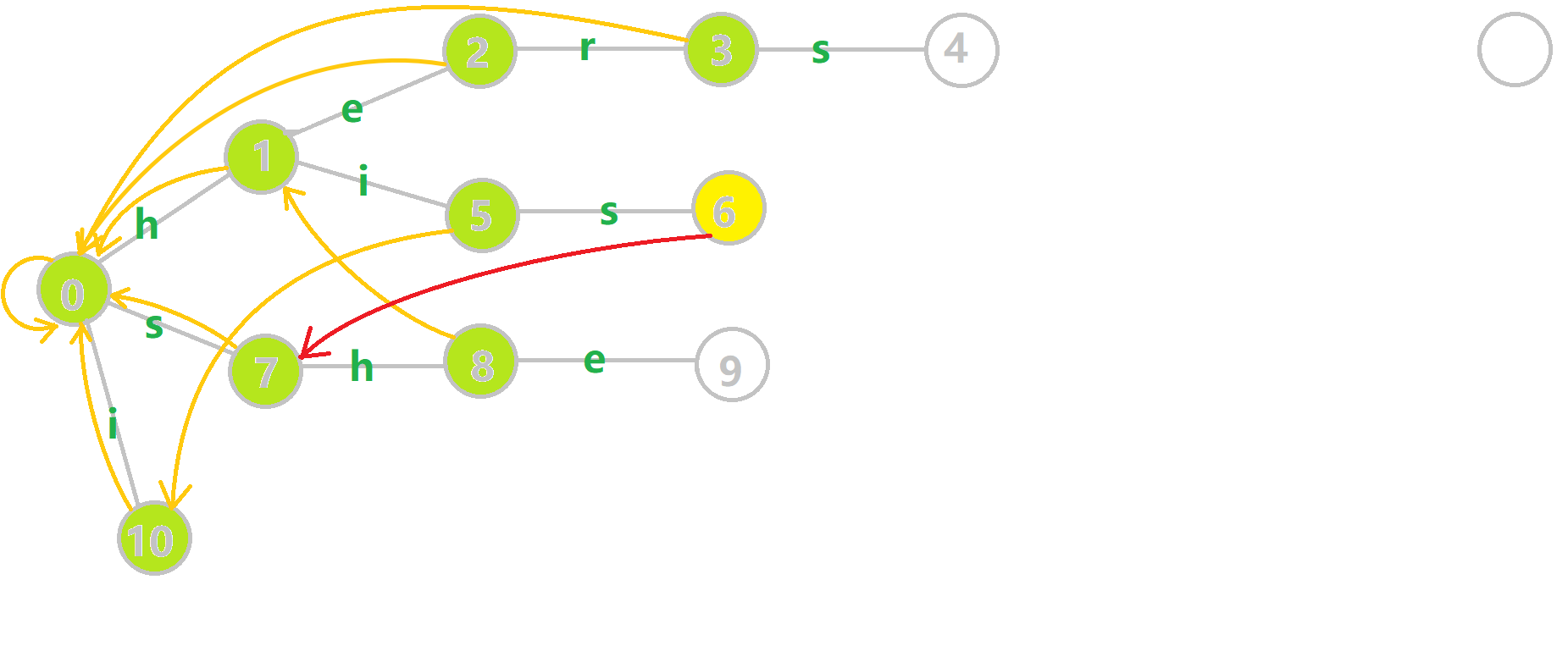
- 先找到结点6的父结点5的失配指针，$fail[5]=10$，由于结点10的子结点与结点6不存在相同的最小后缀（不存在边是
s的情况），所以继续寻找结点10的失配结点，$fail[10]=0$，结点0的子结点7与结点6存在相同的最小后缀s，所以$fail[6]=7$
添加完失配指针的最终结果如下：
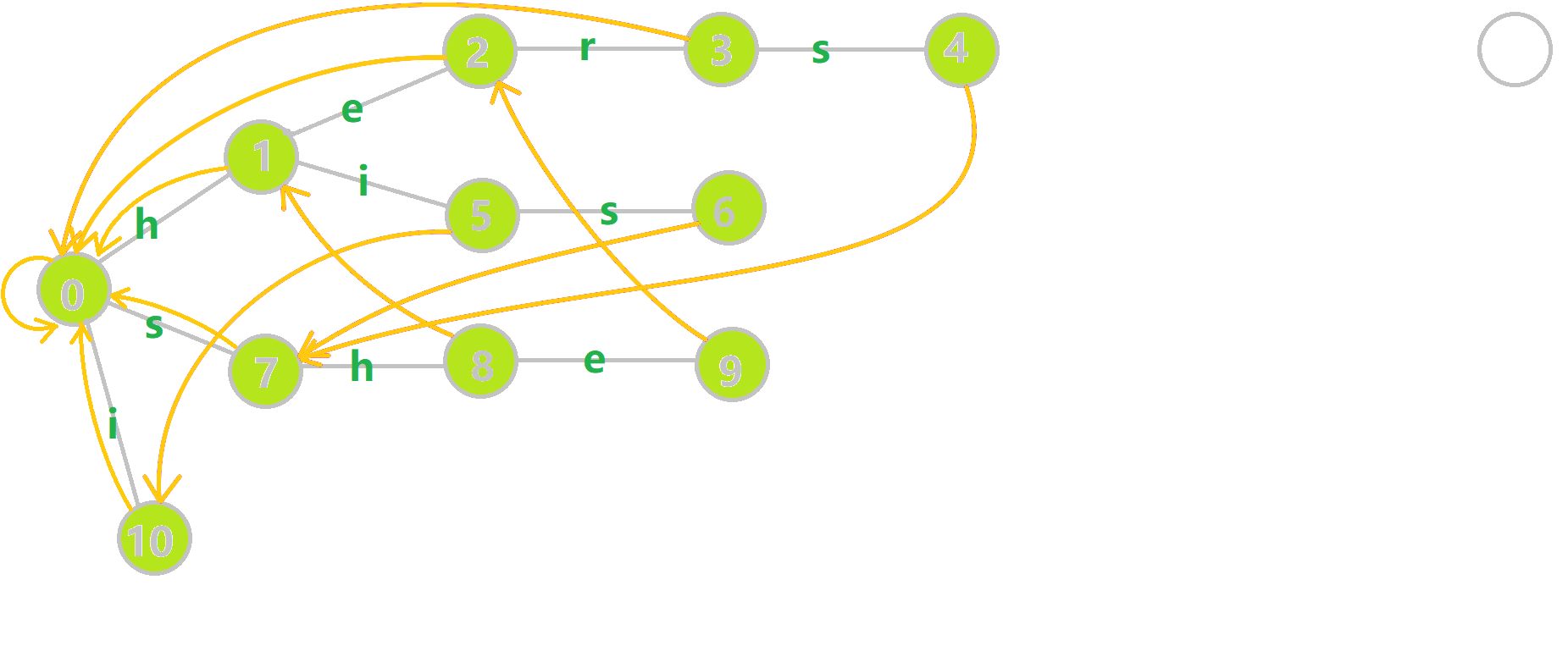
需要注意的是，此时的失配指针可能需要多次跳转才能找到最终的正确指针。通过将字典树转换为字典图，可以记录历史的信息，省略多次跳转的情况，具体可参考OI Wiki - 字典树与字典图
4 多模式匹配
和KMP算法是类似的，只不过AC算法是把被查询字符串放入由多个查询字符串构建的自动机中，进行遍历查询，当出现失配的情况时，将直接根据失配指针跳转到另一个与当前状态的后缀重合度最高的状态，并尝试继续匹配子结点，直到再次失配或遍历结束。
本章主要参考自OI Wiki - AC 自动机