1 数据操作
1.1 基础入门
- 理解数据、元素个数(size)、高维矩阵与维度(shape)
- 通过索引
[]与切片:来灵活读取高维矩阵 - reshape改变形状与矩阵初始化(zeros,ones)
1.2 运算符
- 按元素(elementwise)运算(加减乘除)
- 线性代数运算(向量点积、矩阵乘法)
- 张量连结(concatenate):按行(轴-0)/按列(轴-1)
1.3 广播机制
广播机制(broadcasting mechanism)的工作方式:通过适当复制元素来扩展一个或两个数组, 以便在转换之后,两个张量具有相同的形状。
比如说一个$3\times1$的矩阵和一个$1\times2$的矩阵相加,由于他们形状不匹配,所以会对第一个矩阵列复制,第二个矩阵行复制,最终结果为$3\times2$的矩阵
1.4 节省内存
有的操作可能会导致为新结果分配内存
before = id(Y)
Y = Y + X
id(Y) == before
# False
Pytorch可以通过X[:] = X + Y或X += Y实现原地修改,以减少操作的内存开销
TensorFlow提供了tf.function修饰符用于减少计算的内存开销
1.5 类型转换
torch张量和numpy数组将共享它们的底层内存
A = X.numpy()
B = torch.tensor(A)
type(A), type(B)
# (numpy.ndarray, torch.Tensor)
a = torch.tensor([3.5])
a, a.item(), float(a), int(a)
# (tensor([3.5000]), 3.5, 3.5, 3)
tensorflow转换后的结果不共享内存
A = X.numpy()
B = tf.constant(A)
type(A), type(B)
# (numpy.ndarray, tensorflow.python.framework.ops.EagerTensor)
a = tf.constant([3.5]).numpy()
a, a.item(), float(a), int(a)
# (array([3.5], dtype=float32), 3.5, 3.5, 3)
2 数据预处理
- 数据读取
pd.read_csv - 缺失值处理
fillna和哑变量处理get_dummies(df, dummy_na=True) - 复杂的缺失数据可根据具体情况选择插值法和删除法
3 线性代数
- 标量(仅包含一个数值)
- 向量(标量值组成的列表)
- 矩阵(一阶向量组成的二阶向量)
- 张量(描述具有任意数量轴的$n$维数组的通用方法)
重点概念:
矩阵的转置、线性变换、矩阵乘法、哈达玛积(Hadamard product,也就是矩阵的点积)、矩阵的Frobenius范数(元素的平方和再开方,类似于矩阵的$L_2$范数)、对称与反对称矩阵、矩阵的正定(特征值大于零,性质上类似复数中的正实数)、正交矩阵(行向量和列向量皆为正交的单位向量)、置换矩阵(特殊的正交矩阵,向量由一个1和多个0组成)、特征向量、特征值
按特定轴求和,维度为[2,3,4,5]的张量,按照axis=[1,3]求和后,最后的维度为[2,4]。而通过设置参数keepdims=True,最后的维度为[2,1,4,1]。
4 微积分
重点概念:
斜率、导数、微分法则(常数、加法、乘法、除法)、链式法则、亚导数(拓展不可微的函数求导)、偏导、梯度(将导数拓展到向量)、矩阵求导

拓展资料:
矩阵求导的本质与分子布局、分母布局的本质(矩阵求导——本质篇):https://zhuanlan.zhihu.com/p/263777564
矩阵求导公式的数学推导(矩阵求导——基础篇):https://zhuanlan.zhihu.com/p/273729929
矩阵求导公式的数学推导(矩阵求导——进阶篇):https://zhuanlan.zhihu.com/p/288541909
5 自动微分
5.1 计算图
深度学习框架通过构建一个计算图(computational graph)来加快求导,并实现自动计算导数,即自动微分(automatic differentiation)。
计算图的构建:
- 将代码分解成操作子
- 将计算表示成一个无环图
- 显式构造(Tensorflow/Theano/MXNet)
- 或 隐式构造(PyTorch/MXNet)
自动求导的两种模式:正向累积VS反向累积

实际情况下,反向累积优于正向累积
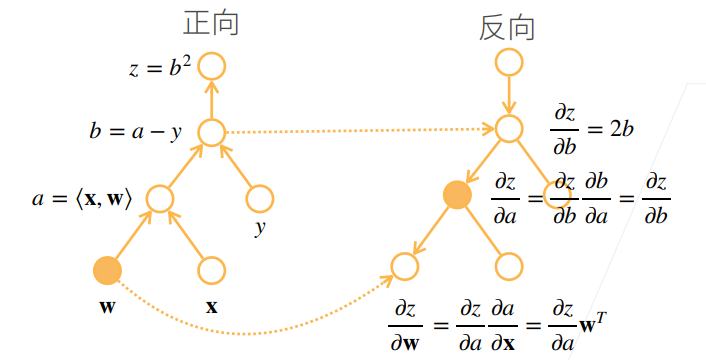
5.2 反向累积
反向累积过程:
- 构造计算图
- 正向执行,存储每个操作子的结果
- 反向累积,借助中间存储和链式法则,计算每个操作子的梯度
复杂度分析
- 反向累积的计算复杂度是O(n),n表示操作子个数
- 反向累积的内存复杂度是O(n),正向的n个中间存储,这也是实际运行神经网络需要耗费较大的显存资源的原因
- 正向累积的内存复杂度是O(1),因为不需要存储中间结果
- 但正向累积的计算复杂度非常高,每个变量的梯度都需要O(n)的计算复杂度
- 相比于正向累积,反向累积借助空间换时间的思想,实现了更高效的综合表现
5.3 自动微分的示例(PyTorch)
import torch
x = torch.arange(4.0)
x.requires_grad_(True)
# 等价于x=torch.arange(4.0,requires_grad=True)
y = 2 * torch.dot(x, x)
y.backward()
x.grad
# tensor([ 0., 4., 8., 12.])
# 在默认情况下,PyTorch会累积梯度,我们需要清除之前的值
x.grad.zero_()
y = x * x
u = y.detach() # 分离出与y值相同的变量u
z = u * x # 反向传播时,u将被看作常数
z.sum().backward()
x.grad == u
# tensor([True, True, True, True])
5.4 自动微分的示例(Tensorflow)
import tensorflow as tf
x = tf.range(4, dtype=tf.float32)
x = tf.Variable(x)
# 把所有计算记录在磁带上
with tf.GradientTape() as t:
y = 2 * tf.tensordot(x, x, axes=1)
x_grad = t.gradient(y, x)
x_grad == 4 * x
# <tf.Tensor: shape=(4,), dtype=bool, numpy=array([ True, True, True, True])>
# 设置persistent=True来运行t.gradient多次
with tf.GradientTape(persistent=True) as t:
y = x * x
u = tf.stop_gradient(y)
z = u * x
x_grad = t.gradient(z, x)
x_grad == u
# <tf.Tensor: shape=(4,), dtype=bool, numpy=array([ True, True, True, True])>
t.gradient(y, x) == 2 * x
# <tf.Tensor: shape=(4,), dtype=bool, numpy=array([ True, True, True, True])>
6 概率基础
重点概念:
事件、抽样、分布、大数定律、联合概率、条件概率、贝叶斯定理、概率求和/边际化、独立与依赖、期望和方差/标准差
7 查阅文档
- 调用
dir函数查看属性 - 调用
help函数查看说明 - 在Jupyter记事本中使用
?和??