1 斐波那契数列
在文章开始之初，首先为大家介绍一个新生物，那就是斐波那契兔子。
斐波那契兔子是一种很神奇的物种，这种兔子寿命很长，而且具备很固定的繁殖周期和繁殖能力。每一只小兔子都需要经历一个月的成长周期变成大兔子，而每一对大兔子在坠入爱河后，都会历经一个月的生育周期繁衍出一对小兔子。
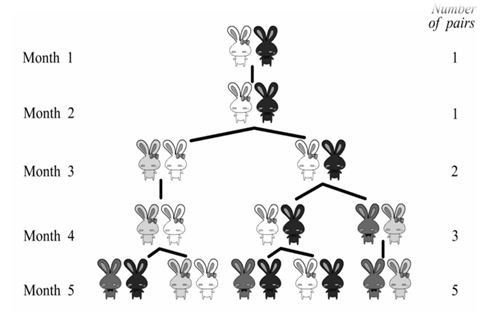
这么来看的话，如果第一个月有1对小兔子，那第二个月就会有1对大兔子，而第三个月又会出现2对兔子（一对是大兔子，一对小兔子）。以此类推，那么等到第五个月，就会出现5对兔子了。
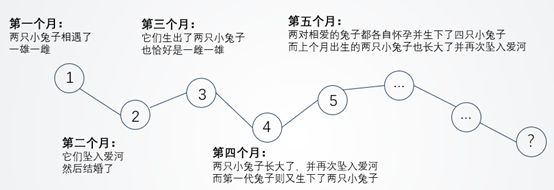
那么问题来了，10年后，到底有多少对相爱的兔子呢？
假设月份数为n，那么问题的规律在于，当n>3时：
第n月的兔子夫妻数 = 第n-1月的兔子夫妻数 + 第n-2月的兔子夫妻数
以此类推，经过简单的计（bian）算（cheng）可得：
10年后（即240个月后）会有8670007398507948658051921对兔子！
大老师的碎碎念：
现在一共有约 8.67*10^24__对兔子。假设一对兔子爪牵爪有40cm远，则这么多兔子爪牵爪的话：
- 可绕地球赤道8.65*10^16圈；
- 可绕地球公转轨道3.69 *10^12圈；
- 可来回牛郎织女星约11456140次
下面大老师来给大家介绍一下这个斐波那契兔子疯狂的兔子的创造者：列奥纳多·斐波那契。
中世纪意大利数学家，是西方第一个研究斐波那契数的人，并将现代书写数和乘数的位值表示法系统引入欧洲。著有《计算之书》等书。
斐波那契大师通过兔子繁殖的例子定义了这样一个数列：1，1，2，3，5，8，13，21， 34，55……这被称为斐波那契数列。这个数列从第3项开始，每一项都等于前两项之和。被包含在斐波那契数列中的数也被称之为斐波那契数，而引出数列的例子中提及的兔子也被称为斐波那契兔子。
这个简单而又特别的定义，赋予了斐波那契数特殊的规律和魅力。比如连续斐波那契数的平方和可以转为成两个斐波那契数的乘积，具体如下图所示：
除此之外在无限延伸的斐波那契数列上，还会有其他的很多神奇的规律：
神奇的循环
最后一位数字，每60个数一循环； 最后两位数字，每300个数一循环； 最后三位数字，每1500个数一循环； 最后四位数字，每15000个数一循环； 最后五位数字，每150000个数一循环，等等。
神奇的整除
每第三个数可被2整除； 每第四个数可被3整除； 每第五个数可被5整除； 每第六个数可被8整除，等等。 这些除数本身也属于斐波那契数列
斐波那契数列的内在规律暗合自然界中的物质变动、生物分化的规律，因此在现实生活中存在着许许多多和斐波那契数息息相关的现象。比如，树木的生长分叉和山脉河流的分支都暗合斐波那契的增长规律，而常见的花瓣数量也往往是一个斐波那契数。
- 与树木的分叉规律对应
- 与山脉的俯视分支对应
- 与花瓣的常见数量对应
这些往往难以被察觉的细节都在无形中表现出了自然的瑰丽，或许大自然才是将数学应用到鬼斧神工的地步的大艺术家吧！
2 黄金螺旋线
上一节我们讲到数学中的斐波那契数，那么这一期让我们将数字转化为图形，更加直观地感受一下数学的黄金精神吧。
首先我们先以斐波那契数列为基础，绘制长度为斐波那契数的简单正方形。结果如下：
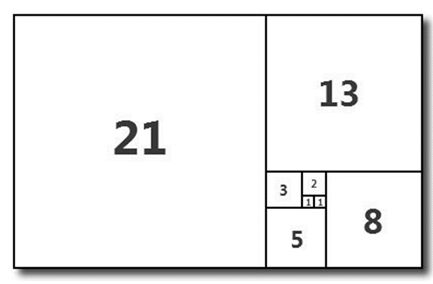然后我们按照斐波那契数列的顺序依次用一条曲线连接这些正方形，神奇的事情发生了！
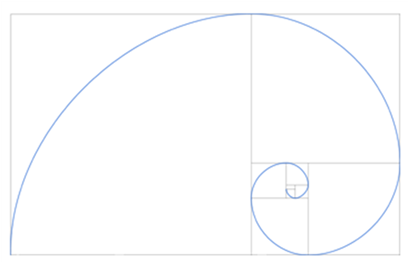最优雅的非对称图形——黄金螺旋线突然出现！有没有感觉有点眼熟？
没错，大自然中存在着许许多多的黄金螺旋线，这是大自然的又一个神奇之处。
从数学的角度进行严格定义的话，黄金螺旋线其实是等角螺线。而所谓的等角螺线，指的是臂的距离以几何级数递增的螺线。设 L 为穿过原点的任意直线，则 L 与等角螺线的相交的角A永远相等，这是等角螺线最重要的性质，也是“等角”一词的由来。
利用定义中的“臂的距离以几何级数递增”这一点，我们可以很轻松地绘制等角螺线：
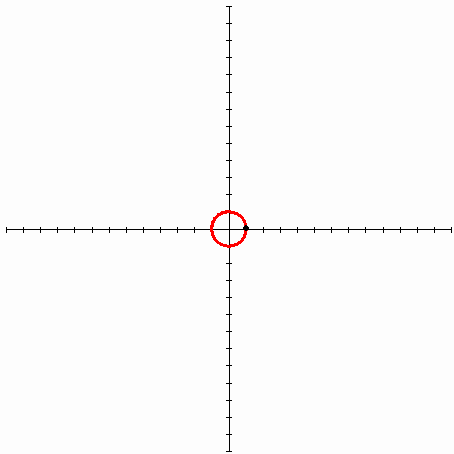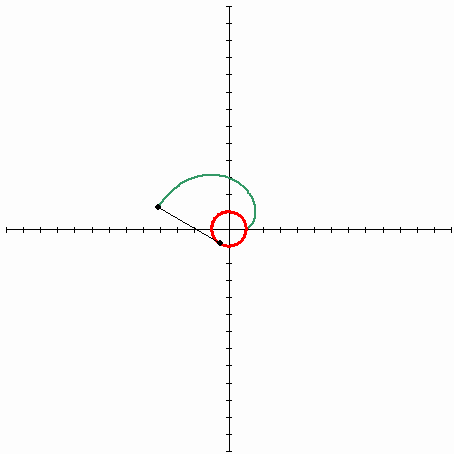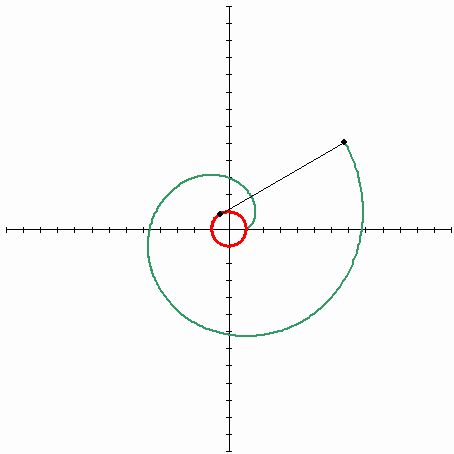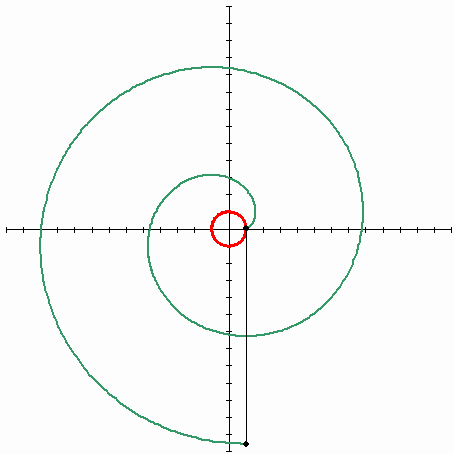
值得一提的是，我们需要把等角螺线和等速螺线区分开，等速螺线是一个点匀速离开一个固定点的同时又以固定的角速度绕该固定点转动而产生的轨迹，又称阿基米德线。听不懂没关系，看下图就一目了然了：
放错了，嘿嘿，其实是下面这个图（其实没啥区别）
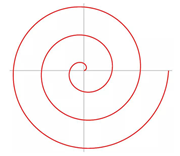
大老师的碎碎念：
著名数学家雅各布 · 伯努利就是等角螺线的一个狂热爱好者，并在临死前决定把等角螺线作为自己的墓志铭，但是可惜的是为他雕刻墓碑的工匠可能对等角螺线和等速螺线分不太清楚，所以最终在墓碑上刻下了等速螺线，在此对伯努利大师表示深深的同情。
言归正转，黄金螺旋线不仅在动植物上有所体现，在更广阔的大海，更深邃的宇宙中也都蕴含着美妙的黄金螺旋线。
从一个小小的蜗牛，到一个小池里的漩涡
从整个海洋的洋流，再到这个大大的宇宙
宇宙的本质，或许我们仍未可知
但肯定的是，他的本质一定很美
从斐波那契数列到黄金螺旋线，我们对于数学的黄金精神的探索再次迈出了重要的一步。或者那小小的斐波那契数背后还蕴藏着更深的秘密~
3 黄金分割比
本次我们来聊一聊一个大名鼎鼎的比例，那就是传说中最能引起美感的比例——黄金分割比。黄金比例是一个定义为 (√5-1)/2的无理数，约为0.618。这是一个非常有趣的比例，这个比例不仅仅常见于诸如音乐、绘画、雕塑、建筑等艺术领域，而且在管理、工程设计等方面也有着不可忽视的作用。
我们也可以通过一个简单的数学公式来得到这个比例：
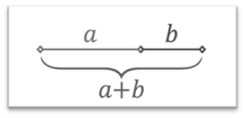
仔细分析公式，我们可以很轻松的在现实中得到黄金分割比。也就是说如果将一根绳切分成a、b两段，然后保证较短段（b段）与较长段（a段）的比值等于较长段（a段）与整段（a段+b段）的比值，那我们就对这根绳进行了黄金分割，分割的比例也就是黄金分割比。
大老师的碎碎念：
传说在古希腊时期，毕达哥拉斯（著名数学家、哲学家，开创了毕达哥拉斯学派）在马路上散步，在经过铁匠铺时听见了铁匠打铁的声音并感觉十分悦耳。于是他驻足倾听，然后发现铁匠打铁的节奏很有规律。这个声音的节奏最终被毕达哥拉斯用数学的方式表现了出来，那就是黄金比例，即我们上文提及的黄金分割比例。果然，伟大的人在马路上散步也会有灵感~
黄金分割比例是一个很玄学的比例：
音乐：二胡演奏中，“千金”分弦的比符合0.618∶1时，奏出来的音调最和谐、最悦耳
科学：在很多科学实验中，选取方案常用一种0.618法，即优选法，它可以使我们合理地安排较少的试验次数找到合理的西方和合适的工艺条件。
经管：资产-负债率（即负债总额除资产总额）应以黄金分割点为临界点，如果高于这个点就可能面临较大经营风险
心理：人的脑电波图,若高低频率比为1：0.618时,乃是身心最具快乐欢愉之感的时刻
可能有些说法或许仍有待求证，但不可否认黄金分割比例在很多领域都是一个经常提及的概念。而且最为有趣的是，黄金分割比例和我们之前讨论的斐波那契数列（没看过之前文章的读者请下拉至最低，点击查看相关的系列文章）息息相关。
斐波那契数列是1 1 2 3 5 8 13 21 34 55…… 我们依次用后一项除以前一项，可以得到这样一个结果： 1÷2=0.5， 2÷3=0.666...， 3÷5=0.6， 5÷8=0.625， …………， 55÷89=0.617977…， ………… 144÷233=0.618025…
仔细观察，能发现这个结果在逐渐逼近0.618，也就是黄金比例。通过对斐波那契数列的简单处理，我们居然就可以得到的黄金分割比。斐波那契数列再一次彰显了他的神奇之处！
黄金比例在美学领域有着举足轻重的地位，并对仪表姿态、绘画构图、礼乐音律、建筑雕塑等领域提出了清晰合理的美学规范
奥黛丽赫本的面貌存在着多处黄金比例
芭蕾舞者通过踮起脚尖是的上下身呈现黄金比例
巴黎埃菲尔铁塔多处分段呈现黄金比例
帕特农神庙结构的长宽比呈现黄金比例
很多人反对黄金比例在美学领域的运用，因为他们觉得审美不应该是有公式可以标准化的。或许有的美是个性化的，是独有的美，是不可公式化的。但有的美是可以达成共识的，是可以分享，是可以融合了一些数学的瑰丽血脉。或许，我们已经看到了属于数学的黄金精神的一角了吧！
4 伟大的渺小
黄金比例很简单，因为它只代表着一个简单的数值；黄金比例也可以很复杂，因为自然的本质也可能是一个很简单的东西。
当简单的黄金比例遇到简单的圆时，又会发生哪些奇妙的化学反应呢？
黄金角137.5°——圆与黄金分割比碰撞的魅力360°✖0.618
单看黄金角或许会让人有些迷惑，毕竟这好像只是一个普普通通的角度。但是这个角度一旦和黄金比例有关联，那它或许就没那么简单啦~
以上的几幅图都蕴含着黄金角，你看出来了吗？
蕴含着黄金角度的几何体在旋转的过程中也会产生一种难以言喻的美感。
思维的跨越与融合往往能让1+1迸发出大于2的力量！
一个例子：三分之四是什么？三分之四+圆+旋转 这又可以产生什么？
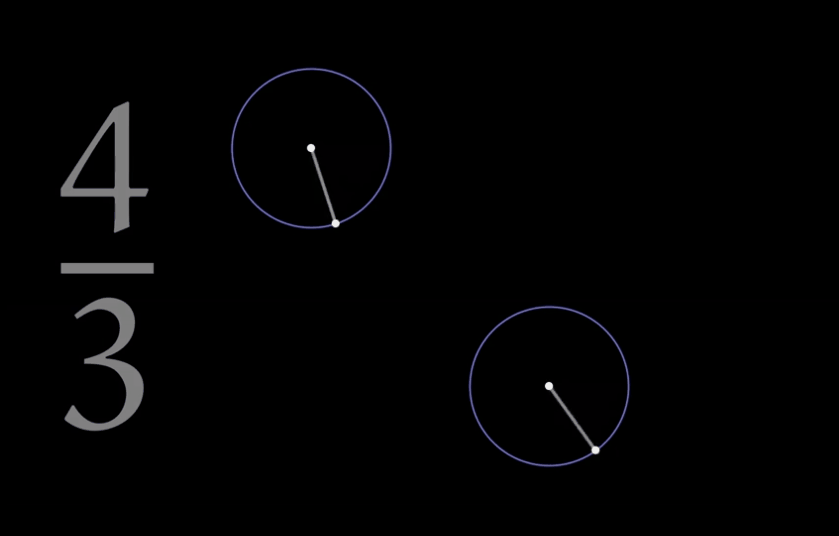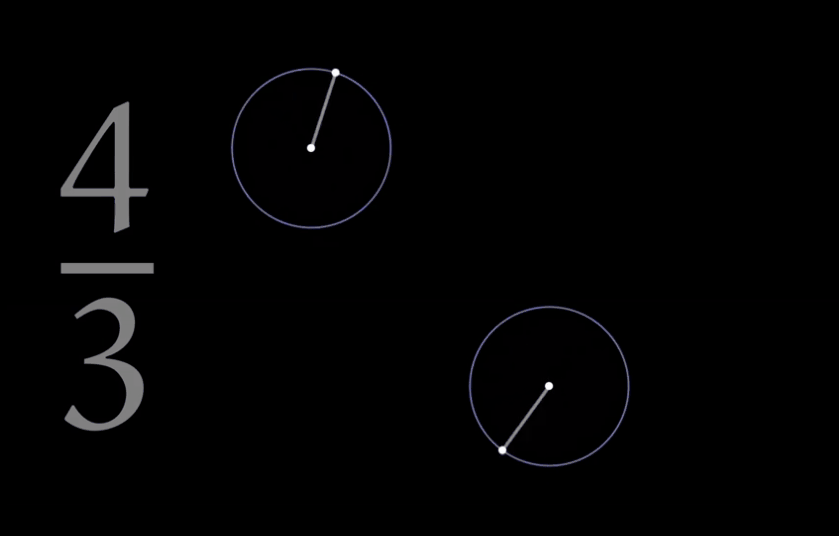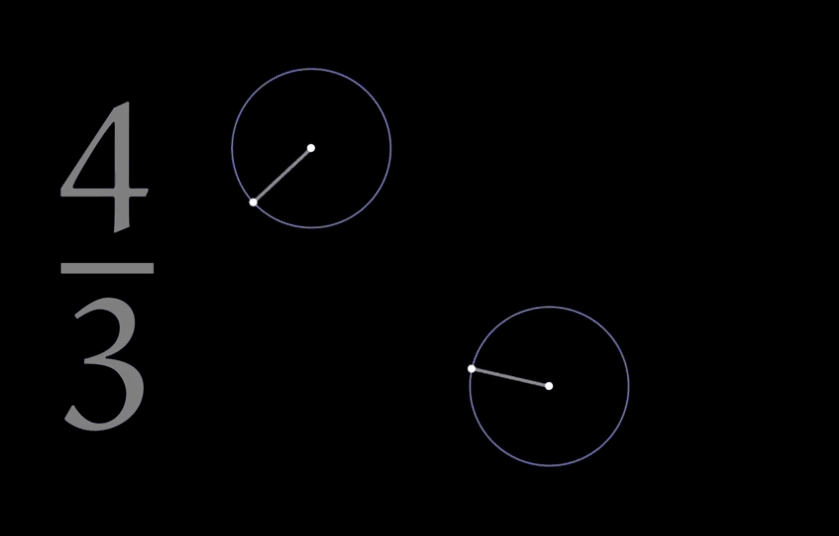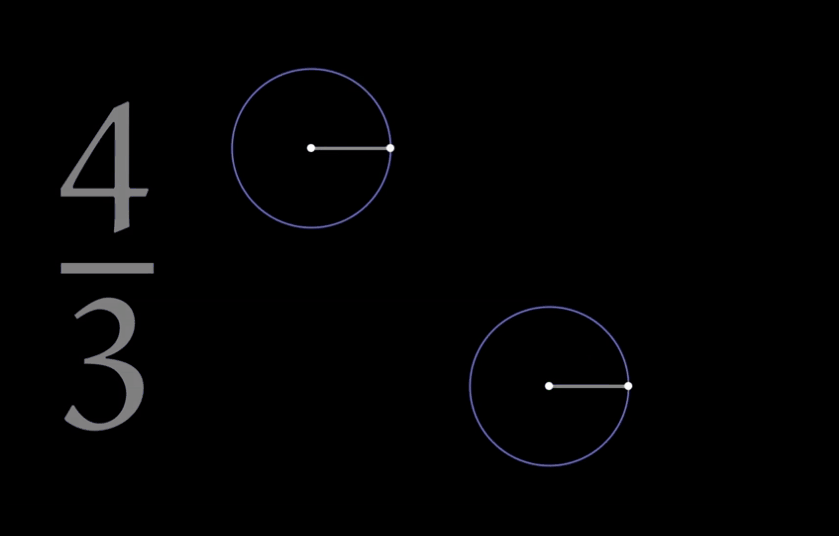
你是否想过一个简单的三分之四还可以如此美丽
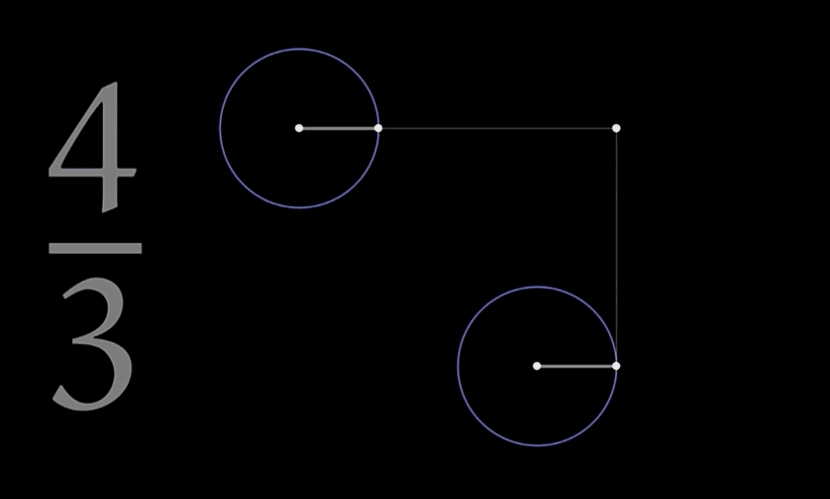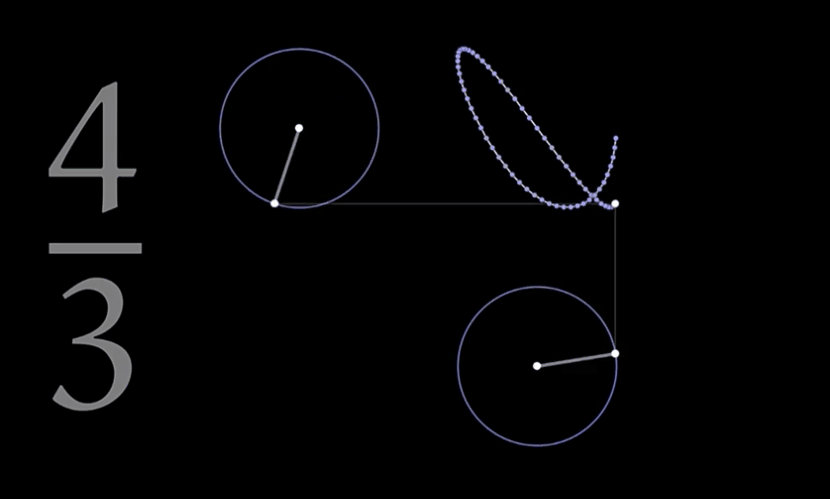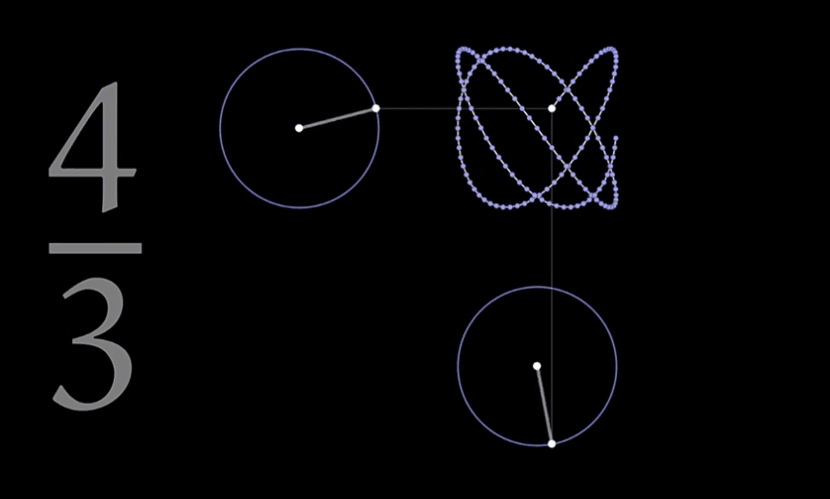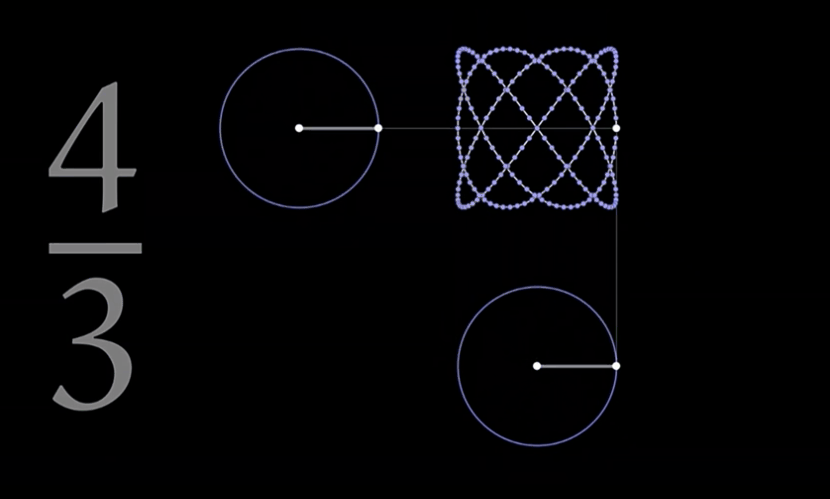
当生命意识到宇宙奥秘的存在的时候，距它最终解开这个奥秘的就只有一步之遥了 ——《朝闻道》
如果把地球的历史浓缩成24小时，那么人类就只在最后的3秒钟才出现。 ——《人类简史》
自然的伟大之处在于他天然的具有一种无与伦比的规则美 人类的伟大之处在于他在学习自然的伟大，并尝试超越他 永恒的黑夜里，突然一丝光芒撕开了宁静。那是无意中得到一丝开化的智人，从一开始人类的崛起之路已经势不可挡。 第一次绘制图案、第一次点燃火把、第一次发明文字、第一次建立文明、第一次工业革命、第一次电脑诞生、第一次你过生日，一代代人对世界的探索，最终在无数次的失败后人类逐渐摸索出一条相对安全的路。 前人的一番开拓成就了后来者的更进一步，在漫长的时间里我们一步一步看似缓慢实则坚定的步伐中前进，到如今我们再回首却发现原来已经走了这么远，原来已经爬的这么高。
原来这数学中的黄金精神是指那个敬畏而求知的渺小，是指那个懂得融合和成长的渺小，是指那个懂得质疑和超越的渺小，是指那个逐渐走向伟大的渺小。