1 KMP 算法概况
KMP,全称为Knuth-Morria-Pratt,是三位创始人的名称凑出来的
KMP 算法是一种字符串匹配算法,时间复杂度 :O(n+m)
特性:字符串头部和尾部会有重复的部分,利用这部分信息,减少匹配次数
理解字符串的前缀和后缀
- 把字符串切割成非空的两份,前面那份就是前缀,后面那份就是后缀
- 所有前缀的可能性组成了前缀集合,所有后缀的可能性组成了后缀集合,比如”Harry”的前缀集合是{”H”, ”Ha”, ”Har”, ”Harr”},而”Potter”的后缀集合是{”otter”, ”tter”, ”ter”, ”er”, ”r”}
2 部分匹配表 PMT
KMP 算法的核心是部分匹配表(Partial Match Table),PMT 中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。
以字符串“abababca”为例,它的PMT如下:
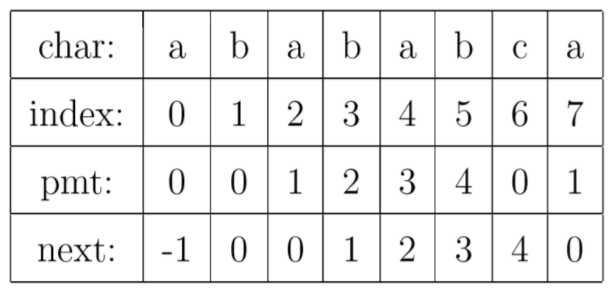
理解PMT值的计算
- 比如当$index=4$的时候,对应的字符串为$ababa$
- 前缀集合为{”a”, ”ab”, ”aba”, ”abab”},后缀集合为{”baba”, ”aba”, ”ba”, ”a”}
- 集合交集为{”a”, ”aba”},因此$value_{pmt}=len(aba)=3$
- $next$值是$pmt$值平移的结果,为了方便后续的使用
3 应用 PMT 加速匹配
举例:用字符串 B=“abababca”匹配字符串 A=“ababababca”:
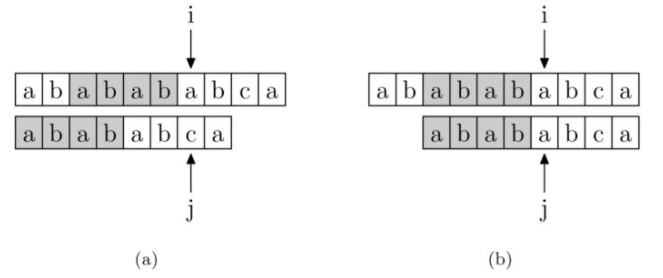
- 在 $index=0$ 处开始匹配,当匹配到 $index=j$ 时,匹配失败
- 暴力枚举法会从 $index=1$ 处重新开始匹配
- 而 KMP 算法则会根据 $index=j$ 时的 $next$ 值,推论出字符串 A 已匹配部分 $index=[0,j-1]$ 中存在后缀与字符串 B 的前缀一致,都是“abab”(图中灰色部分)
- “abab”也就是字符串“ababab”的前缀集合与后缀集合的交集中最长元素
- 下一轮匹配的起点将是 $index=j-next_j=6-4=2$,并且由于“abab”是已经匹配好的,所以后续的匹配判断将直接从 $index=i$ 开始