1 数值积分示例
题目:用数值积分法求解$\int_1^2 \frac{dx}{x}$
先用普通方法计算积分的精确结果(用于精度比较):
$$\int_1^2 \frac{dx}{x}=lnx|_1^2=ln2\approx0.693147$$
然后使用辛普森公式进行近似值求解:
- 选择最简单的近似求解,此时$\Delta x=\frac{1}{2},n=2$
- 涉及三个坐标$(1,1),(\frac{3}{2},\frac{2}{4}),(2,\frac{1}{2})$
- 最终结果$\frac{\Delta x}{3}(y_0+4y_1+y_2)=\frac{1}{6}(1+4\frac{1}{3}+\frac{1}{2})\approx0.69444$
- 此时数值计算结果和真实值的误差为$(\Delta x)^4$
2 积分计算示例
题目:计算$y=e^{-r^2}$函数曲线下的面积为$Q=\int_{-\infty}^{\infty}e^{-r^2}dr$
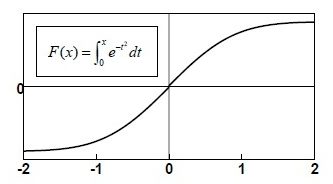
- 设函数 $F(x)=\int_0^xe^{-t^2}dt$,则$Q=2F(\infty)$,由此将积分计算问题转化为对面积的求解
- 设$y=e^{-r^2}$函数图像绕$y$轴旋转一周后的旋转体体积为$V$
- 则根据壳层法可得:$V=\int_0^{\infty}2\pi re^{-r^2}dr=\pi$
- 通过选择不同的$b$,可以利用平面$y=b$对旋转体进行分割,如下图左侧
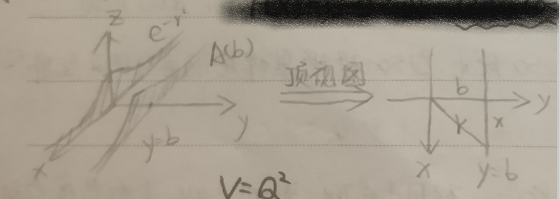
分割过程细节补充(妙啊~)
- 每次通过平面$y=b$分割旋转体都会得到一个截面,设截面的面积为$A(b)$
- 从顶视图(俯视图)的角度来看,设截面上任意点与$z$轴的距离为$r$,则$r^2=b^2+x^2$
- 由于旋转体是由函数$y=e^{-r^2}$绕$y$轴旋转所得,所以面积$A(b)=\int_{-\infty}^{\infty}e^{-r^2}dx$
- 面积$A(b)$的化简:$A(b)=\int_{-\infty}^{\infty}e^{-b^2}e^{-x^2}dx=e^{-b^2}Q$
- 考虑圆盘法的逆向过程,则所有截面的面积加和应该等于旋转体的体积
- 即$V=\int_{-\infty}^{\infty}A(y)dy=\int_{-\infty}^{\infty}e^{-y^2}dyQ=Q^2$
- 最终解析分割过程,得出结论$V=Q^2$,即$Q=\sqrt{V}=\frac{\sqrt{\pi}}{2}$
3 Unit 3 知识点简单概括
截止到第二十三节课,本课程的第三单元:积分入门(Unit 3 Intro to Intergration)部分内容已完成,内容脉络简单梳理如下:
- 定积分的定义与求解(面积近似法)
- 微积分基本定理(FTC1、FTC2、换元法)
- 定积分的应用(圆盘法、壳层法、功、概率)
- 定积分的数值计算(黎曼和、梯形法、辛普森公式)
4 参考
