1 主流神经网络架构
An overview of the main types of neural network architecture
1.1 前馈神经网络
Feed-forward neural networks
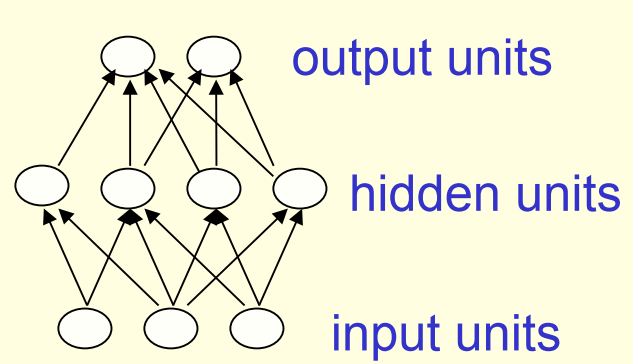
- 当隐藏层层数大于1时,即为”深度“神经网络
1.2 循环神经网络
Recurrent networks
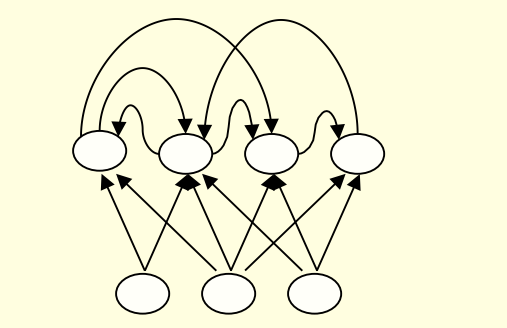
- 在神经网络的图结构中包含有向环
- 多用于处理时序数据,输入数据可以不定长
- 2011年Ilya Sutskever就利用RNN实现了具备可读性的文本生成
1.3 对称连接网络
Symmetrically connected networks
- 单元之间的连接是对称的
- 两个方向上权重共享
- 往往服从某种能量分布 并且存在诸多限制
- 没有中间隐藏层的对称连接网络也被称为Hopfield网络
受限波尔兹曼机Boltzmann machines
- 存在隐藏层的对称连接网络
- 性能上一般优于Hopfield网络,但弱于RNN
- 具有简洁优美的学习算法,具体将在后续课程说明
本课程比较老(2012年),所以不涉及诸如Transform等新架构
2 第一代神经网络:感知器
Perceptrons: The first generation of neural networks
2.1 感知器 Perceptrons
标准感知器结构:
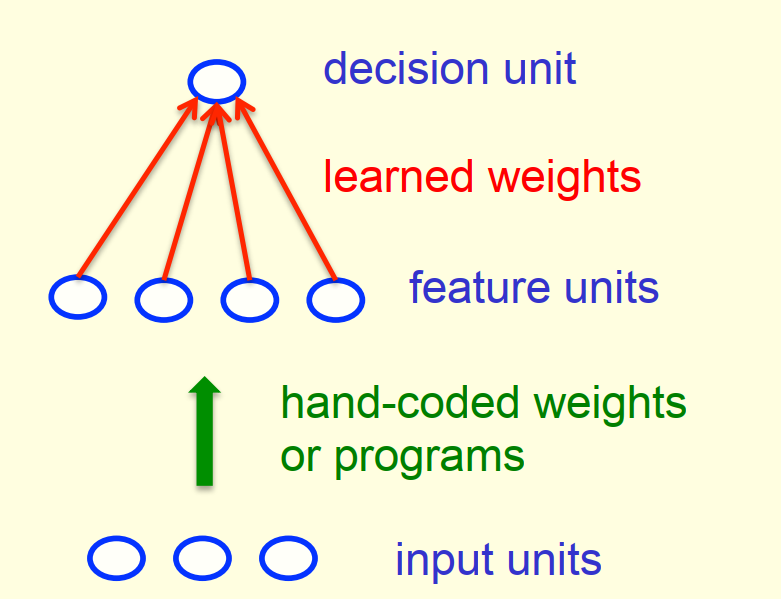
感知器历史:
- 19世纪60年代由Frank Rosenblatt推广
- 1969年,由Minsky和Papert出版《感知器(Perceptrons)》一书,书中介绍了感知器相关应用和局限性,而这些局限性至今仍存在于诸多神经网络模型中
- 感知器至今仍广泛应用于存在百万特征向量的学习任务中
感知器一般采用 Binary threshold neurons 作为基础神经元
2.2 训练过程思路
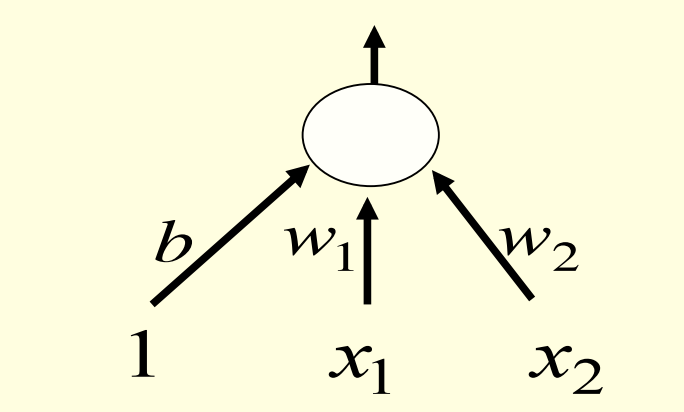
如何学习偏差项(biases)
- 偏差项可以看作$x_i=1$的特殊情况
- 在每层神经元的输入部分新增一个恒为1的输入
- 神经网络就会自然学习到偏差项的估计值
权重的学习:
- 如果输出结果正确,则权重不变
- 如果输出结果错误且为0,则权重向量应该”加上“输入向量,使得模型结果向1修正
- 如果输出结果错误且为1,则权重向量应该”减去“输入向量,使得模型结果向0修正
3 感知器的几何解释
A geometrical view of perceptrons
3.1 权重空间 Weight-space
权重空间的定义
- 权重向量的每一个值表示权重空间的一个维度
- 权重空间的每一个点表示权重向量的一个可能性
- 通过平移消除掉偏差项,确保每一个训练样本都可以表示为一个过原点的超平面
- 权重向量必须位于超平面的某一侧才能表示预测正确
3.2 权重空间的理解
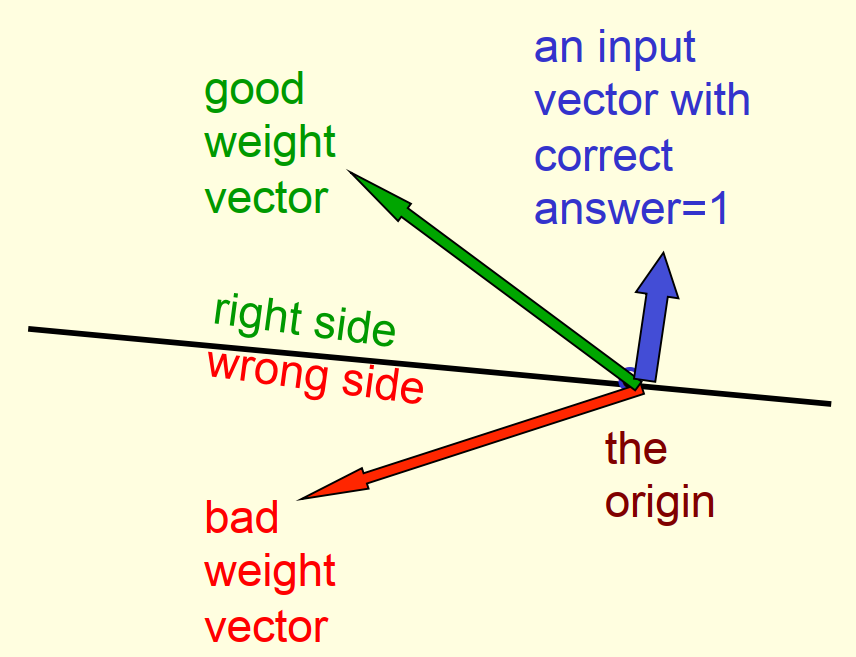
- 蓝色表示输入的特征向量,对应的真实值为1
- 当权重向量和特征向量完全平行时,结果为正,表示预测正确
- 将特征向量作为法线确定一个过原点的黑色超平面
- 超平面的一侧包含了所有预测正确的权重向量
- 超平面的另一侧包含了所有预测错误的权重向量
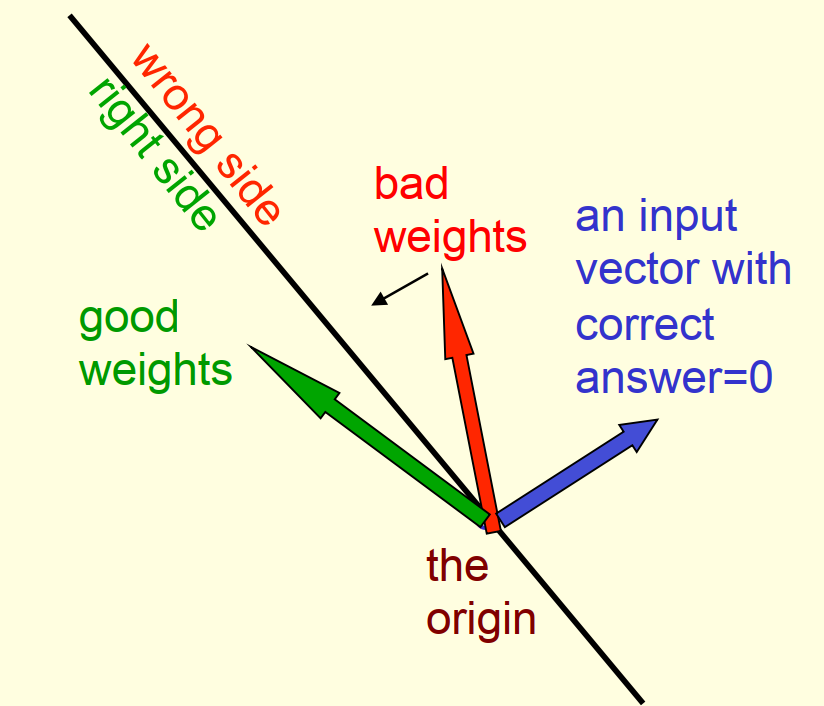
- y=1时与特征向量在同一侧的权重向量一定输出正确
- y=0时与特征向量在不同侧的权重向量一定输出正确
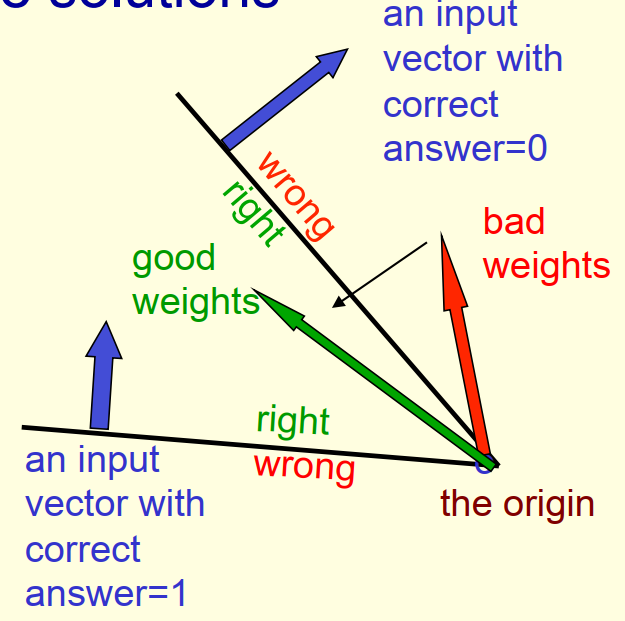
- 每个训练样本都对应一个超平面
- 这些超平面分割出来的一个权重正确空间和一个权重错误空间
- 感知机训练算法就是要找到所有权重正确空间的交集,也就是“夹角”内的某个权重向量。
- 该权重向量能使感知机对尽可能多的训练样本都输出正确的预测结果
- 如果两个权重向量是可行,那么夹在它们中间的那些向量一定也可行,说明这是个convex问题。
4 感知器的可行性分析
Why the learning works
Every time the perceptron makes a mistake, the learning algorithm moves the current weight vector closer to all feasible weight vectors
by Hopeful claim
再次回顾感知机权重向量$v$的训练算法
对任意训练实例$(x,y)$,其中$y=1$或$0$,假设特征向量为$f$:
- 若$y=1$,则$v += f$
- 若$y=0$,则$v -= f$
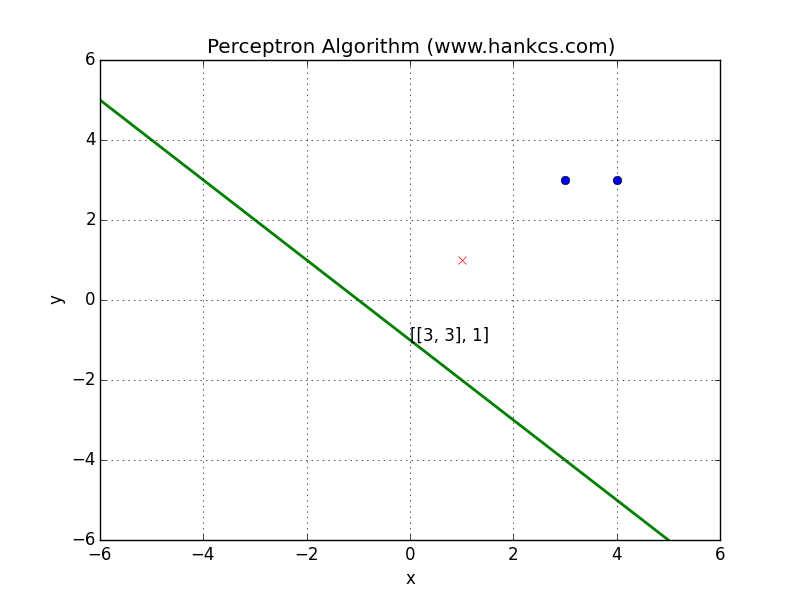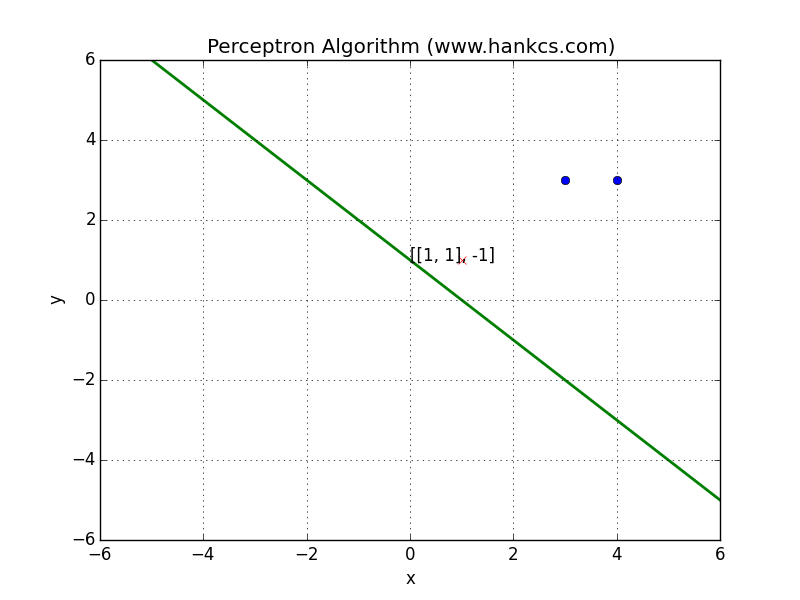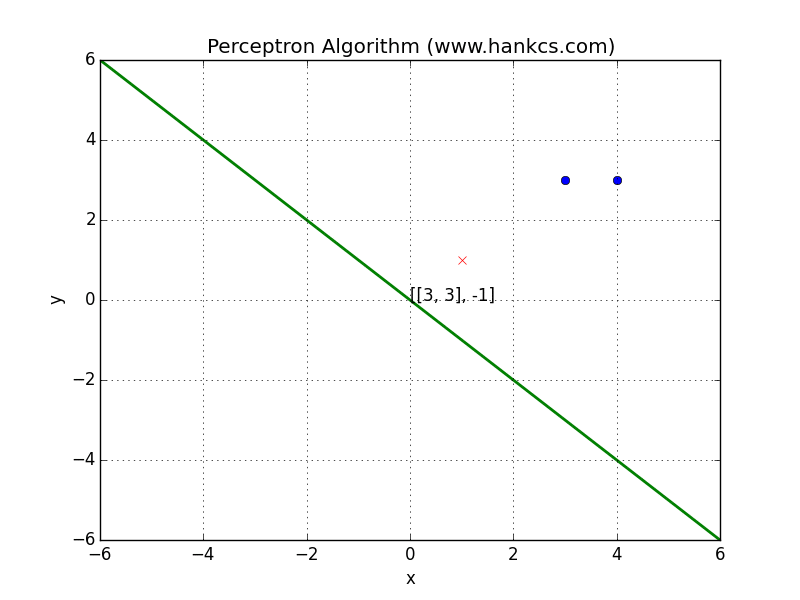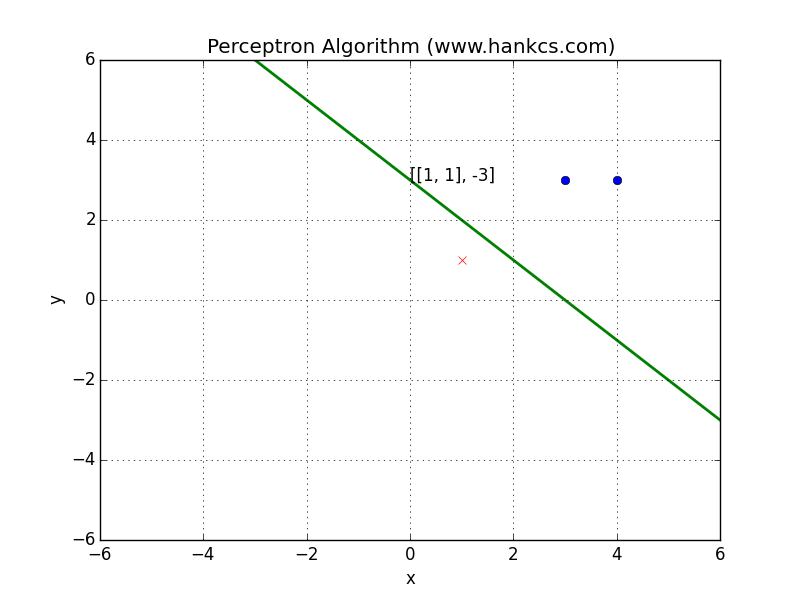
此训练方法在weight space中的解释如下:
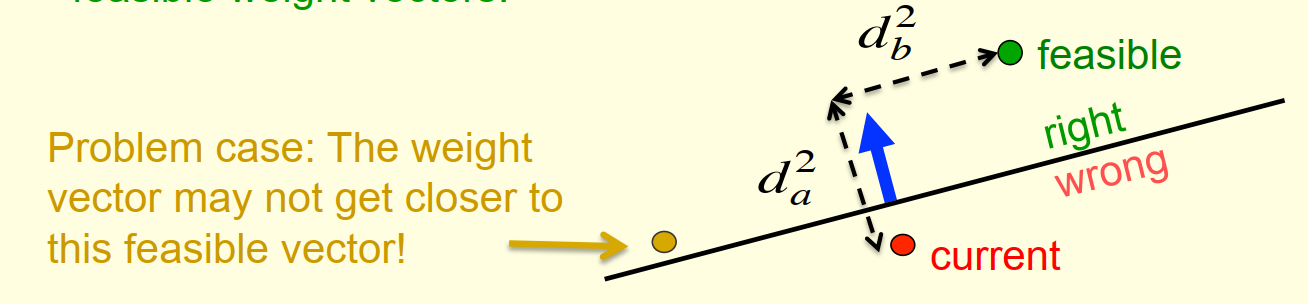
- 绿点表示最优的权重向量,红点表示当前的权重向量,蓝线表示特征向量
- 训练的目标是让红点逐渐逼近绿点,定义目标函数为两者的
squared distance - 但如果当前权重向量是橙点(
Problem case),则意味着模型结果将会变得更差 - 因为输入的特征向量会导致橙点对应的权重向量更新后,目标函数变大
- 所以需要一个限制,通过定义一个有限制的权重向量最优解,将橙色点排除在外
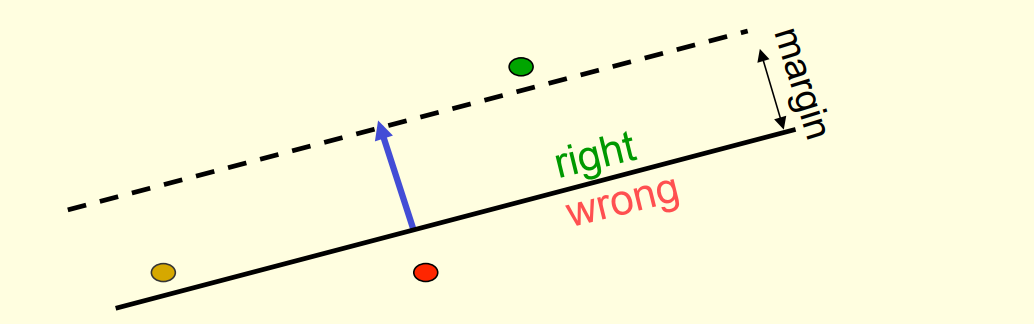
- 定义$margin$为特征向量的长度
- 限制可行参数解距离超平面的距离必须大于等于$margin$
- 这样就确保可行参数解不再只是实线以上的部分,而是虚线以上的部分
- 橙点也会因此被排除掉
收敛性证明的非正式概述:
- 当前案例为$y=1$,预测结果为$0$
- 感知器预测错误,所以执行权重更新 $v += f$
- 红点将沿着蓝线移动,使得目标函数减少
- 目标函数减少值 = $margin^2$
- 因此在经历有限次的模型错误和权重更新
- 目标函数将会收敛逼近0而得到最优解(前提是存在最优解)
5 感知器的局限性
What perceptrons can’t do
如果特征选得好,感知机几乎可以做任何事情。
但如果特征选得不好,造成数据看上去线性不可分,那么感知机就懵逼了。
5.1 XNOR门
感知器当初被人诟病最多的地方就在于它甚至不能解决XNOR门的问题
XNOR门的问题图示:
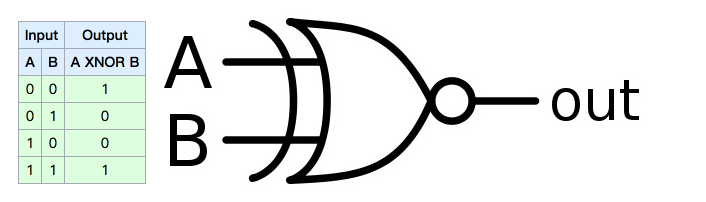

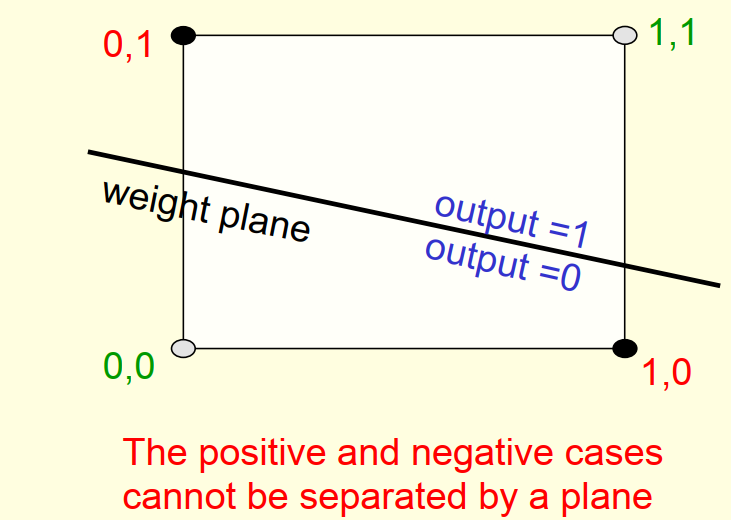
以上公式对于感知器来说是无解的:
5.2 一维图像的模式识别
感知器也很难直接区分以下两种模式
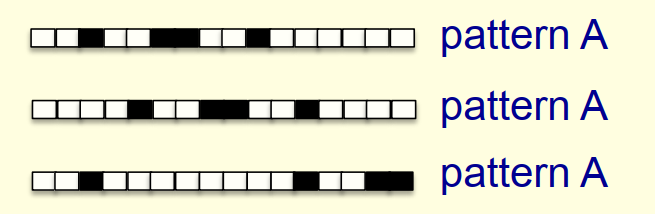
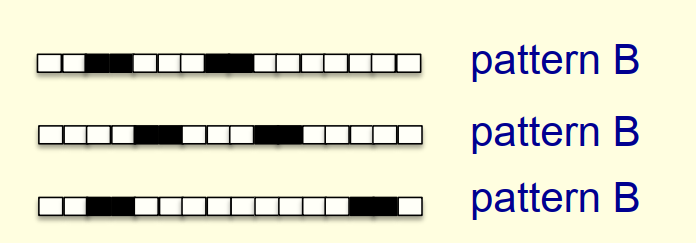
原因分析:
- 假设黑色像素对于1,白色像素对应0,则输入特征为元素为0或1的向量
- 所有符合patternA的样本集合相加 = 所有符合patternB的样本集合相加
- 因此两份样本最终更新所得的权重向量也是一致的,最终感知器进入懵逼模式
这些弱点是导致早期神经网络和感知器被人忽视的原因
但是合理的特征构建,依然能让感知器发挥出很大的效果
而后来的隐藏层,实现了特征的自动表达,也使得神经网络焕发出别样的光彩