支持向量机(support vector machine,简称为SVM)
- 作为经典的有监督学习算法,常用于分类与回归分析问题中
- 支持向量机有着完备而优雅的数学理论,并且计算成本低效果好
- 在集成学习与深度学习流行前,SVM 在很多领域都是非常主流的算法
SVM 算法图解:
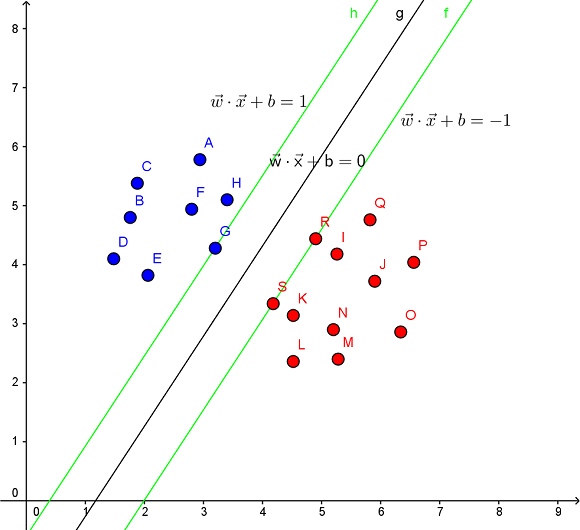
- SVM 核心思想在于通过寻找一个超平面,尽可能的分隔不同类别间的样本
- 支持向量(support vector):用于确定超平面边缘的部分样本
SVM 借助核技巧将输入隐式映射到高维特征空间中,从而有效地进行非线性分类
常见的核函数:
| 核函数 | 表达式 | 备注 |
|---|---|---|
| Linear Kernel线性核 | $k(x,y)=x^{t}y+c$ | |
| Polynomial Kernel多项式核 | $k(x,y)=(ax^{t}y+c)^{d}$ | $d\geqslant1$为多项式的次数 |
| Exponential Kernel指数核 | $k(x,y)=exp(-\frac{\left |x-y \right |}{2\sigma ^{2}})$ | $\sigma>0$ |
| Gaussian Kernel高斯核 | $k(x,y)=exp(-\frac{\left |x-y \right |^{2}}{2\sigma ^{2}})$ | $\sigma$为高斯核的带宽,$\sigma>0$, |
| Laplacian Kernel拉普拉斯核 | $k(x,y)=exp(-\frac{\left |x-y \right |}{\sigma})$ | $\sigma>0$ |
| ANOVA Kernel | $k(x,y)=exp(-\sigma(x^{k}-y^{k})^{2})^{d}$ | |
| Sigmoid Kernel | $k(x,y)=tanh(ax^{t}y+c)$ | $tanh$为双曲正切函数,$a>0,c<0$ |
SVM 算法优缺点分析:
- 理论基础好,具备非线性分类能力;追求结构化风险最小,泛化能力强
- 最终决策函数由少数的支持向量决定,鲁棒性强,避免了“维数灾难”
- 针对凸优化问题可以发现全局最优解,可以避免过拟合的问题
- 适用于小样本学习方法,但对大规模训练样本难以实施
- 不容易处理多分类问题,对数据缺失敏感,对部分超参的选择敏感
关于 SVM 算法的对偶问题和推导过程 #待补充