中文标题:FactorVAE: 基于变分自编码器的概率动态因子模型,用于预测横截面股票收益
英文标题:FactorVAE: A Probabilistic Dynamic Factor Model Based on Variational Autoencoder for Predicting Cross-Sectional Stock Returns
发布平台:AAAI
Proceedings of the AAAI Conference on Artificial Intelligence
发布日期:2022-06-28
引用量(非实时):
DOI:10.1609/aaai.v36i4.20369
作者:Yitong Duan, Lei Wang, Qizhong Zhang, Jian Li
关键字: #FactorVAE
文章类型:journalArticle
品读时间:2024-02-04 17:15
1 文章萃取
1.1 核心观点
FactorVAE,作为噪声建模具有固有随机性的概率模型。本质上,我们的模型将机器学习中的动态因子模型(DFM)与变分自动编码器(VAE)相结合,提出了一种基于 VAE 的先验后验学习方法,可以通过逼近最优后验因子来有效指导模型的学习具有未来信息的模型。
特别是,考虑到风险建模对于噪声股票数据很重要,FactorVAE 除了预测收益之外,还可以估计 VAE 潜在空间上的分布方差。对真实股市数据的实验证明了FactorVAE的有效性,其性能优于各种基线方法
1.2 综合评价
- 本文模型设计新颖,通过融合 DFM 与 VAE 实现了对股票横截面的有效建模
- FactorVAE 的回测效果很好,但美中不足的是缺少不同经济周期下表现的验证
- 对市场和非市场的划分较为模糊,未来可考虑融入的信息(比如文本或宏观指标)
1.3 主观评分:⭐⭐⭐⭐⭐
2 精读笔记
2.1 背景知识
已有方案的限制:股票数据的信噪比低
- 大量噪声数据会干扰基于机器学习的模型的学习,并导致模型提取的潜在因素的有效性较差
因素模型(Factor Model)的分类:
- 静态因子模型,股票的暴露因子不随时间而变化,比如资本资产定价模型(CAPM)
- 动态因子模型,股票的暴露因子随时间而变化,通常根据公司或资产特征(例如市值、账面市值比、资产流动性)计算得出;非线性因子模型一般性能会更好
动态因子模型(DFM)的一般函数形式:$y_s=\alpha_s+\sum_{k=1}^K\beta_s^{(k)}z_s^{(k)}+\epsilon_s$
- 其中 $y_s$ 表示 $N$ 只股票在经过时间步长 $s$ 后的横截面收益
- $\alpha_s$ 表示这组股票的特异性回报(idiosyncratic returns,即独立于市场的收益波动部分)
- $\beta_s$ 表示因子暴露矩阵;$z_s$ 表示 K 个因子向量;$\epsilon_s$ 表示零均值的特殊噪声
对于参数为 $\Theta$ 的动态因子模型,可表示如下:$\hat{y}_s=f (x_s;\Theta)=\alpha (x_s)+\beta (x_s) z (x_s)$
1_study/DeepLearning/生成式神经网络#变分自编码器 VAE
2.2 算法细节
FactorVAE 整体架构:
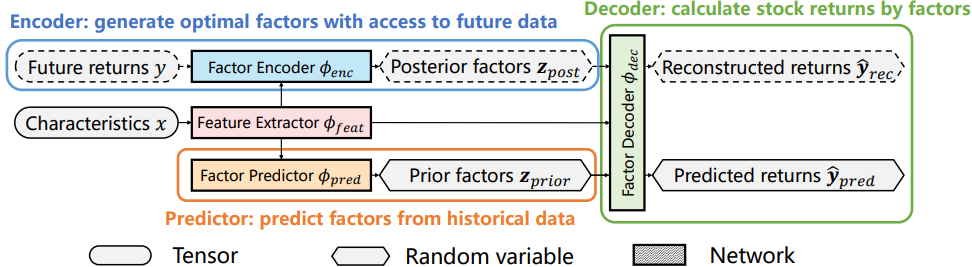
- 注意:虚线框住的模块表示未来的数据,仅在训练阶段使用,在测试或预测阶段不存在
- 该架构包含 4个组件:特征提取器、因子编码器、因子解码器和因子预测器
- 特征提取器使用 GRU 从历史序列特征 $x$ 中提取时刻 $T$ 时股票潜在特征 $e=h_{GRU}^T$
- 因子编码器从未来股票收益 $y$ 和潜在特征 $e$ 中提取后验因子 $z_{post}$:
$$ \begin{aligned}\mu_{post},\sigma_{post} &=\phi_{\mathrm{enc}}(y,e) \\z_{post}&\sim\mathcal{N}\left(\mu_{\mathrm{post}},\mathrm{diag}\left(\sigma_{\mathrm{post}}^{2}\right)\right)\end{aligned} $$
其中 $z_{post}$ 是服从独立高斯分布的随机向量,其均值为 $\mu_{post}$,标准差为 $\sigma_{post}$
- 因子解码器使用后验因子 $z$ 和潜在特征 $e$ 来计算股票收益 $\hat{y}$:
$$ \hat{\mathbf{y}}=\phi_{\mathrm{dec}}(\mathbf{z_{post}},e)=\mathbf{\alpha}+\mathbf{\beta}\mathbf{z_{post}} $$
- 因子预测器使用先验-后验学习(Prior-Posterior Learning)方法进行训练:因子预测器根据股票潜在特征 $e$ 输出预测因子(先验因子)$z_{prior}$,并尽可能地逼近最优后验因子 $z_{post}$:
$$ \begin{array}{l}[\mu_{\mathrm{prior}},\sigma_{\mathrm{prior}}]=\phi_{\mathrm{prod}}(e) \\\mathbf{z}_{\mathrm{prior}}\sim\mathcal{N}\left(\mu_{\mathrm{prior}},\mathrm{diag}\left(\sigma_{\mathrm{prior}}^{2}\right)\right)\end{array} $$
- 在预测阶段,因子预测器将输出预测因子,替代后验因子用于股票收益的预测:
$$ \hat{\mathbf{y}}_{\mathrm{pred}}=\phi_{\mathrm{dec}}(\mathbf{z}_{\mathrm{prlor}},x)=\boldsymbol{\alpha}+\beta\mathbf{z}_{\mathrm{prlor}} $$
由于因子解码器是对最终预测收益分布的评估,因此 FactorVAE 不仅可以用于预测股票的收益,还可以用于估计收益的波动性/风险。这在实际市场的投资中很有意义
整体流程梳理:
- 特征提取器输出的股票潜在特征 $e$ 会分别输出给因子编码器、因子解码器和因子预测器
- 因子编码器提取可访问未来数据的后验因子,因子解码器根据后验因子重建股票收益
- 因子预测器在训练阶段尽可能学习并逼近最优后验因子,在测试和预测阶段则替代因子编码器,为因子解码器提供可靠的预测因子,因子解码器根据预测因子重建股票收益
- 指导 FactorVAE 训练的目标函数包含两部分,第一个损失项是负对数似然比,追求减少后验因子重建收益的误差,第二个损失项是 KL 散度,追求预测因子和后验因子之间的分布尽可能的小
$$ \begin{gathered} L(x,y) =-\frac{1}{N}\sum_{\mathrm{i}=1}^{N}\log P_{\phi_{\mathrm{dec}}}\left(\hat{y}_{\mathrm{foc}}^{(i)}=y^{(i)}|x,\mathbf{z}_{\mathrm{posl}}\right) \\ +\gamma\cdot\mathrm{KL}\left(P_{\phi_{\mathrm{enc}}}\left(z|x,y\right),P_{\phi_{\mathrm{prod}}}\left(z|x\right)\right) \end{gathered} $$
算法细节 1:编码器与解码器的结构
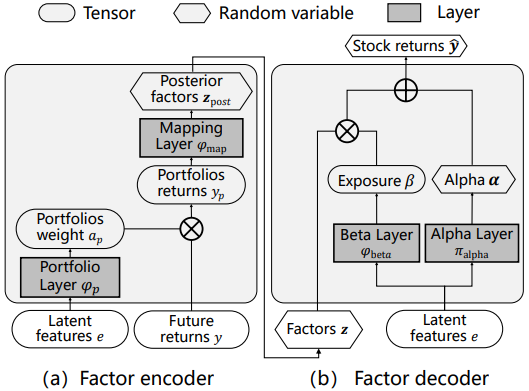
- 编码器的计算流程:潜在特征 $e$ 先经过函数 $\phi_p$ (线性变换+softmax)得到不同股票的权重 $\alpha_p$,之后一组股票未来收益 $y$ 加权后得到横截面收益 $y_p$(该方式规避了横截面内个股数据量大且动态变化的问题);映射层 $\phi_{map}$ 会计算得到后验因子 $z_{post}$ 的均值和标准差(用于后验因子的生成)
$$ \begin{aligned}\mu_{\mathrm{post}}&=w_{\mathrm{post}\mu}y_{\mathrm{p}}+b_{\mathrm{post}\mu} \\
\sigma_{\mathrm{post}}&=\text{Softplus}(w_{\mathrm{post}_{\sigma}}y_{\mathrm{p}}+b_{\mathrm{post}_{\sigma}})\end{aligned} $$
- 解码器的计算流程:该网络主要由 $\alpha$ 层与 $\beta$ 层组成
- (1)$\alpha$ 层根据潜在特征 $e$ 输出这组股票的特异性回报,即满足 $\alpha$ 分布的均值和标准差
$$ \begin{aligned} &h_{\alpha}^{(i)} =\text{LeakyReL.U}\left(w_{\alpha}e^{(i)}+b_{\alpha}\right) \\ &\mu_{\alpha}^{(i)} =w_{\alpha_\mu}h_\alpha^{(i)}+b_{\alpha_\mu} \\ &\sigma_{\alpha}^{(i)} =\text{Softplus}(w_{\alpha_\sigma}h_\alpha^{(i)}+b_{\alpha_\sigma}) \end{aligned} $$
- (2)$\beta$ 层先根据潜在特征 $e$ 输出因子暴露矩阵,然后根据动态因子模型(DFM)的公式 $y=\alpha +\beta z$ 得到横截面利润的分布 $\hat{y}\sim\mathcal{N}\left(\mu_{y}^{(i)},\sigma_{y}^{(i)^{2}}\right)$
$$ \begin{aligned} \beta^{(i)}&=\varphi_\text{beta}(e^{(i)})=w_\beta e^{(i)}+b_\beta \\ &\mu_{y}^{(i)} =\mu_\alpha^{(i)}+\sum_{k=1}^K\beta^{(i,k)}\mu_z^{(k)} \\ &\sigma_{y}^{(i)} =\left(\sigma_{\alpha}^{(i)^2}+\sum_{k=1}^{K}\beta^{(i,k)^2}\sigma_{z}^{(k)^2}\right)^{\frac{1}{2}} \end{aligned} $$
$\beta$ 层描述了市场相关因子引起的股价波动,$\alpha$ 层描述了独立于市场的其他股价波动
算法细节 2:因子预测器的结构

- 因子预测器使用一种多头全局注意力机制,以整合该因子的不同全局表征
- 多头注意力的结果会通过串联拼接在一起,之后使用和解码器中 $\alpha$ 层类似的结构来实现最终预测因子(先验因子)的输出;其中单个注意力头的计算方式如下:
$$ \begin{aligned} &k^{(i)} =w_\text{key}{ e }^{(i)},v^{(i)}=w_\textbf{value}{ e }^{(i)} \\ &a_{att}^{(i)} =\frac{\max\left(0,\frac{qk^{(4)^T}}{|q|_2\cdot\left|k^{(4)}\right|_2}\right)}{\sum_{i=1}^N\max\left(0,\frac{qk^{(4)^T}}{|q|_2\cdot\left|k^{(4)}\right|_2}\right)} \\ &h_{\mathrm{att}} =\varphi_{\mathtt{all}}(e)=\sum_{i=1}^Na_{\mathtt{all}}^{(i)}v^{(i)} \end{aligned} $$
若无特殊说明,以上需要生成的变量均服从正态分布
实验分析
数据说明:
- A 股市场除停牌或其他异常股票外的所有股票的日均价量数据
- 采用 Qlib 平台的 Alpha158 数据集,其中包含 158 个技术特征
- 将数据分为训练(3432只股票,从01/01/2010到12/31/2017)、验证(3450只股票,从01/01/2018到12/31/2018)和测试(3923只股票,从01/01/2019 至 12/31/2020)数据集
评价指标:排名信息系数(Rank IC)、Rank ICIR
Rank IC 可用于评估股票的横截面收益,根据预测/真实收益率对股票分别进行排序,再通过 Spearman 秩相关系数度量两种排序结果之间的一致性;Rank IC 值越大,模型效果越好
Rank ICIR 由Rank IC 的平均值除以标准差计算得出
不同模型的性能对比:

- FactorVAE-prior 是本文模型的一个变体,去除了先验-后验学习方法;由此可知,最优后验因子对预测因子的指导,是本文模型预测性能改善的一个重要环节
鲁棒性实验(随机删除 m 只股票并作为额外的测试集)

回测收益曲线(TopK-Drop 策略,保留最好的 50 只股票,每次换掉其中最差的 5 只)

其他回测评价(年化收益 AR、夏普比率 SR 和最大回撤 MDD):

相关资源
- 论文在线地址
- 本地文件地址:Duan et al_2022_FactorVAE.pdf
- 本地Zotero地址:Duan et al_2022_FactorVAE.pdf