1 FTC1的第二形式
$$\Delta F=Ave(F')\Delta x$$
推导过程
- 由FTC1可知$\Delta F=F(b)-F(a)=F\int_a^bf(x)dx$
- 而$\frac{\Delta F}{\Delta x}=\frac{1}{b-a}\int_a^bf(d)dx=Average(F)$,即$\Delta F=Ave(F')\Delta x$
与中值定理的对比
- 中值定理(MVT)描述的是$\Delta F=F'(c)\Delta x$
- 其中$c$并不确定,只是泛指定义域内的某一位置
- MVT只能给出一个范围,即$F'{min}\leq F'(c)\leq F'{max}$
- FTC1给出了一个具体值,即函数$F'$的平均值$Ave(F')$
- FTC1比MVT的效果更强(更具体、更约束)
2 微积分第二基本定理
Fundamental Theorem of Calculus(FCT2): $$\text{已知函数}f(x)\text{连续,定义}G(x)=\int_a^xf(t)dt\text{,则}G'(x)=f(x)$$
证明过程
- 由FTC1可知$\Delta G\approx\Delta x\times f(x)$
- 由此可得$\lim_{\Delta x\to 0}\frac{\Delta G}{\Delta x}=f(x)$,得证
3 微积分基本定理的应用
- ”New“ number,比如对单位圆函数定积分可以得到$\pi$
- "New" function,一个初等函数都可以通过定积分得到一个超越函数
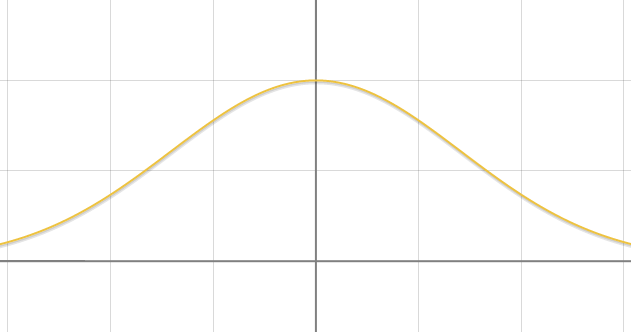
超越函数示例:$F(x)=\int_0^xe^{-t^2}dt$
- 函数$e^{-t^2}$也被称为钟型函数,其函数图像如下:
- 原函数$F(x)$的几何定义为钟型函数曲线下的面积
- 原函数$F(x)$不能用基本函数表示,但可以确定$F(0)=0$
- 函数$e^{-t^2}$可以作为原函数$F(x)$的导数探究原函数的图像性质
- 通过取极限$x\to \infty$,可以得到原函数的两条渐近线:
- $lim_{x\to \infty}F(x)=\frac{\sqrt{\pi}}{2}$ 和 $lim_{x\to -\infty}F(x)=-\frac{\sqrt{\pi}}{2}$
4 参考