1 连续平均
continuous average: $$lim_{n\to \infty}\frac{y_1+y_2+...+y_n}{n}=\frac{1}{b-a}\int_a^bf(x)dx$$
例题1:单位半圆$y=\sqrt{1-x^2}$的平均高度 $$\frac{1}{1-(-1)}\int_{-1}^1\sqrt{1-x^2}dx=\frac{\pi}{4}$$
例题2:以弧长/角度$\theta$为自变量的单位半圆$y=sin(\theta)$的平均高度 $$\frac{1}{\pi}\int_0^{\pi}sin\theta d\theta =\frac{2}{\pi}$$
2 加权平均
weighted average: $$\frac{\int_a^bf(x)w(x)dx}{\int_a^bw(x)dx}$$
- 其中$w(x)$为权重函数
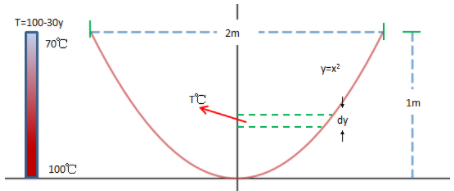
例题1:一个高度1m,锅口直径为2m的坩埚,其形状由函数$y=x^2$围绕$y$轴旋转而成,锅中盛满水后热一段时间后,锅底温度是100℃,水面温度是70℃,现假设温度的函数是T = 100 – 30y,计算整锅水的总热量
- 此例题承接于上一节壳层法的内容
- 明确一个物理计算过程:能量=体积×温度
- 所以$总热量=\int_0^1T(\pi x^2)dy=\int_0^1(100-30y)(\pi x^2)dy=40\pi$
- 注意单位转换,目前的能量单位是摄氏度乘以立方米($deg\times m^3$)
- 而由于$1cal=1deg\times cm^3$,$100cm=1m$
- 因此最终总热量为$40\pi deg\times m^3(\frac{1cal}{1deg\times cm^3})(\frac{100cm}{1m})^3=40\pi \times 1000kcal$
插播一条科普
- 1卡路里表示1千分之一升(即$1cm^3$)水加热1度需要的热量
- 一根棒棒糖的热量约为250卡路里
- 加热上题中的坩埚至煮沸(70~100℃),只需要约500根棒棒糖~
例题2:计算上面那锅水的平均温度
- $T_{平均}=\frac{\int_0^1{T\pi ydy}}{\int_0^1{\pi ydy}}=80℃$
- 权因子是$\pi y$,即$w(y)=\pi y$,最终的平均温度是80℃
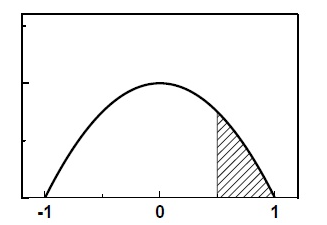
例题3:随机地在区域 $0<y<1-x^2$ 内选取一点,那么$x>\frac{1}{2}$的概率是多少?
- $x$ 的区间限制在$[a,b]$,并且$a\leq x_1<x<x_2\leq b$
- 则此类概率计算的通用公式为$P(x_1<x<x_2)=\frac{\int_{x_1}^{x_2}{w(x)dx}}{\int_a^b{w(x)dx}}$
- 此题最终结果$\frac{\int_{0.5}^{1}{(1-x^2)dx}}{\int_{-1}^1{(1-x^2)dx}}=\frac{5}{32}$
3 参考