1 圆盘法(method of disks)
求半圆函数$(x-a)^2+y^2=a^2$绕$x$轴旋转一周后所形成球的体积$V$
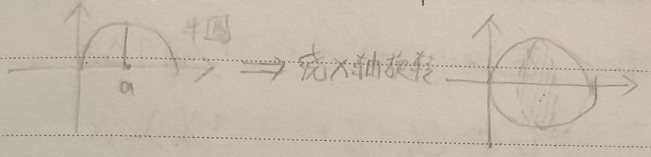
- 半圆函数可化简得$y^2=2ax-x^2$
- 球的每一个切面都是一个圆:$dV=\pi y^2dx$
- 由此可得$V=\int_0^{2a}\pi (2ax-x^2)dx=\frac{4}{3}\pi a^3$
- 球的部分体积满足函数$V(x)=\pi (ax^3-\frac{x^3}{3})$
2 壳层法
求函数$y=x^2(y\leq a)$绕$y$轴旋转一周后所形成的物体体积$V$

- 和圆盘法的思路类似,只不过这次是围绕y轴一圈一圈的表面积累加
- 由$dV=2\pi x(a-x^2)dx$可得$V=\int_0^{\sqrt{a}}2\pi (ax-x^3)dx=\frac{\pi}{2}a^2$
注意点:
- 带入现实问题时,需要注意单位换算的问题
- 以$y=x^2$为例,$y$和$x$其实都是长度单位,而$y=x^2$违背了比例原则
- 此时的单位换算可能存在悖论。具体举例来说,当$y=1m$时,$x=1m$,而当$y=100cm$时,$x=10cm$。
- 实际应用问题中,应该结合实际情况来正确解读变量的单位
3 参考
