1 高级数据类型
1.1 元胞数组
- 以其他数组的副本为元素的多维数组
- 使用
cell函数可以创建空矩阵的元胞数组 - 通过花括号
{}来创建元胞数组更常见 - 元胞数组可用于存储不同大小的矩阵序列
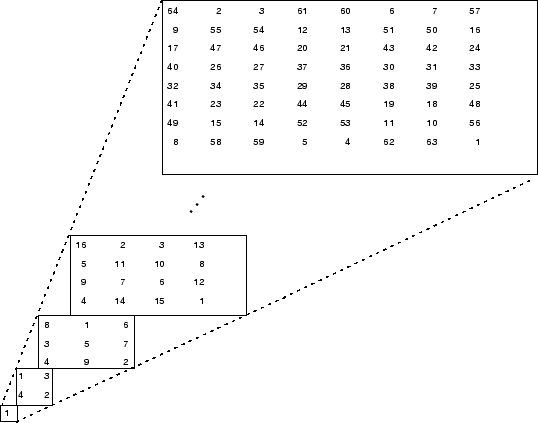
M = cell(8,1);
for n = 1:8
M{n} = magic(n);
end
M
% reuslt
M =
[ 1]
[ 2x2 double]
[ 3x3 double]
[ 4x4 double]
[ 5x5 double]
[ 6x6 double]
[ 7x7 double]
[ 8x8 double]
1.2 结构体
结构体是多维 MATLAB 数组,包含可按文本字段标志符 访问的元素。例如:
S.name = 'Ed Plum';
S.score = 83;
S.grade = 'B+'
与 MATLAB 环境中的所有其他内容一样,结构体也为数组,因此可以插入其他元素。在本示例中,数组的每个元素都是一个具有若干字段的结构体。可以一次添加一个字段:
S(2).name = 'Toni Miller';
S(2).score = 91;
S(2).grade = 'A-';
也可以使用一个语句添加整个元素:
S(3) = struct('name','Jerry Garcia',...
'score',70,'grade','C')
性能提升
1 向量化
很多时候for 循环可以替换为矩阵运算
x = 0.01;
y = log10(x);
for k = 1:999
x(k+1) = x(k) + 0.01;
y(k+1) = log10(x(k+1));
end
以上代码的向量化版本为
x = .01:.01:10;
y = log10(x);
1.1 预分配
通过预分配存储输出结果可以提高 for 循环的运行速度
r = zeros(32,1);
for n = 1:32
r(n) = rank(magic(n));
end
原因分析:在未进行预分配的情况下,向量r将随着循环增加长度,影响程序性能
2 数值分析
2.1 线性代数
z = [1+2i 7-3i 3+4i; 6-2i 9i 4+7i];
z' % z的复共轭转置
z.' % z的非共轭复数转置
eye(2,3) % 返回2×3矩形单位矩阵
A = pascal(3);
inv(A) % 矩阵求逆
det(A) % 行列式
kron(X,I) % Kronecker 张量积
相关参考:Kronecker 乘积
2.2 微积分
差分:
X = [1 1 2 3 5 8 13 21]; Y = diff(X) % result Y = 0 1 1 2 3 5 8
diff(X,n):通过递归应用diff(X)运算符n次来计算第 n 个差分diff(X,n,dim):沿dim指定的维计算的第 n 个差分
向量的梯度
x = 1:10 fx = gradient(x) % result fx = 1 1 1 1 1 1 1 1 1 1
多项式微分
p = [3 0 -2 0 1 5]; % 多项式的向量表示 q = polyder(p) % result q = 15 0 -6 0 1
积分:
fun = @(x,c) 1./(x.^3-2*x-c); % 带参数c的匿名函数 q = integral(@(x) fun(x,5),0,2) % 计算从 `x=0` 至 `x=2` 的积分
integral2(fun,xmin,xmax,ymin,ymax):对二重积分进行数值计算integral3(fun,xmin,xmax,ymin,ymax,zmin,zmax):对三重积分进行数值计算
多项式积分
p = [3 0 -4 10 -25]; q = polyint(p) % 积分后的多项式 a = -1;b = 3; I = diff(polyval(q,[a b])) % 多项式积分值
2.3 数据拟合
曲线拟合也叫曲线逼近,与插值函数有些区别,其只要求拟合的曲线能合理地反映数据的基本趋势,并不要求曲线一定通过数据点。曲线拟合有几种不同的判别准则,如使偏差的绝对值之和最小、使偏差的最大绝对值最小和使偏差的平方和最小(即最小二乘法)。常用的方法是最后一种。
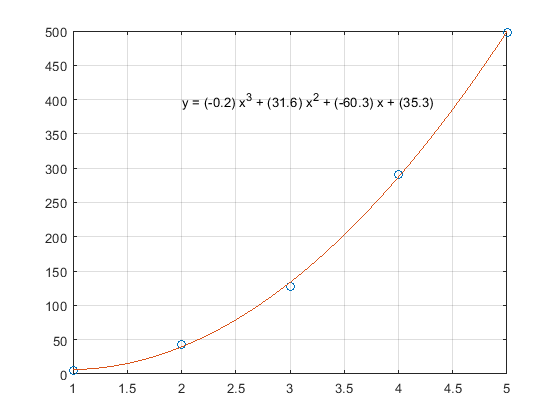
多项式拟合
x = [1 2 3 4 5]; y = [5.5 43.1 128 290.7 498.4]; p = polyfit(x,y,3) % 得到向量表示的拟合多项式 x2 = 1:.1:5; y2 = polyval(p,x2); % 自变量带入多项式并得到因变量 plot(x,y,'o',x2,y2) grid on s = sprintf('y = (%.1f) x^3 + (%.1f) x^2 + (%.1f) x + (%.1f)',p(1),p(2),p(3),p(4)); text(2,400,s)
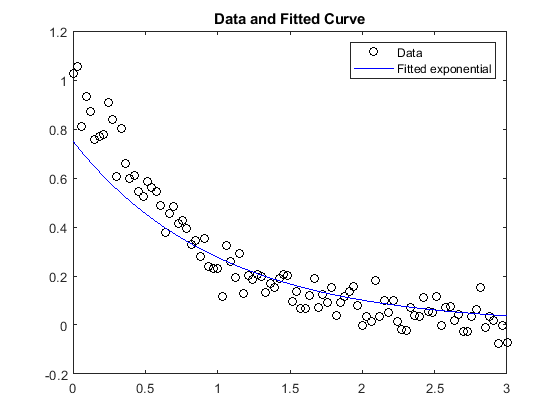
非线性拟合
rng default % for reproducibility xdata = linspace(0,3); ydata = exp(-1.3*xdata) + 0.05*randn(size(xdata)); lb = [0,-2];ub = [3/4,-1]; % 添加函数参数约束 fun = @(x,xdata)x(1)*exp(x(2)*xdata); % 规范拟合函数形式 x0 = [1/2,-2]; % 拟合的初始点 x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub) plot(xdata,ydata,'ko',xdata,fun(x,xdata),'b-') legend('Data','Fitted exponential') title('Data and Fitted Curve')
时间序列拟合
load enso; % 导入数据:厄尔尼诺现象数据 [curve, goodness, output] = fit(month,pressure,'smoothingspline'); % 返回值说明:拟合值;拟合度统计;拟合算法信息 plot(curve,month,pressure); xlabel('Month'); ylabel('Pressure');
拟合模型类型列表
类型简称||类型详情|
|---|---|---|
|'poly1'||Linear polynomial curve 线性多项式曲线|
|'poly11'||Linear polynomial surface 线性多项式曲面|
|'poly2'||Quadratic polynomial curve 二次多项式曲线|
|'linearinterp'||Piecewise linear interpolation 分段线性插值|
|'cubicinterp'||Piecewise cubic interpolation 分段三次线性插值|
|'smoothingspline'||Smoothing spline (curve) 样条平滑曲线|
|'lowess'||Local linear regression (surface) 局部线性回归曲面|
2.4 数值求解
线性方程组
A = magic(3); B = [15; 15; 15]; x = A\B % A\B等效于mldivide(A,B)
非线性方程式
myfun = @(x,c) cos(c*x); % parameterized function c = 2; % parameter fun = @(x) myfun(x,c); % function of x alone x = fzero(fun,0.1) % result x = 3.1416
非线性方程组
F(1) = exp(-exp(-(x(1)+x(2)))) - x(2)*(1+x(1)^2); F(2) = x(1)*cos(x(2)) + x(2)*sin(x(1)) - 0.5; x0 = [0,0]; % 从 0,0处开始求解方程组。 x = fsolve(F,x0) % result x = 0.3532 0.6061
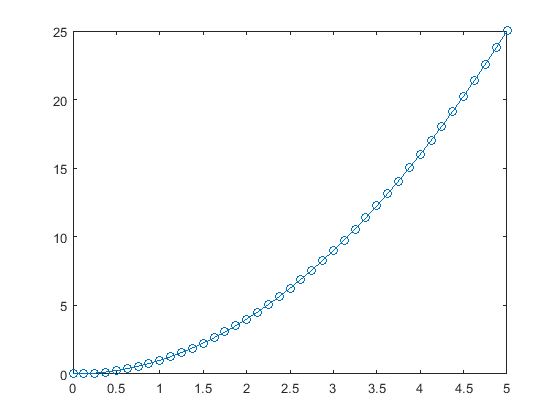
常微分方程式
tspan = [0 5];y0 = 0; [t,y] = ode45(@(t,y) 2*t, tspan, y0); plot(t,y,'-o')
大多数情况下,可以首先尝试求解器 ode45
ode23更适合对误差容忍度更高的情况
ode113更适合对误差容忍度更低的情况