中文标题:众包平台实体解析算法
英文标题:Crowdsourcing algorithms for entity resolution
发布平台:VLDB
Proceedings of the VLDB Endowment
发布日期:2014-08-01
引用量(非实时):208
DOI:10.14778/2732977.2732982
作者:Norases Vesdapunt, Kedar Bellare, Nilesh Dalvi
文章类型:journalArticle
品读时间:2022-01-26 11:05
1 文章萃取
1.1 核心观点
数据库中记录有可能指向不同的重复实体,ER的目标是尽可能消除重复的实体(比如最早的皇帝是指秦始皇,最早统一文字的皇帝是指嬴政,数据库应该理解并建立嬴政与秦始皇是相同实体的关系)。本文先通过机器学习模型的输出概率初步建立实体之间的边,然后通过向人类提出问题的方式验证边,从而实现重复实体的关联。而本文的核心问题是建立最优策略,用最少的提问实现重复实体的关联。本文分析了已有的几种策略,并提出了一种有理论保证的备选策略,并在公共数据集和facebook的生产系中验证了策略的有效性。
1.2 综合评价
- 论证了算法复杂度的最优情况和不同实现方法的理论边界
- 提出了一种实际表现良好、显著降低成本的实体消除重复策略
- 通过多种方式验证了模型的抗干扰能力
- 数学推理过程严谨(略有些枯燥,个人后半部分没硬啃),方法创新性一般
1.3 主观评分:⭐⭐⭐⭐
2 精读笔记
2.1 简介与背景
向人类询问的费用和时间成本都很高,一般来说可以通过平等关系的传递性来减少提问次数。比如说,已知秦始皇是嬴政,秦始皇是最早的皇帝,所以嬴政是最早的皇帝。
本文的目的就是最小成本(最少提问次数)的最大收益(尽可能解决实体的重复关系),同时本文还对最优问题属于NP-hard问题,计算复杂度的边界(最差情况)进行了探究,并提出两种备选策略,与其他策略进行对比与评估,并进行策略的改进。
本文研究主要采用的是facebook的位置数据库,这份数据库有很多用户录入的地理位置信息,由于缩写、拼写问题、标记位置与实际位置误差等问题,导致了大量的位置重复的情况。针对此问题,本文会先通过训练机器学习模型做到初步的重复记录及其置信度的标记。
以实体“斯坦福大学”为例,相关的重复实体如下所示:
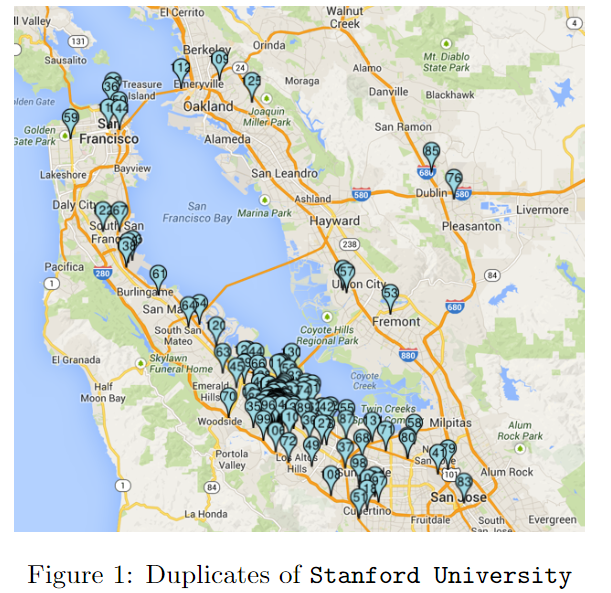
本文的众包平台也是来自facebook的已有工具,支持用户对地理信息的更改和完善。当然和其他众包平台一样,每一份信息的确认会需要来自多个用户的反复认可。众包工具界面示例如下:
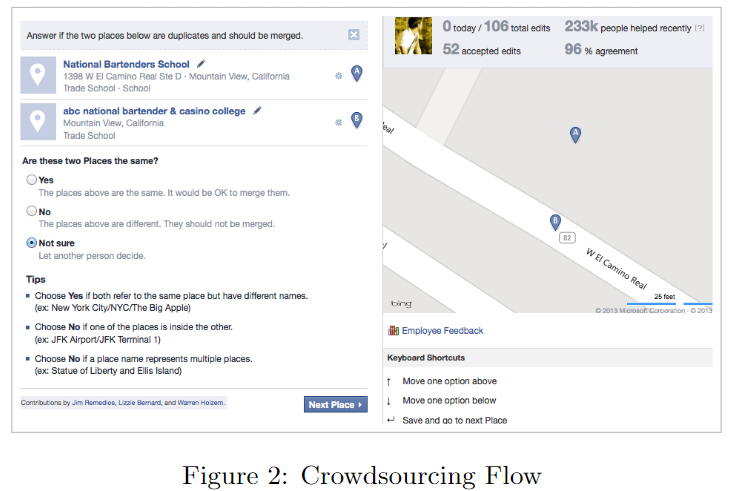
对于ER问题来说,咨询问题的顺序是非常关键的因素,比如判断A, B, C三个实体的关系(先假设A!=B=C),如果先咨询A与B,可知A!=B,再咨询B与C,可知B=C,即可推出A与C的关系,即A!=C。而如果先咨询A与B,得知A!=B,再咨询A与C,得知A!=C,需要继续判断B与C。
本文希望找到最小成本地修正机器学习结果的策略,而策略本质上是一个咨询问题的排序问题。
2.2 符号定义与问题
设$X={x_1,...,x_n}$ 为实体的集合,$G(X,E)$为以$X$元素为顶点构建的无向图
设$p$为分配给每条边$e\in E$的概率$p(x_i,x_j) \in [0,1]$,描述顶点$x_i$和$x_j$间匹配的可信度
比如顶点数为3,并且所有边概率均为0.5的图示例如下:
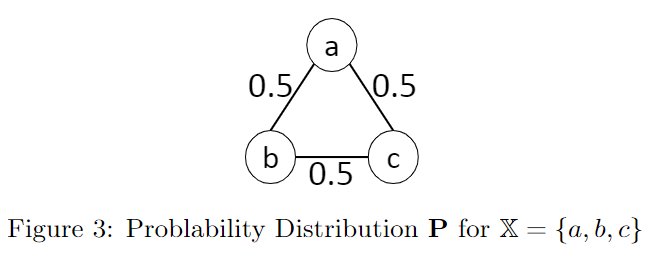
当基于$X$构建的图$C$是传递闭包(transitively close)时,称$C$是$X$的一个集群(clustering)
设$L(G)$表示$G$中所有满足传递闭包的子图集合,即$X$的所有可能集群集合
用$\Delta$表示事件,$Q=P(.|\Delta)$为在$\Delta$条件下的概率分布。简而言之,$Q$描述了$L(G)$的概率分布。
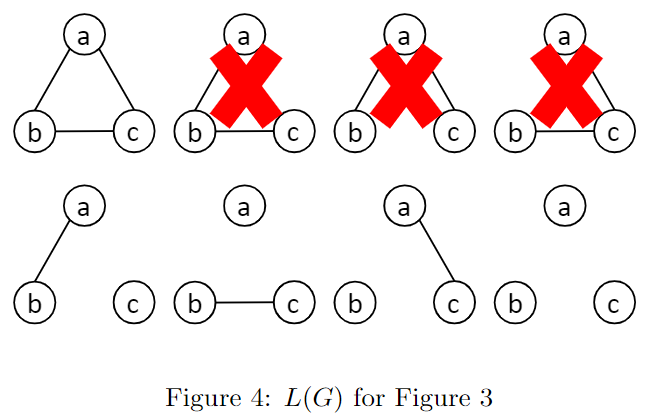
三个顶点所能构建的无向图共有8种,其中满足传递闭包的有5种
假设边的概率均为0.5,则每种集群的概率均等,$Q(C)=0.2$
在本文中,默认人类问答是正确的,实际情况中,会通过多人投票的方式选择最可能的答案
在本文中,默认图$G$是连通的,因为不连通的情况,可以对每一个连通子图进行同样的策略
用$\pi$表示策略,策略用决策树的方式存储,用树的内部节点对应一对实体,根据这一对实体是否存在匹配关系产生两个子节点。最终的叶节点对应了集合$X$的一种可能的集群$C$。构建集群的过程中的咨询次数即策略的成本$cost(\pi)$,而最优策略$\pi_{opt}$的目的就是追求最小成本。
2.3 最优策略复杂度分析
定义$(G(X,E),p)$是问题实例,其中$G$为连通图,图$G$有$|X|=n$个节点
引理 3:设$T=T^+\cup T^-$是一个边的正确结果集。则$T^+$表示答案为$YES$的边集,$T^-$表示答案为$NO$的边集
对于集群$C$来说,内部都可以根据是否连通继续划分为多个簇(cluster),簇用符号$c$表示:
簇$c$内的所有边汇总并用$edges(c)$表示,而$edges(c_1,c_2)$则表示簇$c_1$与簇$c_2$之间的所有可能的边
引理4:对于任意簇$c$,策略$\pi$需要确定$edges(c)$中的$|c|-1$条边(因为最后一条边可以通过前面的$|c|-1$次结果推断出来)
引理5:对于任意的两个簇$c_1,c_2$,策略$\pi$需要至少确定$edges(c_1,c_2)$中的一条边
引理6:对于任意的策略$\pi$和集群$C$,$cost(\pi,C)\leq 2(n+1)cost(\pi_{opt},C)$
证明:
- 按照簇是否单节点对集群$C$进行切分,分为单节点集群$C_1$和多节点集群$C_2$
- 设$|X|=n$,$|C_1|=k_1$,$|C_2|=k_2$,则$C_1$内节点数也为$k_1$(因为一个簇都只有一个节点),而$C_2$内节点数为$n-k_1$,并且$k_2\leq (n-k_1)/2$(因为$C_2$每个簇都至少两个节点)
- 根据引理4可知,所有簇的确定内部边需要次数为$\Sigma_{c\in C}|c|-1=n-|C|=n-k_1-k_2$
- 簇之间的边确定需要分两种情况:1)$C_1$内单节点簇之间 2)其他情况
- 第一种情况,假设对于图$G$,有$l$条边在$C_1$中需要确定,则根据引理5可知,至少需要确认$l$次
- 所以最优策略的下限为$cost(\pi_{opt},C)\geq (n-k_1-k_2)+l\geq (n-k_1)/2+l$
- 而针对第二种情况,主要分为多节点簇之间与多节点簇与单节点簇之间,前者最多需要确定$(n-k_1)(n-k_1)$次,后者最多需要确定$k_1(n-k_1)$次,合并最多需要$n(n-k_1)$次
- 所以普通策略的上限是$cost(\pi)\leq (n-k_1-k_2)+l+n(n-k_1)\leq (n+1)(n-k_1)+l$
- 得证
引理7:对于任意的策略$\pi$,$cost(\pi)\leq 2(n+1)cost(\pi_{opt})$
所以,最优策略的算法复杂度会比普通策略最多低$O(n)$
2.4 已有算法分析与反驳
本小节针对Wang等人的论文中的策略j进行反驳
首先理解提问顺序对于策略的重要性:
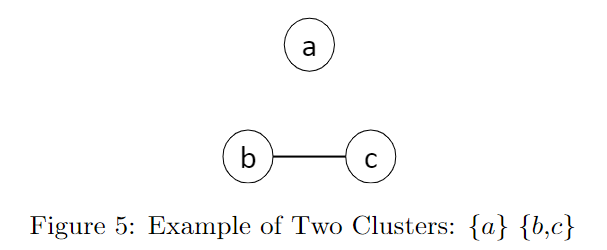
对于$X={a,b,c}$的情况,假设最终的集群$C$包含两个簇${a}$和${b,c}$,则可能有以下两种策略:
- 策略1 - $(a,b),(a,c),(b,c)$,必须要进行三次询问才能得到所有节点之间的关系
- 策略2 - $(b,c),(a,b),(a,c)$,前两步已经可以推断出第三对关系
而Wang等人的论文认为的“最优”策略是$\pi_{dec}$,即以概率$p(e)$递减的顺序进行边的询问策略,但这一策略缺乏严格证明,本小节将说明寻找最优策略为NP-hard问题,并且证明$\pi_{dec}$复杂度差于最优策略,差异下界为$\Omega(n)$,和其他策略不存在明显差异。
由于证明过程较为枯燥,因此笔记中暂略,详细证明请参考原论文的4.2、4.3小节。此处仅通过一个简单例子用于对比概率递减法(Decreasing Edge Probablity Order )和关联聚类法(Correlation Clustering),以简单理解本小节的主旨。
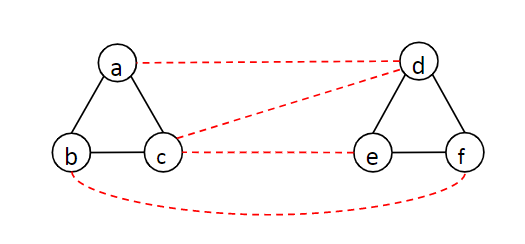
概率递减法示例分析(参考上图):
- 由于边的初始化是基于模型的预测结果,所以存在误差是难免的。本例中,模型预测存在边的情况用虚线/实线表示,其中黑色实线为簇内边,即模型预测正确的情况;红色虚线为簇间边,即模型预测错误的情况。
- 现在假设红色虚线的预测概率大于黑色实线的预测概率,则概率递减法,将会先验证边$(a,d),(c,d),(c,e),(b,f)$的真实值,并得到四个$NO$,之后会验证黑色实现,得到四个$YES$,也就是总共需要验证8次。
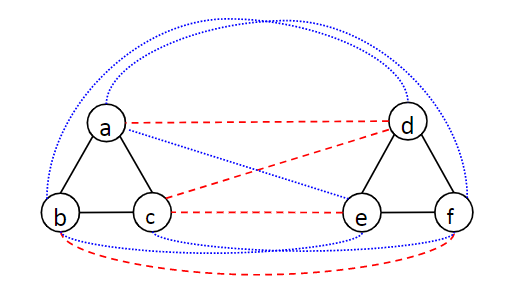
关联聚类法示例分析(参考上图)
- 沿用上例中的情况,并用蓝色虚线表示可能需要验证的负例(模型预测不存在边的情况)
- 关联聚类法通过考虑寻找最小分歧的方式来进行边的验证,比如集群集合${a,b,c}{d,e,f}$如果需要成立,则需要排除掉$(a,d),(c,d),(c,e),(b,f)$边为真的四种情况;而集群集合${a,b,c,d,e,f}$如果需要成立,则需要排除掉$(a,e),(a,f),(c,f),(b,d),(b,e)$ 边为假的五种情况;因此关联聚类法会选择拆分为两个集群而不是合并。
- 之后关联分析法会根据这一结论,先尝试验证集群内的边为真,然后尝试验证集群外的边为假,总共需要验证5次,相比于概率递减法,所需要的验证次数会有显著降低。
2.5 改进算法的提出
首先提出了一个随机查询的方法抛砖引玉:

其中query-cache函数是指查询真实值的过程,即查询多次人工验证得出的结果集
值得一提的是,论文继续证明了(此处笔记暂略,具体详见论文5.1节)随机查询法相比于最优策略的差异上界为$O(k)$,其中$k$表示簇数,一般小于样本量$n$,因此一顿操作猛如虎的概率递减法,似乎还不如随机查询法。
复杂度理论分析往往只关注数量级的变化,而忽略了可能存在的大常数,个人认为在模型预测精度足够的情况下,概率递减法的实际表现可能会存在比随即查询法好的情况,当然此观点仅为脑补,未进行实际验证。
随机查询法具备一个优秀的理论差异上界,但并未充分利用模型的预测信息,基于此本文提出了优先节点法:

优先节点法的思路很简单,选择一个节点$x_i$,然后计算所有已判断节点$X={x_1,...x_{i-1}}$与$x_i$的匹配概率,并根据概率对$X$进行降序重排,并依次进行查询判断,直到找到一条判断成功的边或全部遍历后,再选择下一个节点$x_{i+1}$,并重复以上过程。
优先节点法的计算,其实有点类似于聚类算法中的分配过程,当进行到节点$x_i$,前$i-1$个节点其实已经完成了簇分配的过程,针对节点$x_i$,边的判断成功就是节点完成簇分配,边的判断失败(全部遍历)就意味着节点没有完成簇分配,自建新簇。所以如果最终的簇数未$k$,则每个节点最多只需要判断$k$次,也呼应了随机匹配中的差异上界$O(k)$
2.6 模型实验与评价
实验所用数据集:
| 名字 | 记录数 | 实体数 | 来源 | 数据特征 | 处理方式 | |
|---|---|---|---|---|---|---|
| Cora | 1838 | 190 | 公共数据集 | 标题、作者、会场、日期、页面 | 字符串相似度 | |
| Places | 9000 | 1493 | Facebook数据 | 机器学习模型 | ||
| Product | 1092 | 576 | 公共数据集 | 名字、价格 | [[Jaccard 相似度 | /article/2023/3/21/1774.html]] |
概率递减法(dec)、随机查询法(rand)和优先节点法(node)对比:
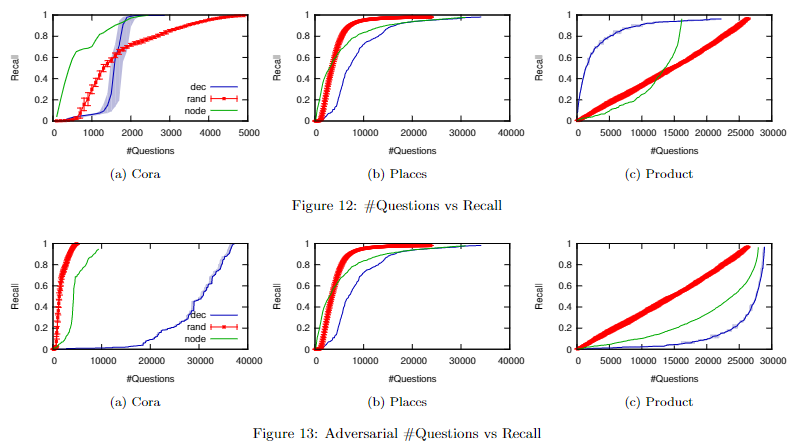
- 其中Figure 12描述的是三种方法最终召回率随着成本(查询次数)增长的变化情况,可以发现不同数据集所适用的最佳方法是不一样的,不存在一招鲜吃遍天的情况
- 对概率进行干扰($p_{new}=1-p_{true}$),模拟模型预测概率很差的情况,可以得到Figure 13中的结果,可以发现此时概率递减法的表现最为糟糕,其次是优先节点法,而没有用到概率信息的随机查询法没有明显变化
为了进一步体现优点节点法的优势,本文又进行了两种概率干扰实验,结果如下:
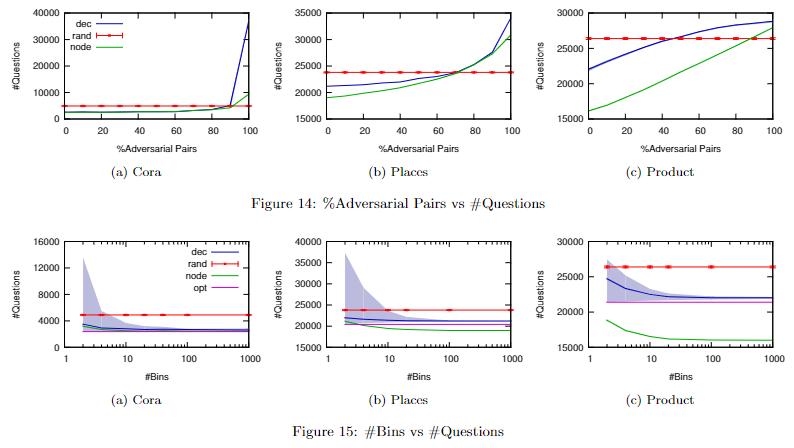
- 其中Figure 14横坐标描述的是概率干扰样本的占比,即$x=20$对应着有百分之二十的样本进行了概率干扰;Figure 15横坐标描述的是对概率进行分桶(bins),即$x=10$对应着将所有可能概率划分到10层桶中,桶内的样本的对比优先级是一致的
- 这两组实验充分体现了优先节点法面对模型预测错误或结果随机扰动情况下的稳健性