中文标题:基于随机图的稳健实体解析
英文标题:Robust Entity Resolution using Random Graphs
发布平台:ACM SIGMOD
Proceedings of the 2018 International Conference on Management of Data
发布日期:2018-05-27
引用量(非实时):22
DOI:10.1145/3183713.3183755
作者:Sainyam Galhotra, Donatella Firmani, Barna Saha, Divesh Srivastava
文章类型:conferencePaper
品读时间:2022-02-15 14:23
1 文章萃取
1.1 核心观点
实体解析主要用于发现并合并重复的实体,本文主要分享了一个通用的纠错工具,用于对存在噪声的算法和数据集进行修正,并提出基于扩展图的查询控制,通过在多个数据集进行实践比较,论证了算法的性能与稳健性。
1.2 综合评价
- 提出随机扩展法对图进行优化,即簇的再合并与再分割
- 基于Extender Pipeline的算法流程优化,在准确度、成本之间取得平衡
- 针对不同数据集和多种算法进行比较,论证丰富可靠
1.3 主观评分:⭐⭐⭐⭐
2 精读笔记
2.1 背景介绍
首先举一个需要实体解析的图片相关示例1:
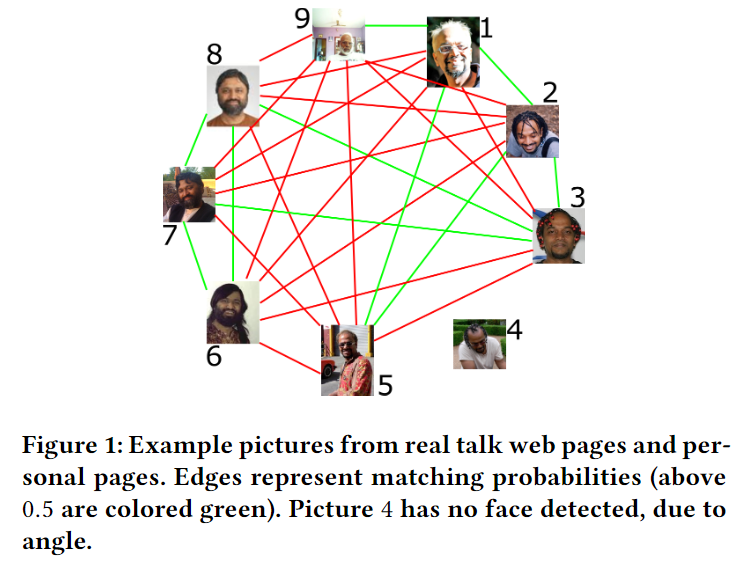
说明:上图中的头像搜集自网络,并通过微软开源工具TwinsOrNot进行面部匹配,绿线表示预测概率大于0.5的情况,红线表示预测概率小于或等于0.5,另外那个孤零零的实体4为未检测到头像的图片。
通常情况下,用Oracle表示实体的真实关联情况,实际应用中可能是通过多次人类验证所得,而示例1的真实情况是,节点1-5是同一个人(S.Muthu,简称SM1),节点6-8是同一个人(Divesh Srivastava,简称DS),节点9是另一个也叫S.Muthu的人,简称SM2,而且SM2长得还挺像SM1。
实体对应的文本类数据示例如下:

说明:实际应用时,文本之间的相似度主要通过Dandelion API获得。虽然SM1和SM2长得很像,并且名字也一样,但是可以根据文本类数据区分出二者的差异,一个喜欢数据算法;一个喜欢人文哲学(文艺算法爱好者:???)
值得注意的是,模型得到的结果是存在错误甚至互相矛盾的,因此需要通过实体解析的方式进行纠错,比如常见的随机查询法和概率递减法(按照概率从高到低排序依次进行边的验证),此类方法都是默认Oracle是完全正确的,并将其返回的结果作为真实值用于纠错。
但是现实中的oracle却不一定完全是正确的,基于此,本文提出了一种通用的纠错层,用于减轻现实oracle中存在的噪声影响。
2.2 算法细节
2.2.1 符号定义
用$V={v_1,...,v_n}$表示样本集,实体解析的目的是探究$v_i$和$v_j$是否指向同一个实体
用$H=(V,A,p_m)$表示图,其中$A\subseteq V \times V$表示图中可能的边,$p_m$表示边的存在概率(匹配的可能性),现实情况中边应该是稀疏的,所以$|A|<<{n \choose 2}$
用$C=(V,E^+)$表示图的真实解,而实际情况下能得到的其实是有噪声的$C'$,即”noisy oracle“
用$q(u,v)=(a,e)$表示样本$u$和$v$指向同一个实体的结果为$a$的错误率为$e$,其中$a\in {YES,NO}$并且$e\in [0,0.5]$。举例来说:$q(u,v)=(YES,0.15)$表示二者指向同一个实体的可能性为0.85,$q(u,v)=(NO,0.21)$表示二者指向同一个实体的可能性为0.21
所有回答为YES的$query$构成了子图$Q_+$,所有回答为NO的$query$构成了子图$Q_-$,$Q=Q_+\cup Q_-$
错误概率$p_e$描述了noisy oracle中的噪音程度,$p_e=0$时,”noisy oracle“就变成了"perfect oracle"
$c'(u)$表示有噪音的情况下,样本$u$所属的簇(内部互相关联的子图),$c'(u)\in C'$,此时$Q_-$与$c'(u)$的交集不为空,这里的交集被称为$Q_-[c'(u)]$
扩展图(Expander graph)是一种具有强连通性质的稀疏图,非常契合理想情况下的Oracle。而本文将提出一种随机扩展法,尝试修正簇间的关联性(簇的再合并与再分割)
2.2.2 随机扩展法
随机扩展法主要通过尝试合并簇或分割簇,对最终的簇分布进行调整和修正,作为最终结果的修正方法,具备一定的普遍适用性。

算法1主要用于判断两个簇是否需要合并。
- 其中$S$包含两个簇间的所有可能边,算法先根据已知的$Q_+$,找到$S$所有已经判断为$YES$的边,并将这些边对应的错误概率$p_e$相乘,实现簇间联合错误率$p$的初始化
- 之后随机遍历所有剩余的可能边(不包含在$Q$内的边),计算对应错误概率,如果$Q$中存在不匹配的概率大于0.95的情况,则直接返回false,即一票否则两个簇合并的可能
- 否则对$p$进行乘法累积更新,当更新后的簇间联合错误率小于指定阈值(经验公式:$1/(e(|c_x|+|c_y|))^{\beta(min(|c_x|+|c_y|))}$)时,返回true,即判定两个簇是可以合并的
- 遍历结束时,则根据$S$是否都为判断为$YES$的边来决定是否合并两个簇
- 此算法存在超参$\beta$用于调整簇间联合错误率的判断阈值,取值越小最终图越稀疏,查询成本越低,取值越大,最终图约稠密,精确度越高
需要注意的是,为了保证修正的公平性和准确度,
query_multiple_edges函数中的概率计算方法应该独立于查询结果集$Q$

算法2主要用于遍历所有可能需要合并(line1~lin9)、分割(line10~line16)的簇,然后交给query_multiple_edges函数判断。
- 其中
next_edge_cbn函数会返回可能需要合并的两个簇,输出顺序主要根据簇间累加匹配率(具体计算公式为$cbn(c_i,c_j)=\Sigma_{u,v\in c_i\times c_j}p_m(u,v)$)进行降序排列所得 - 其中
next_node_cp函数会返回可能需要分割的簇,输出顺序主要依据簇内累积错误率(具体公式为$cp(c)=\Pi_{u,v\in c,(u,v)\in Q_+}P_e(u,v)$)进行降序排列所得 - 此算法存在超参$\tau$用于限制簇间合并判断的循环次数,在本文中其默认值为$log(n)$
本文中对于扩展图的“拓展性”量化主要通过边拓展性实现,而经过随机扩展法处理后的图,其边拓展性将有较大的概率接近1。具体证明过程详见论文4.1小节后半部分和附录C。
2.2.3 算法流程优化
随机拓展法,虽然客观上修正改善了最终的结果,但却容易导致$F$值的降低(随机扩展法在尝试合并两个簇时,不可避免的会将簇间少部分查询结果为$NO$的边修正为$YES$)。为了改善这种情况的出现,本小节提出了三种 Extender Piplines 用于优化算法流程:
- Lazy pipline:仅在最后使用随机拓展法进行修正,最终准确度降低,$F$值变高
- Eager pipline:每一次查询,都使用随机拓展法中的
query_multiple_edges函数判断是否合并和两个簇,并在最终调用随机拓展法。此做法会降低效率,$F$值降低,但是准确度会变高 - Adaptive pipeline:高概率的节点不使用随机拓展法中的
query_multiple_edges函数判断,而是采用普通的判断函数query_edges,综合了前两者的优点,最终表现最好。
2.3 实验评价
所用数据如下:
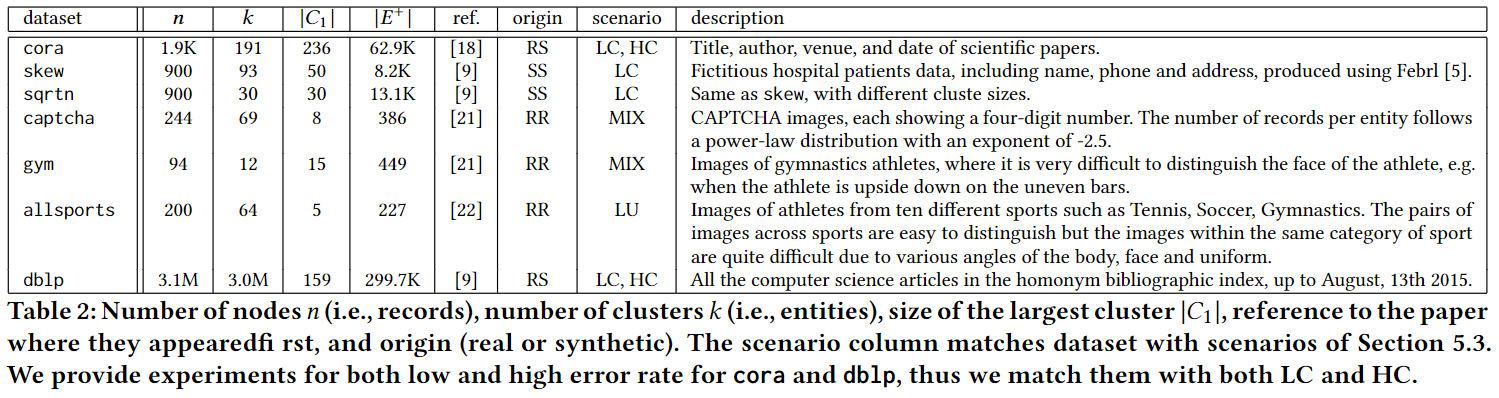
其中$n$表示数据集大小;$k$表示簇的个数;$|C_1|$表示最大簇的大小;$|E^+|$表示边的个数
数据参考文献详见论文;origin列表示属性的真实性和oracle的真实性,其中$R$表示是真实的,$S$表示是带噪音的;scenario列表示算法结果的可靠性和实际应用的可靠性,其中$L$和$H$分别表示算法错误率低和算法错误率高的两种情况,$C$和$U$分别表示结果与实际情况匹配与不匹配的两种情况,$MIX$表示算法错误率适中,并且匹配存在一定噪声的情况。
其他用于对比的算法:
- $dense()$:一种基于高概率算法结果和oracle结果的聚类算法,最终$F$值一般较高
- $vote()$:投票法,出现多种结果时,选择出现次数最多的那种
- $ideal()$:理想模型,理论的模型表现上限
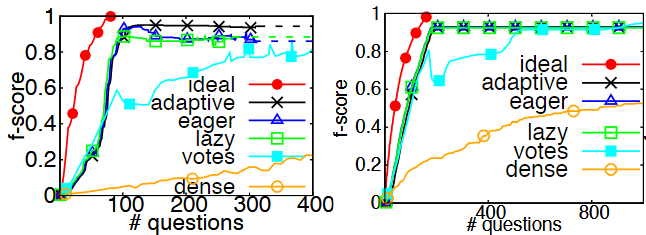
在$RR$类数据集上的表现:
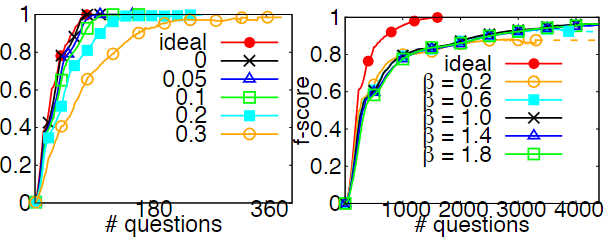
在$RS$或$SS$类数据集上的表现(其中$p^+$和$p^-$分别表示算法预测为$YES$和$NO$的错误率):
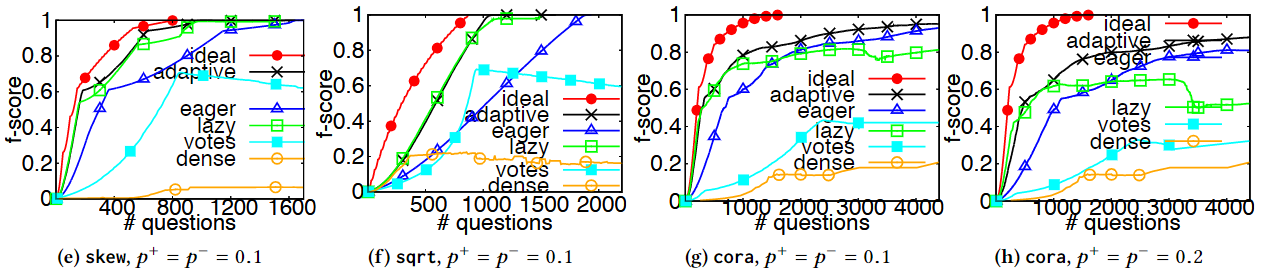
综合以上可以发现,$adaptive$方法取得了仅次于理想模型的最优表现,$lazy$方法在无噪声的数据集上表现优秀,但是随着噪声的增加,性能表现逐渐与$eager$方法拉开距离。
最后再看一下不同错误率水平和超参$\beta$取值对于$adaptive$方法的影响: