上下文无关文法(context-free grammar,CFG):
- CFG 是一种形式语言的描述方式,用于描述一类语言结构,其中语言中的句子可以被分解为符号串,这些符号串是由一组规则递归定义的
- 上下文无关文法重要的原因在于它们拥有足够强的表达力来表示大多数程序设计语言的语法;实际上,几乎所有程序设计语言都是通过上下文无关文法来定义的。
- 另一方面,上下文无关文法又足够简单,使得我们可以构造有效的分析算法来检验一个给定字符串是否是由某个上下文无关文法产生的
CFG的形式化定义可以表示为一个四元组 $G=(V,T,P,S)$
- 其中 $V$ 是非终结符号(即可以继续分解的符号)的集合,$T$ 是终结符号的集合,$P$ 是产生式规则的集合,$S$ 是起始符号(特殊的非终结符号,表示整个语言的起点)
- 产生式规则的形式可以表示为 $A \rightarrow \alpha$,其中 $A\in V$,$\alpha \in (V \cup T)$,即由非终结符号和/或终结符号组成的任意符号串。上下文无关文法取名为“上下文无关”的原因就是因为字符 $A$ 总可以被字符串 $\alpha$ 自由替换,而无需考虑字符 $A$ 出现的上下文
- 如果一个形式语言是由上下文无关文法生成的,那么可以说这个形式语言是上下文无关的。(条目上下文无关语言)
在 CFG 中,每个规则有一个左部和一个右部:
- 左部是一个非终结符号,右部则是由终结符号和/或非终结符号组成的串。通过递归地应用这些规则,可以生成出符合该 CFG 定义的语言中的所有句子。
- 一个被 CFG 所定义的符号串 $w \in (V \cup T)$ 可以被分解为一系列的产生式规则,使得每个产生式规则中的非终结符号都可以被替换为相应的右部符号
一个例子:约束日期类的文法
合法的:2021 年 2 月 1 日;1995 年 10 月 31 日
非法的:20211 年 2 月 1 日; 2021 月 2 月 1 日; 2021 年 22 月 1 日
S->Y M D #year month day
Y->YN YT #YN:year number;YT:year tag
YT->"年"
M->MN MT #MN:month number; MT:month tag
MN-> DOZEN #1 到12
MT->"月"
DT->"日"
YN->DIG1_9 DIG0_9 DIG0_9 DIG0_9 # DIG1_9:digit 1 to 9
DIG0_9->ZERO | DIG1_9
DIG1_9->ONE | DIG2_9
DIG2_9->TWO | DIG3_9
DIG3_9-> THREE | DIG4_9
DIG4_9->"4" | "5" |"6" |"7" |"8" | "9"
ZERO->"0"
ONE->"1"
TWO->"2"
THREE->"3"
DOZEN ->DIG1_9 | ZERO DIG1_9 | ONE ZERO | ONE ONE | ONE TWO
D->DN DT
DN-> DIG1_9 | ZERO DIG1_9 | ONE DIG1_9 | TWO DIG1_9 | THREE ZERO | THREE ONE
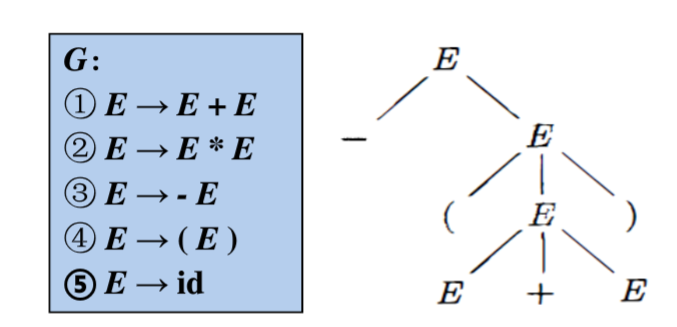
除此之外,CFG 还能以分析树的形式展现: