1 内生性问题
对于回归方程$Y = a + bX + e$,当解释变量$X$和误差项$e$存在相关性时,说明回归模型存在内生性问题
内生性问题的产生原因:
- 遗漏变量(比如在分析学历和收入的关系时,容易忽略个人能力的影响)
- 反向因果(比如分析政策对经济影响时,要意识到经济对政策也是有影响的)
- 选择偏误(样本选择偏误和自选择偏误)、以及测量误差等
内生性问题的后果:在小样本下,内生变量和外生变量估计系数都有偏。在大样本下,内生变量估计系数不一致。外生变量如果与内生变量不相关,则估计系数一致;如果与内生变量相关,则估计系数也不一致
内生性问题的常见处理方法:自然实验法,双重差分法(DID),工具变量法
解决内生性问题关键在于剔除解释变量 $X$ 和误差项 $e$ 之间的相关性
2 自然实验法
自然实验(natural experiment)需要寻找一个事件,并且这个事件只影响解释变量而不影响被解释变量。由此研究对象就会被随机(严格意义上说,事件并不能实现完全的随机)分成了实验组或控制组。
以一篇分析外国博士在美国参与博士后研究的论文为例进行说明:
- 此篇论文在分析美国的博士后劳动力市场后,认为外国博士赴美参与博士后研究(工资较低)有两种常见原因:1. 特别喜欢并热衷于科研而不计较低廉的工资 2. 博士后研究工作能够得到在美国合法居住的身份
- 为了从实证角度验证这两种情况的哪个更常见,此篇论文以92年颁布的一项法案作为分析切入点,该法案对于所有在1990 年4月11日之前抵达美国的中华人民共和国的居民全部授予永久居留权(绿卡)
- 结论:中国赴美读博的人群中会有57%选择继续申请博士后。但是如果博士毕业就能拿绿卡,那么申请的概率就下降到43%。 换句话说,在美国申请博后的中国人中,其中有四分之一是以获取绿卡为目的。
进阶阅读可参阅1_study/CausalInference/随机实验和知乎-自然实验示例
3 双重差分法 DID
双重差分法(Difference-in-Difference ,DID)常用于描述某一次外部冲击的净效应;DID 法一般将受冲击的样本作为实验组,再按照一定标准筛选未受冲击的样本作为对照组,通过两组数据结果做差来评估冲击的净效应
以分析”学区房因素与房价关系“为例,说明 DID 方法:
- 假设某地区之前不存在学区房,然后现在新建了一所著名小学的分校
- 在这一地区内,普通区域 $A$ 转变为学区房,其在建校前后对应的房价波动为 $d_A$
- 由于离得比较远,普通区域 $B$ 在建校后依然不是学区房,其在建校前后对应的房价波动为 $d_B$
- 定义两个区域的房价波动的差异 $d=d_A-d_B$,$d$ 描述了建校事件对房价的冲击
- 最终关于房价 $P$ 的 DID 回归建模方程可描述如下:
$$P=b_0+b_1D_a+b_2D_t+d(D_a\times D_t)+Xb+e$$
- 其中 $b$ 表示回归系数,$D_a$ 为虚拟变量,属于区域 $A$ 时为 1,否则为 0;
- $D_t$ 属于时间虚拟变量,建校后为 1,建校前为 0;时间因素用于描述房价的趋势
- $X$ 表示其他因素,控制住 $X$ 后,$D_a\times D_t$ 描述的便是建校带来的房价提升效应
进阶方法:1_study/CausalInference/因果效应评估_准实验#合成控制法、1_study/CausalInference/因果效应评估算法/双向固定效应 TWFE
4 工具变量法 IV
工具变量(instrumental variable,IV)法是最常见的一种处理内生性问题的方法,其基本思路是:引入和内生变量高度相关的工具变量来替代内生变量,借此剔除原模型误差项和内生变量相关的因素
工具变量需要满足两个基本假设:
- 工具变量外生性,或称为排他性约束(Exclusion Restrictions)。表示工具变量不与其它影响被解释变量的无法观测因素相关,并且工具变量只能通过影响内生变量而影响被解释变量;
- 工具变量相关性(Relevance Condition)。工具变量与内生变量高度相关。
在使用工具变量解决内生性问题前,需要先进行工具变量检验,具体包括外生性检验、相关性检验、以及内生性检验
关于工具变量的构建思路及其示例可参阅知乎-高效的寻找工具变量
两阶段最小二乘(2SLS)是一种用于结构方程分析的统计技术,也是最小二乘法(OLS)法的扩展。IV法可以视为2SLS的特例:当内生变量个数=工具变量个数时,称为IV法;当内生变量个数<工具变量个数时,称为2SLS
假设$y=b_0+b_1x_1+b_2x_2+c$,其中$x_1$是严格外生的,$x_2$是内生的;工具变量为$z$
两阶段最小二乘(2SLS)回归的实现(主要包括两个阶段)
- 第一阶段是借助工具变量$z$把$x_2$分为两部分(与$z$有关/外生部分,与$z$无关/内生部分):
$$x_2=a_0+a_1z+a_2x_2+e$$
- 第二阶段是用$x_2$的拟合值$a_0+a_1z+a_2x_2$代替真的$x_2$去进行回归,得到消除内生性问题的一致评估
工具变量法简单示例:
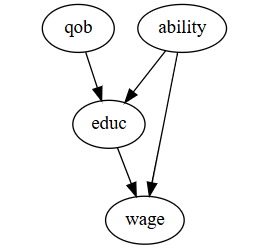
- 实验目的:评估教育(educ)对工资(wage)的影响
- 设计工具变量:美国义务教育法规定孩子必须在入学当年的1月1日之前年满6周岁,并且学生必须上学到16岁才可以合法辍学;因此下半年出生的人平均受教育时长比上半年出生的人更长;所以出生季度(qob)可以是教育时长的工具变量
- 评估工具变量,一个合理的工具变量 $Z$ 需要具备两个条件(1)$Z$ 与干预 $T$ 有关:$\mathrm{Cov}(Z, T) \neq 0$(2)$Z$ 仅通过干预 $T$ 来影响结果 $Y$:$Y \perp Z | T$
- 2SLS 第一阶段回归建模:用工具变量(qob)和协变量 $X$ 预测教育(educ)
$$ \hat{educ}=AX+\alpha \times qob+v $$
- 2SLS 第一阶段回归建模:用教育(educ)拟合值和协变量 $X$ 预测工资(wage)
$$ wage=BX+\beta \times educ+u \approx BX+\beta \times (AX+\alpha \times qob+v)+u $$
- 最后得到 $\beta$ 的回归系数值为 $0.085$,95%置信区间(CI)为 $[0.035,0.135]$;平均而言,每增加一年的教育,工资预计会增长 8.5%
实际建模时推荐使用 linearmodels 包的 IV2SLS 函数
工具变量法的局限性:
- 如何设计并验证一个合理的工具变量,是该方法实践的一大难点
- 2SLS 只是间接评估,因此回归结果置信区间一般比普通线性回归要更宽松
5 其他方法
1_study/CausalInference/因果推断入门#因果效应评估算法分类
1_study/CausalInference/因果效应评估_配平法
1_study/CausalInference/因果效应评估_准实验
1_study/CausalInference/因果效应评估_元学习
Heckman 选择模型、Treatment Effect 模型、RK 拐点回归、结构方程模型等