本小节的示例均围绕以下知识图展开：
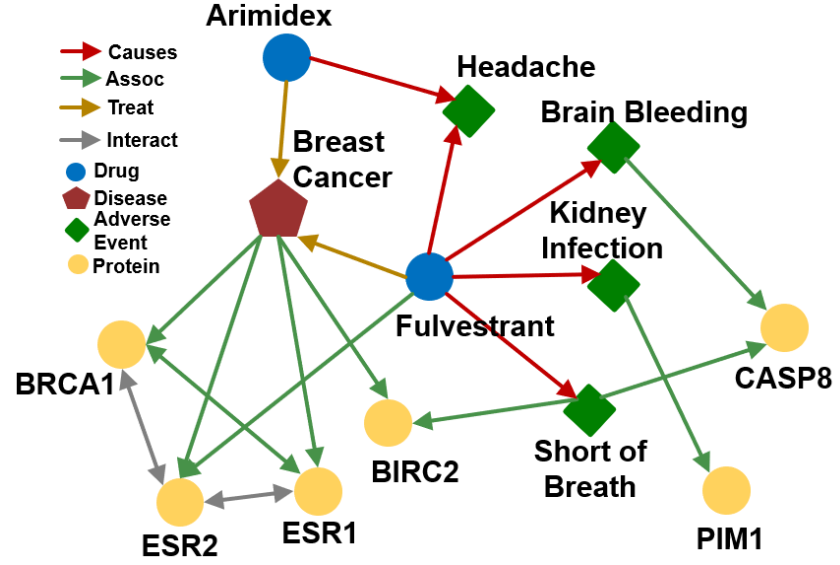
- 该示例数据描述了疾病、药物、不良事件和蛋白质之间的相互关系
1 推理的类型
常见的三种知识图推理类型：
- 单跳查询（one-hop queries），从起始节点经过一条边是否可以达到终止节点，即预测两个节点之间是否有边连接（示例：Fluvestrant 这种药物可能导致哪些不良反应？）
- 路径查询（path queries），从起始节点经过 n 条边是否可以达到终止节点，即预测两个节点之间是否存在可达的路径（示例：哪种蛋白质与 Fluvestrant 引起的不良反应有关？）
- 联合查询（conjunctive queries），从多个起始节点出发，根据关系推理后得到满足条件的终止节点，最后取交集（示例：哪种药物能够治疗乳腺癌但可能引起头痛？）
单跳查询最简单（只是一个最基础的边预测模型），因此不再赘述
路径查询是一个由多次单跳查询组成的链式过程：
- 先从
Fluvestrant节点出发，找到边关系为Causes的不良事件节点集合 - 然后再以每个不良事件节点为起点，找到边关系为
Assoc的蛋白质节点集合
路径查询是对图的遍历，其问题在于实体间的关系可能是不完整或缺失的；对整个图进行需要高额的时间成本，因此一个合理的方式是隐式地估计并解释不完整的知识图（即边预测任务的泛化）
2 知识图的路径查询
核心思想：
- 将路径查询映射到空间中，得到路径查询的向量表示
- 最终目标是追求查询嵌入尽可能地接近答案嵌入
给定路径查询 $q=v_a,(r_1,...r_n)$，其中 $q$ 表示起始节点，$(r_1,...r_n)$ 表示 $n$ 个边条件
借助 TransE 等算法可以实现查询的嵌入表示：$q=v_a+r_1+...+r_n$
路径查询的嵌入表示，就是其实节点的嵌入表示加上多个边的嵌入表示
示例 1：哪些蛋白质与 Fluvestrant 引起的不良反应有关？
示例 1 的路径查询： $v_{Fluvestrant},(r_{Causes},r_{Assoc})$
示例 1 的路径查询可视化：
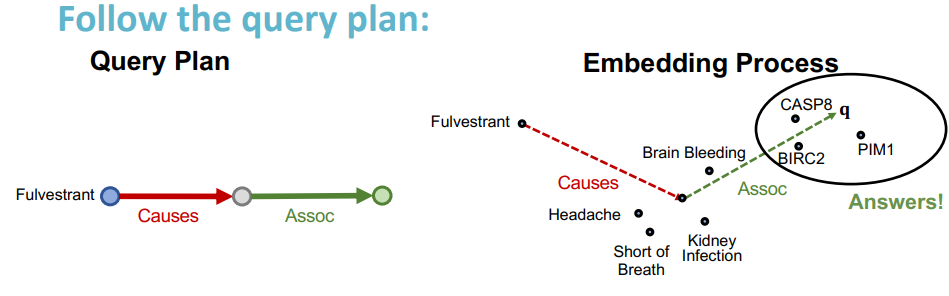
TransR/DistMult/ComplEx 不能处理多个关系的组合，所以不适用于路径查询
3 联合查询的基本概念
联合查询：结合逻辑运算来回答更复杂的查询
联合查询示例 2：有哪些药物能治疗与蛋白质 ESR2 相关的疾病，但会导致呼吸急促？
示例 2 的公式化表示：$((e:ESR2, (r:Assoc, r:TreatedBy)), (e:Short of Breath, (r:CausedBy))$
示例 2 的可视化表示：
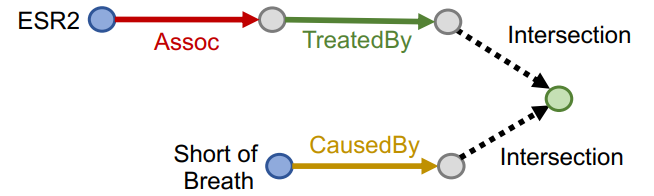
示例 2 的查询过程：
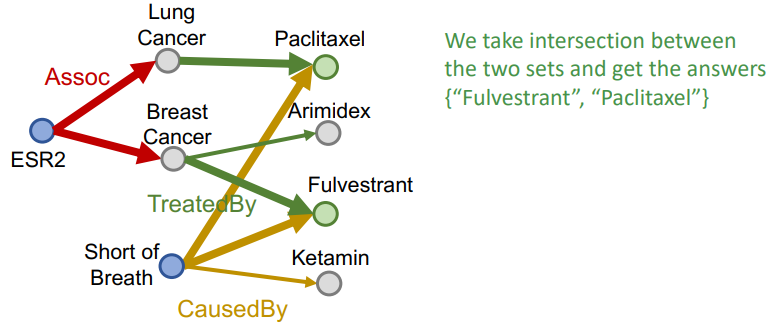（1）先查询和 ESR2 相关（Assoc）的疾病得到：(LungCancer,BreastCancer)
（2）两种疾病根据 TreatedBy 关系查询得到三种药物：(Paclitaxel,Arimidex,Fulvestrant)
（3）根据 CauseBy 关系查询可能导致 ShortofBreath 的三种药物：(Paclitaxel,Fulvestrant,Ketamin)
（4）对步骤（2）和步骤（3）得到的结果取交集，得出最终的答案：(Paclitaxel,Fulvestrant)
问题 1：知识图的边缺失会导致结果失真，如何使用嵌入来隐式插补缺失？
问题 2：如何表示一组实体？如何定义嵌入空间中的交集操作？
4 Query2box 联合查询
Query2box 核心思想：把序列映射成 boxes，每个实体（节点）都是一个包含中心点和偏移项的 box；关系（边）则是一种投影运算；一个 box 可以通过投影运算得到一个新的 box
box 是一个类似超矩阵（hyper-rectangles）的抽象概念，比如查询“药物 Fulvestrant 的所有可能不良事件”可以被包括在一个 box 中，该 box 在嵌入空间中的可视化如下：
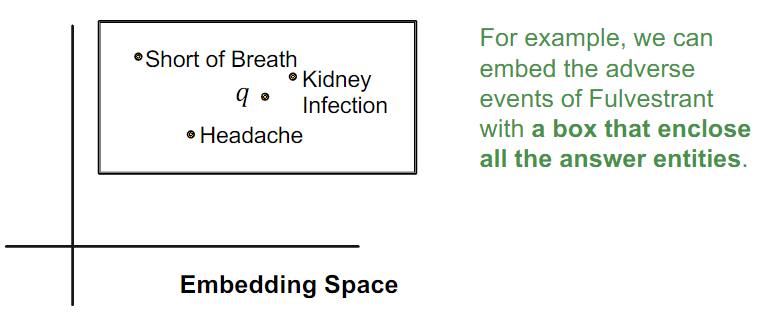
上图可以看出，box 由中心点 $Cen(q)$ 和偏移项 $Off(r)$ 组成
Box 的概念引入，可以很方便的处理嵌入空间中的交集操作
而第三小节中的联合查询示例 2，通过 Query2box 的方式可表示如下：
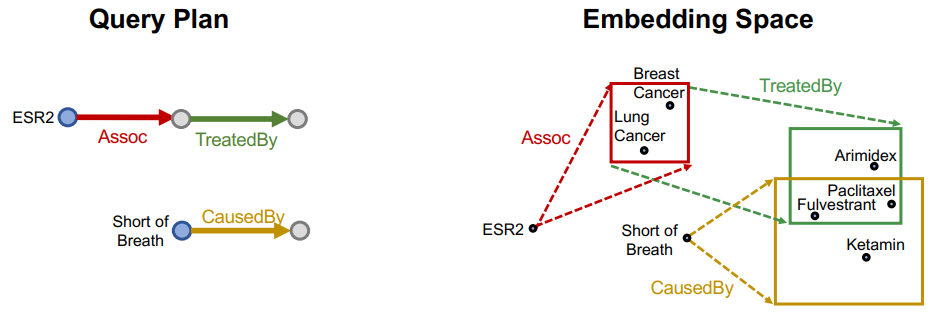
上图可以看出，关系（边）作为一种投影运算，对 box 进行平移和缩放操作
5 联合查询中的交集操作
交集（intersection）操作：将多个 boxes 作为输入并生成交集 box
交集操作的中心点计算： $$ Cen(q_{inter})=\sum\boldsymbol{w}_i\odot Cen(q_i) \\$$
$$ $$ \boldsymbol{w}i=\frac{\exp(f\{cen}^i(Cen(q_i)))}{\sum_j\exp(f_{cen}(Cen(q_j)))}\quad\begin{array}{c}Cen(q_i)\in\mathbb{R}^d\\boldsymbol{w}_i\in\mathbb{R}^d\end{array} $$
- 最终交集输出 box 的中心点是多个 boxes 的中心点的加权均值
- 权重 $w_i$ 则来自神经网络 $f_{cen}$ 训练输出的注意力得分
交集操作的偏移项计算： $$ Off(q_{inter})=min(Off(q_1),...,Off(q_n))\odot \sigma(f_{off}(Off(q_1),...,Off(q_n))) $$
- 最终交集输出 box 的偏移项会小于所有输入 box 的偏移项
- 每个输入 box 的收缩取决于神经网络 $f_{off}$ 输出+ $sigmoid$ 映射
如何定义实体（节点）与 box 之间的距离？
- 距离定义方式 1：实体到 box 中心的距离
- 距离定义方式 2：实体到 box 边缘的距离
- 其他注意：当实体在 box 内部时，距离值为负数
6 联合查询中的并集操作
AND-OR 查询：包含并集操作的联合查询，也称为 EPFO 查询
AND-OR 查询示例："什么药物能治疗乳腺癌或肺癌"
AND-OR 查询的问题：在二维空间中，无法实现基于 box 的并集操作
解决方案：把 AND-OR 查询转化为等效的 DNF（Disjunctive Normal Form，析取范式），即对操作逻辑进行调整和拆分，确保并集操作只在最后一步发生。示例：
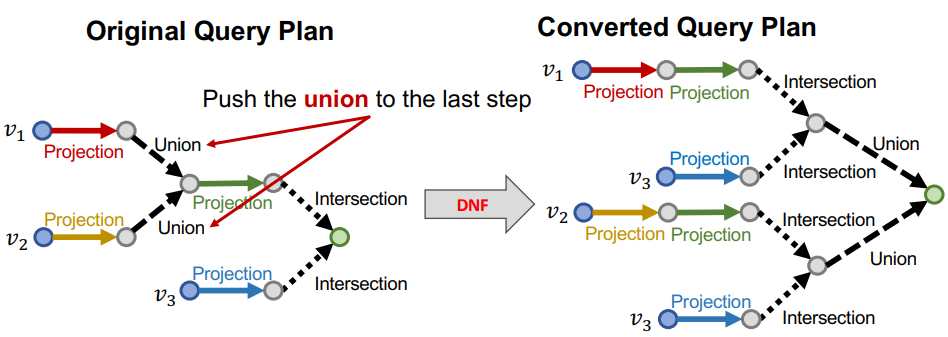
如何定义实体（节点）与多个 box 并集结果之间的距离？
- 假设 m 个 box 的并集结果为 $q=q_1 \cup q_2 \cup ...\cup q_m$
- 实体与 $q$ 之间的距离为 $d_{box}(q,v) = min(d_{box}(q_1,v),...,d_{box}(q_m,v))$
7 Query2box 的训练
Query2box 的训练目标： （1）追求正确实体与最终的 box 之间的距离最小 （2）追求错误实体与最终的 box 之间的距离最大
Query2box 的可训练参数：实体和边的嵌入表示，交集操作涉及的参数
Query2box 的训练过程：
- 在训练图中对查询进行采样，得到答案集合 $v$ 和非答案集合 $v'$
- 根据实体和边的嵌入表示，以及运算符操作，得到查询的嵌入表示 $q$
- 根据答案集合和非答案集合分别计算分数 $f_q(v)$ 和 $f_q(v')$
- 迭代优化可训练参数并追求损失函数 $l$ 最小： $$l=-log\sigma(f_q(v))-log(1-\sigma(f_q(v)))$$
分数 $f_q(v)$ 度量的是节点 $q$ 与集合 v 构成的 box 之间距离的负数）
如何生成复杂的查询？使用查询模板（Query Template）
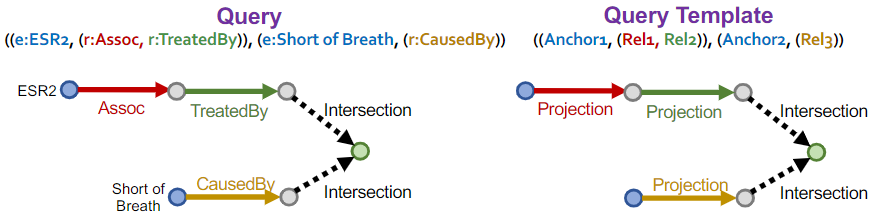
- 先对模板中答案相关的节点进行实例化，然后随机采样一个答案节点
- 根据模板，从答案节点开始反向推理，得到所有的 anchor 节点
- 由 anchor 节点再进行知识图推理，得到答案节点的集合
- 对答案节点之外的节点进行负采样，构建非答案节点的集合
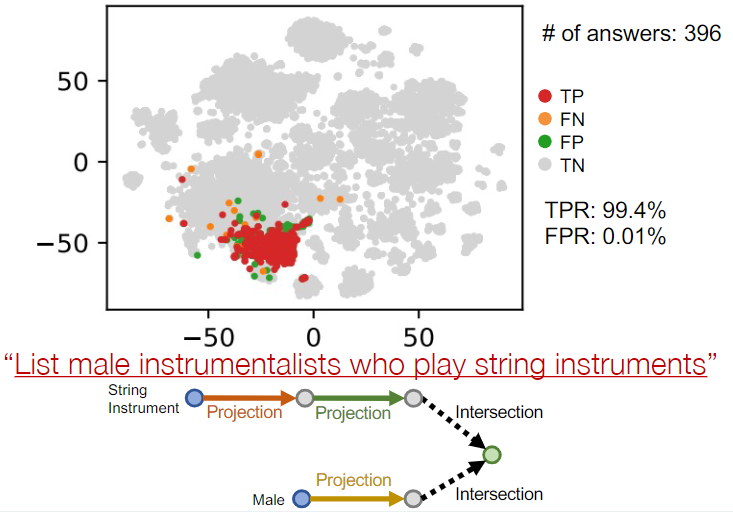
应用示例："列出所有使用弦乐器演奏的男性乐器演奏家"
