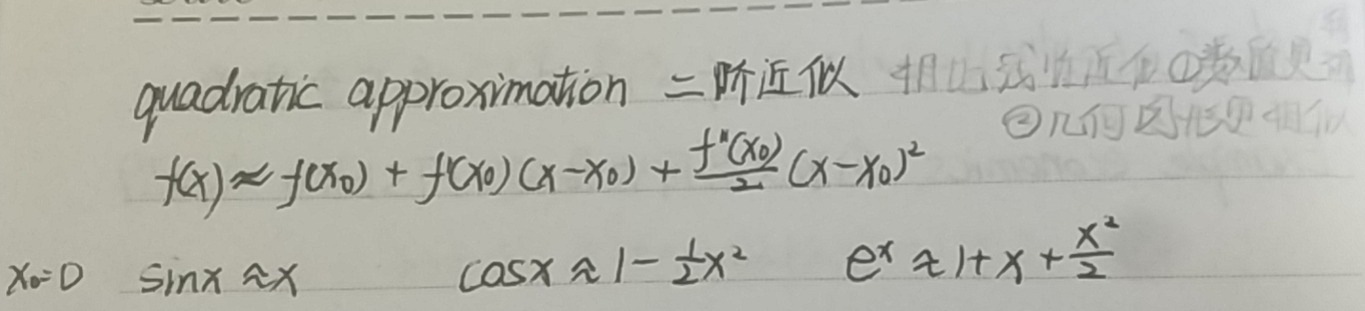1 线性近似 linear approximation
$$f(x) \approx f(x_0)+f'(x_0)(x-x_0)$$
- 其中$\approx$仅在$x$接近$x_0$时成立
以$x_0=0$且$x\approx 0$为前提,几种常见的函数线性近似:
- $sin(x) \approx x$
- $cos(x) \approx 1$
- $e^x \approx 1+x$
- $lm(1+x) \approx x$
- $(1+x)^r \approx 1+rx$
线性近似能起到简化函数的作用
2 线性近似举例
例题 $$\begin{align} e^{-3x}(1+x)^{\frac{-1}{2}} & \approx (1-3x)(1-\frac{1}{2}x) \ \\ & = 1-3x-\frac{1}{2}x+\frac{3}{2}x^2 \ \\
\text {忽略二次项可得}
\ \\ & \approx 1-\frac{7}{2}x \end{align}$$
应用-GPS信号偏移补偿
- 狭义相对论(special relativity)存在时间膨胀(time dilation)的概念
- 卫星距离地面过远,需要考虑修正时间膨胀导致的误差
- 修正方法为$T'=\frac{T}{\sqrt{1-\frac{v^2}{c^2}}}$,其中$c$表示光速
- 直接修正$T$计算量太大,可以考虑近似计算
- 令$u=\frac{v^2}{c^2}$,代入上式可得
$$T'=\frac{T}{\sqrt{1-u}}=T(1-u)^{\frac{-1}{2}} \approx T(1+\frac{1}{2}u)$$
- 设计GPS的工程师利用$T'=T(1+\frac{1}{2}\frac{v^2}{c^2})$
- 判断时间差和卫星发出电磁波的频率改变
- 然后进行信号偏移的补偿,使人们更好地接收信号
3 二阶线性 quadratic approximation
$$f(x) \approx f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2}(x-x_0)^2$$
- 相比于线性近似,二阶近似所得数值更精确
- 相比于线性近似,二阶近似所得几何图像与原图像更相似
- 相比于线性近似,二阶近似所需消耗的计算量更多
以$x_0=0$且$x\approx 0$为前提,几种常见的函数二阶近似:
- $sin(x) \approx x$
- $cos(x) \approx 1-\frac{1}{2}x^2$
- $e^x \approx 1+x+\frac{x^2}{2}$
- $lm(1+x) \approx x-\frac{1}{2}x^2$
- $(1+x)^r \approx 1+rx+\frac{r(r-1)}{2}x^2$
4 参考