1 数值积分
用于处理没有解析解的积分问题
常见的方法有三种
- Riemann Sums 黎曼和
- trapezoidal rule 梯形法
- Simpson‘s Rule 辛普森公式
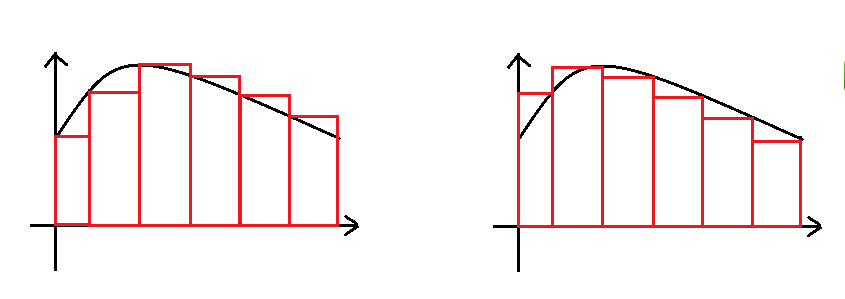
2 黎曼和
将区间等长分为n段,然后用矩形去逼近函数
$左和=(y_0+y_1+...+y_{n-1})\Delta x$
$右和=(y_1+y_2+...+y_{n})\Delta x$
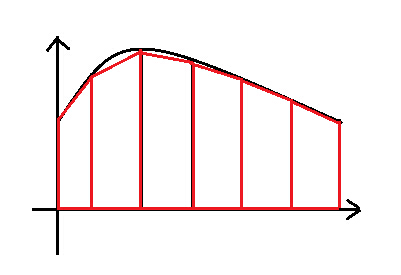
3 梯形法
用梯形去逼近函数,精度比黎曼和方法高
$$S=\Delta x(\frac{y_0+y_1}{2}+\frac{y_1+y_2}{2}+...+\frac{y_{n-1}+y_n}{2})=\Delta x(\frac{y_0}{2}+y_1+...+y_{n-1}+\frac{y_n}{2})$$
上式的结果其实为:黎曼左和与黎曼右和的平均值
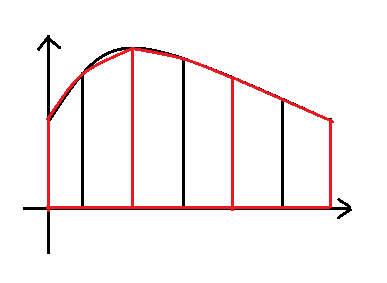
4 辛普森公式
用抛物线去逼近函数,精度比梯形法高
具体来说,首先 n 必须为偶数,将整个区间分为$\frac{n}{2}$段
每段的底为$2\Delta x$,高为$\frac{y_0+4y_1+y_2}{6}$(可理解为特殊的加权平均)
$$S=\frac{2\Delta x}{6}(y_0+4y_1+2y_2+4y_3+2y_4+...+2y_{n-2}+4y_{n-1}+y_n)$$
5 参考
