1 多层感知机
线性意味着单调假设: 任何特征的单向变化都会导致模型输出的单向变化
感知机(perceptron):最早的AI模型之一,不能解决诸如XOR(异或)的问题
感知机vs逻辑回归
- 损失函数两者不同:逻辑回归使用极大似然(对数损失函数),感知机使用的是最小化均方损失函数(即误分类点到超平面的距离总和)
- 激活函数不同:逻辑回归的sigmoid函数使得结果具有概率解释性,优于感知器的阶跃函数(分段函数)
多层感知机(multilayer perceptron):通过在网络中加入一个或多个隐藏层来克服线性模型的限制,可解决XOR问题,但模型的参数开销过高
线性激活函数的多层感知机等价于单层感知机(线性方程的叠加不变性)
常用激活函数:sigmoid、tanh、relu、softmax(处理多分类)
Relu函数:减轻神经网络的梯度消失问题;变体很多,计算成本很低,简单常用
多层感知机的非线性主要来自于隐藏层与激活函数
宽度神经网络vs深度神经网络
- 宽度神经网络实践中非常容易过拟合
- 深度神经网络的层次更符合从具体到抽象的认知过程
2 多层感知机实现(pytorch)
2.1 从零开始版本
import torch
from torch import nn
from d2l import torch as d2l
# 加载数据-迭代器
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
# 初始化模型参数
num_inputs, num_outputs, num_hiddens = 784, 10, 256
W1 = nn.Parameter(torch.randn(
num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(
num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
params = [W1, b1, W2, b2]
def relu(X):
"激活函数"
a = torch.zeros_like(X)
return torch.max(X, a)
def net(X):
"模型"
X = X.reshape((-1, num_inputs))
H = relu(X@W1 + b1) # 这里“@”代表矩阵乘法
return (H@W2 + b2)
loss = nn.CrossEntropyLoss() # 损失函数
# 训练
num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
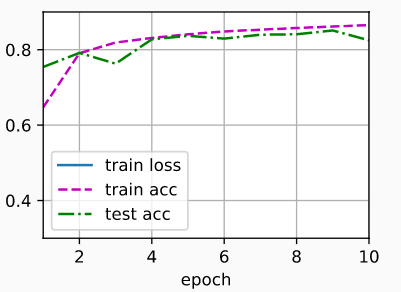
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)
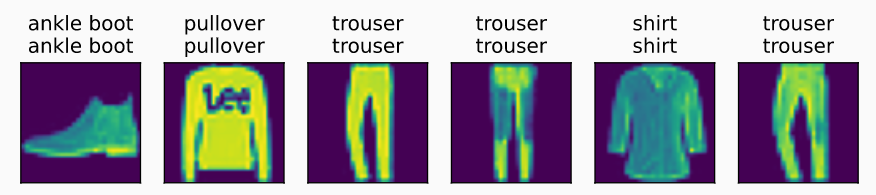
# 预测
d2l.predict_ch3(net, test_iter)
2.2 神经网络版本
import torch
from torch import nn
from d2l import torch as d2l
# 本小节和第三章5.2部分基本相同,只是微调了模型结构
net = nn.Sequential(nn.Flatten(),
nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights);
batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss()
trainer = torch.optim.SGD(net.parameters(), lr=lr)
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
3 多层感知机实现(tensorflow)
3.1 从零开始版本
import tensorflow as tf
from d2l import tensorflow as d2l
# 加载数据-迭代器
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
# 初始化模型参数
num_inputs, num_outputs, num_hiddens = 784, 10, 256
W1 = tf.Variable(tf.random.normal(
shape=(num_inputs, num_hiddens), mean=0, stddev=0.01))
b1 = tf.Variable(tf.zeros(num_hiddens))
W2 = tf.Variable(tf.random.normal(
shape=(num_hiddens, num_outputs), mean=0, stddev=0.01))
b2 = tf.Variable(tf.zeros(num_outputs))
params = [W1, b1, W2, b2]
def relu(X):
"激活函数"
return tf.math.maximum(X, 0)
def net(X):
"模型"
X = tf.reshape(X, (-1, num_inputs))
H = relu(tf.matmul(X, W1) + b1)
return tf.matmul(H, W2) + b2
def loss(y_hat, y):
"损失函数"
return tf.losses.sparse_categorical_crossentropy(
y, y_hat, from_logits=True)
# 训练
num_epochs, lr = 10, 0.1
updater = d2l.Updater([W1, W2, b1, b2], lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)
# 预测
d2l.predict_ch3(net, test_iter)
3.2 神经网络版本
import tensorflow as tf
from d2l import tensorflow as d2l
# 本小节和第三章6.2部分基本相同,只是微调了模型结构
net = tf.keras.models.Sequential([
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(256, activation='relu'),
tf.keras.layers.Dense(10)])
batch_size, lr, num_epochs = 256, 0.1, 10
loss = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
trainer = tf.keras.optimizers.SGD(learning_rate=lr)
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
4 欠拟合和过拟合
正则化(regularization):对抗过拟合(overfitting)的技术
训练误差(training error):模型在训练数据集上计算得到的误差
泛化误差(generalization error): 模型应用在测试集上的误差的期望值,测试集和训练集需要保持数据分布的一致性,即独立同分布假设(i.i.d. assumption)
影响模型泛化能力的几种因素:
- 可调参数的数量过多
- 权重的取值范围过大
- 训练样本的数量过少
K 折交叉验证:原始数据被分成 K 个不重叠的子集。 然后执行 K 次训练和验证,每次在 K−1 个子集上进行训练, 并在剩余的一个子集上进行验证。 最后,取 K 次实验的结果平均来估计训练和验证误差。
K 折交叉验证不适合数据量太大的情况
欠拟合vs过拟合
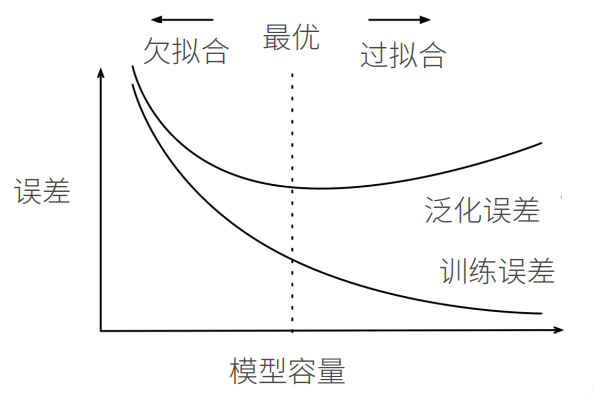
实践技巧:先确保充分的模型容量,再考虑简化与调优
决定模型容量的两个关键因素
- 参数个数
- 参数值的可选范围
- 参数个数及其可选范围越宽广,最终的模型才能保证足够的多样性,而这种多样性即是模型的复杂度,也是模型的拟合能力(容量)
统计学习的核心理论-VC维
- 对于一个分类模型,VC等于一个最大的数据集的大小,对于数据的任意标注方式,都存在一个模型能将其完美分类(吐槽一句:现实中这种情况一般都是严重过拟合;而且真实数据集一般都是接近无限的~)
- VC维提供了一个模型为什么好的理论依据,但是在深度学习中不太常用,因为只是理论依据,而且深度学习模型计算VC维的成本较高
- 比如支持N维输入的感知机的VC维是N+1,所以2维输入的感知机的VC维是3,所以对于大小为4的数据集,存在无法完美拟合的情况(比如XOR问题)
- 不过一般多层感知机的VC维是$O(Nlog_2N)$
5 权重衰减
权重衰减(weight decay),也被称为$L_2$正则化
将范数作为惩罚项加到最小化损失的问题中,以此来限制权重向量的复杂度
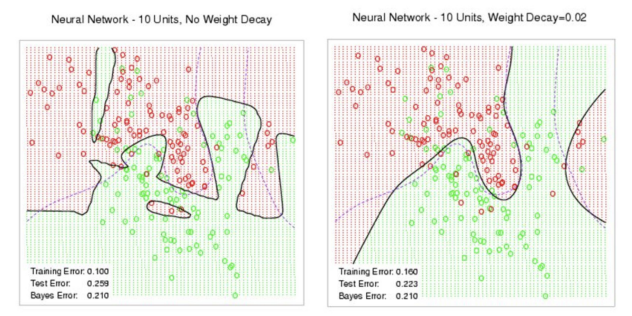
加入正则化后的梯度更新:

代码实践,只需要在损失函数中加入正则项即可。具体代码略,详见原书。
6 Dropout
Dropout也被称为暂退法、丢弃法。通过在网络层之间加入噪音增强模型的鲁棒性。
Dropout所起到的作用和正则化方法是类似的,比如Tikhonov正则就等价于使用带噪音的数据。
Dropout常作用于隐藏全连接层,会对每一个激活函数的输出值进行随机丢弃,方式如下:
$$\begin{equation} x_i' = \left\{ \begin{array}{rl} 0 & with \ \ probablity \ \ p \\ \\ \frac{x_i}{1-p} & otherise \end{array} \right. \end{equation}$$ 这种将输出项随机置0的方式能显著控制模型的复杂度,常用值为0.1、0.5、0.9
Pytorch 版本自定义Dropout层
import torch
from torch import nn
from d2l import torch as d2l
def dropout_layer(X, dropout):
assert 0 <= dropout <= 1
# 在本情况中,所有元素都被丢弃
if dropout == 1:
return torch.zeros_like(X)
# 在本情况中,所有元素都被保留
if dropout == 0:
return X
mask = (torch.rand(X.shape) > dropout).float()
return mask * X / (1.0 - dropout)
X= torch.arange(16, dtype = torch.float32).reshape((2, 8))
print(X)
print(dropout_layer(X, 0.5))
# nn.Dropout(0.5) 相应的API函数
Tensorflow 版本自定义Dropout层
import tensorflow as tf
from d2l import tensorflow as d2l
def dropout_layer(X, dropout):
assert 0 <= dropout <= 1
# 在本情况中,所有元素都被丢弃
if dropout == 1:
return tf.zeros_like(X)
# 在本情况中,所有元素都被保留
if dropout == 0:
return X
mask = tf.random.uniform(
shape=tf.shape(X), minval=0, maxval=1) < 1 - dropout
return tf.cast(mask, dtype=tf.float32) * X / (1.0 - dropout)
X = tf.reshape(tf.range(16, dtype=tf.float32), (2, 8))
print(X)
print(dropout_layer(X, 0.5))
# tf.keras.layers.Dropout(0.5) 相应的API函数
7 模型训练与计算图
神经网络模型的训练主要依靠前向传播(forward propagation)算法和反向传播(backward propagation)算法,并且其中存在着大量梯度的自动计算(自动微分)。
以一个简单的双层神经网络为例,其对应的前向传播计算图如下:
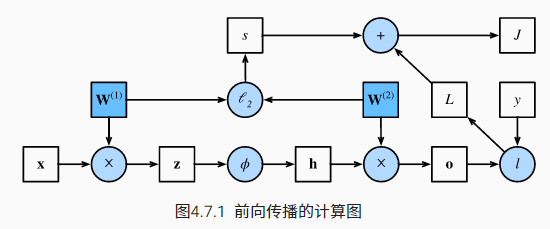
其中$x$表示输入,$W^{(1)}$表示输入层权重,$z=W^{(1)}x$,其经过激活函数映射后转化为隐藏层输出$h$, $W^{(2)}$表示输出层权重,$o=W^{(2)}h$表示输出,$l$表示损失函数,损失项$L=l(o,y)$
$\lambda$表示正则化超参,$s=\frac{\lambda}{2}(||W^{(1)}||_F^2+||W^{(2)}||_F^2)$表示正则项,目标函数$J=L+s$
反向传播算法的目的是计算梯度$\frac{\partial{J}}{\partial{W^{(1)}}}$和$\frac{\partial{J}}{\partial{W^{(2)}}}$,然后进行权重值的更新。反向传播时的计算顺序与前向传播相反,具体的计算主要借助链式法则来实现,反向传播能重复利用前向传播中存储的中间值,避免重复计算,但也会消耗更多的内存(考虑到计算速度的大幅提升,这种额外的内存消耗是非常划算的)~
8 模型稳定性
8.1 梯度消失与爆炸
假设神经网络的层数为$d$,其中第$t$层的正向传播过程为 $$h^t=f_t(h^{t-1})=\sigma(W^th^{t-1})$$ 而第$t$层的反向传播过程(求导)为 $$\frac{\partial{h^t}}{\partial{h^{t-1}}}=diag(\sigma'(W^th^{t-1}))(W^t)^T$$ 则从第$d$层到第$t$层的反向传播过程为 $$\prod_{i=t-1}^{d}\frac{\partial{h^i}}{\partial{h^{i-1}}}=\prod_{i=t-1}^{d}diag(\sigma'(W^ih^{i-1}))(W^i)^T$$ 此时可以发现,当神经网络层数足够多时,反向传播过程中会存在大量矩阵连乘的情况,这时传播中的梯度值就非常容易出现不稳定的情况,即梯度消失(gradient exploding)与梯度爆炸(gradient vanishing)
梯度消失:参数更新过小,在每次更新时几乎不会移动,导致模型无法学习
主要问题:梯度值变为0(尤其是16位浮点);无法有效训练;随着层数的加深,梯度消失问题会越来越严重
对于sigmoid函数来说,输入值过大或过小都容易导致梯度消失:
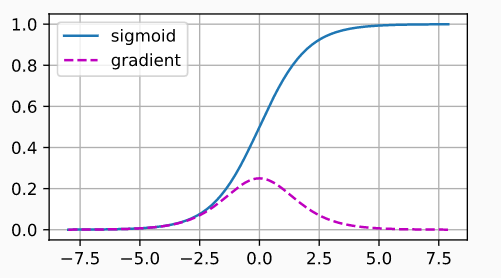
Relu函数能缓解梯度消失问题,并且加速收敛
梯度爆炸:参数更新过大,破坏了模型的稳定收敛
主要问题:容易超出值域(尤其是16位浮点数);对学习率敏感
8.2 提高模型稳定性
应对梯度消失或爆炸的问题,一个合理的方案是控制每一层的正向传播与反向传播过程中的传递向量,让均值为0,方差固定为常数:
$E[h_i^t]=0,E[\frac{\partial{l}}{\partial{h^t_i}}]=0,Var[h_i^t]=constant,Var[\frac{\partial{l}}{\partial{h^t_i}}]=constant$
这个方案可以通过合理的参数初始化和激活函数来实现
合理的参数初始化可以提高模型的稳定性,加快模型收敛;不合理参数初始化(全部初始化为0或同一个常数)可能导致模型无法有效训练。
假设: $w_{i,j}^t$之间是独立同分布(i.i.d)的,且$E[w_{i,j}^t]=0,Var[w_{i,j}^t]=\gamma_t$ $h_i^{t-1}$独立于$w_{i,j}^t$,先排除激活函数:$h^t=W^th^{t-1}$
对于正向传播过程,均值为0是可证的:
$$E[h_i^t]=E[\Sigma_jw_{i,j}^th_j^{t-1}]=\Sigma_jE[w_{i,j}^t]E[h_j^{t-1}]0$$
对于正向传播过程,要保证方差为常数,需要满足$n_{t-1}\gamma_t=1$,证明如下:
$$\begin{align}
Var[h_i^t]=E[(h_i^t)^2]-E[h_i^t]^2 & = E[(\Sigma_jw_{i,j}^th_j^{t-1})^2]-0
\ \\
& = \Sigma_jE[(w_{i,j}^t)^2]E[(h_j^{t-1})^2]
\ \\
& = \Sigma_jVar[w_{i,j}^t]Var[h_j^{t-1}]=n_{t-1}\gamma_tVar[h_j^{t-1}]
\end{align}$$
对于反向传播过程同理可知(证明略,同正向传播过程的证明类似),要保证均值为0且方差为常数,需要满足$n_t\gamma_t=1$
注意到,只有输入维度与输出维度一直相同时,以上两个条件才会都满足,而这一点在实际中是很难保证的,一个折中的方法是满足$\gamma_t(n_{t-1}+n_t)/2=1$,这就是实用的Xavier初始化方法的基本原理。
- Xavier+正态分布:$N(0,\sqrt{2/(n_{t-1},n_t)})$
- Xavier+均匀分布:$U(-\sqrt{6/(n_{t-1},n_t)},\sqrt{6/(n_{t-1},n_t)})$
刚刚的结论为不考虑激活函数的情况,若假设存在激活函数$\sigma(x)=\alpha x+\beta$ 此时$h^t=\sigma(h')=\sigma(W^th^{t-1})$,均值变为$E[h_i^t]=E[\alpha h_t'+\beta]$,方差变为: $$Var[h_i^t]=E[(h_i^t)^2]-E[h_i^t]^2=E[(\alpha h_i'+\beta)^2]-\beta^2=\alpha^2Var[h_i']$$ 所以若想继续保证均值为0,方差为常数,需要满足$\alpha=1,\beta=0$
即激活函数应该尽量贴近无偏移项的线性函数,根据此结论可以对激活函数进行修正。以$sigmoid$函数为例,其泰勒展开为$sigmoid(x)=\frac{1}{2}+\frac{x}{4}-\frac{x^3}{48}+O(x^5)$,为了尽可能贴近条件$\alpha=1,\beta=0$,可考虑对$sigmoid$函数进行修正: $$4\times sigmoid(x)-2$$ 其他常用的激活函数展开: $$tanh(x)=0+x-\frac{x^3}{3}+O(x^5)$$ $$relu(x)=0+x\ \ for\ x\geq0$$ 侧面验证了这两个激活函数相比于$sigmoid$函数的优越性
9 环境和分布偏移
环境和分布偏移是导致模型部署失效的重要原因
9.1 偏移的类型
偏移主要分三种:协变量(特征)偏移、标签偏移和概念偏移
场景1:在大学征集抽血用于疾病检测,这存在年龄导致的特征偏差
场景2:拿赛车游戏训练的模型用于自动驾驶,存在标签偏差
场景3:垃圾邮件过滤器随着时间的推移逐渐失效,存在时间导致的概念偏移
9.2 偏移的修正
特征偏差的修正(区分与加权):
- 假设训练集存在分布偏差,测试集接近真实分布
- 训练一个二分类模型$h$,用于区分训练集与测试集
- 根据二分类所得概率给训练集样本加权重$\beta_i=exp(h(x_i))$
- 接近测试集的样本权重高,背离测试集的样本权重低
- 最后进行带权重的模型训练,实现特征偏差的修正
标签偏差的修正(分布估计与加权):
- 假设训练数据存在有偏的标签分布$q$,测试数据存在标签真实分布$p$
- 先在源数据划分训练集和验证集,建立最优模型并计算混淆矩阵$C$
- 借助模型预测值的均值$\mu(\hat{y})$和逆矩阵$C^{-1}$估计分布$p(y)=C^{-1}\mu(\hat{y})$
- 对标签为$y_i$的训练数据添加权重$p(y_i)/q(y_i)$并进行训练,实现标签偏差的修正
概念偏差的修正:定时更新、在线学习、多模型选择、特征丰富等等