中文标题:Treeformer:用于高效注意力计算的密集梯度树
英文标题:Treeformer: Dense Gradient Trees for Efficient Attention Computation
发布平台:ICLR
International Conference on Learning Representations
发布日期:2023-03-17
引用量(非实时):3
DOI:10.48550/arXiv.2208.09015
作者:Lovish Madaan, Srinadh Bhojanapalli, Himanshu Jain, Prateek Jain
关键字: #Treeformer #高效计算
文章类型:preprint
品读时间:2023-09-04 15:35
1 文章萃取
1.1 核心观点
- 本文将注意力计算转化为基于决策树的最近邻检索问题,并提出了一种全新的注意力架构 TreeFormer——给定查询后使用密集梯度树来检索需要关注的TopK键
之后,本文使用决策树开发了两种新颖的注意机制:对于给定的查询,TF-ATTENTION 仅关注与查询匹配到同一叶节点中的键;TC-ATTENTION 则关注曾经过查询路径的所有键。此外,本文还开发了一种bootstrapping+自监督学习方法来逐步训练TreeFormer模型的稀疏注意力层,从而表明可以使用反向传播将决策树训练为神经网络的一部分。
最后,本文通过实验证明了 TreeFormer 架构的有效性,TF-ATTENTION 和 TC-ATTENTION 都实现了与基线 Transformer 架构相匹配的精度;并且相比于标准 Transformer,TreeFormer 的注意力层计算成本( FLOPs)降低了 30 多倍,与 SOTA BigBird 相比,成本降低了 9 倍
1.2 综合评价
- 利用决策树的天然检索能力替代或简化注意力机制的权重计算
- 将决策树的参数学习融合到了神经网络的训练过程
- 部分公式或符号定义不够完善,训练部分的描述略显模糊
- 实验分析较为全面,但缺少训练时间上的对比(重要)
- 存在较多的探索和改善的空间,可考虑进一步与图结构融合
1.3 主观评分:⭐⭐⭐⭐
2 精读笔记
2.1 背景知识
标准注意力定义:
- $Q\in R^{n \times d}$是输入查询(query)矩阵、$K\in R^{n \times d}$是输入键(key)矩阵、$V\in R^{n \times d}$是输入值(value)矩阵;其中$n$表示序列长度,$d$表示嵌入维度
- $W^Q,W^K,W^V \in R^{d \times d}$分别是$Q,K,V$的投影矩阵(系数矩阵)
- 每个 Transformer 层中的标准注意力可以定义为
$$Attention(Q,K,V)=softmax[\frac{QW^Q(KW^K)^T}{\sqrt{d}}]\cdot VW^V=A\cdot VW^V$$
上式的计算复杂度为$O(n^2d+d^2n)$;当序列长度$n$较大时,该计算方式可能会成为算力的主要瓶颈;过往的方式一般都是利用不同稀疏模式的注意力机制降低计算成本,或者使用低秩近似等近似计算方法降低计算成本。 本文则提出了一种基于决策树的注意力机制,将计算复杂度加速到$O(nh)$,其中 h 是决策树的高度
不同模型的注意力计算成本对比:

- Linformer:通过增加额外线性投影的方式对原始注意力进行低秩因数分解($k$表示投影维度),使得注意力机制的空间和时间复杂度降低为一个$O(n)$操作
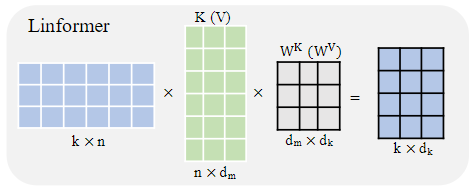
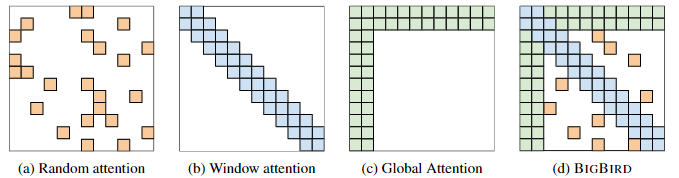
- BigBird:该模型的稀疏注意力仅考虑部分全局注意力+滑动窗口(局部)注意力+随机注意力,将算法复杂度降低线性,同时模型可处理的序列长度提升了8倍
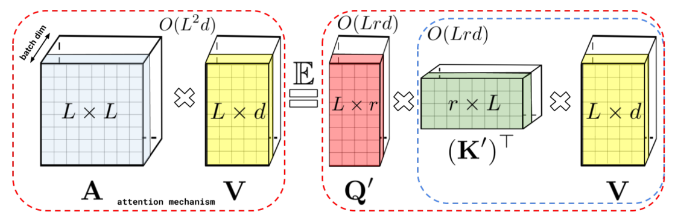
- Performer:使用一种新的快速注意方法(FAVOR+),将注意力矩阵A低秩分解得到解耦矩阵Q′和K′,并按顺序进行矩阵乘法,以线性复杂度实现注意力矩阵A的近似
决策树算法基础拓展:决策树基础
本文决策树的符号定义:
- $\mathcal{T}(\theta)$表示一个高为$h$,节点数为$2^h$的二叉树
- $\theta_{l,j}$表示二叉树第$l\in {0,1,...,h}$行的第$j \in {0,1,...,2^l-1}$个节点的参数
- 每个树的节点内部都有一个分类器$f_{l,j}(q)=f(\theta_{l,j};q)=<w_{l,j},q>+b_{l,j}$,用于确定将输入查询$q$发送到哪个子节点(左子节点 or 右子节点)
- $P_{\mathcal{T}}(l,q)$表示当输入查询为$q$时在第$l$层遍历节点后所得到的节点索引;令$l$从$0$逐渐增加到$h$,对应的$P_{\mathcal{T}}(l,q)$描述了输入查询$q$在决策树中自上而下的游走路径
- $S_{{l,j}}(K)$表示当经过节点${l,j}$时,对应键(key)矩阵$K$的向量索引集合;矩阵$K$中每一个键向量也都会有一条在决策树中自上而下的游走路径;$S_{{l,j}}(K)$返回了所有会经过节点${l,j}$的键向量的索引集合
$i \in S_{{l,j}}(K)$当且仅当$j=P_{\mathcal{T}}(l,k_i)$
2.2 TreeFormer 变体
传统的注意力计算公式: $$Attention(q_i,K,V)=softmax[\frac{q_i^T W^Q (KW^K)^T}{\sqrt{d}}]\cdot VW^V$$
传统的注意力计算会关注所有的键值(线性扫描),并根据每个输入$q_i$计算与不同键$k$的相似度,以此作为权重对值$v$进行加权平均。而最近的工作表明:
- 不需要关注给定输入序列中的所有标记(Shi et al., 2021)
- top-k 注意力是标准注意力的良好近似(Gupta et al., 2021)
因此,本文提出了两种基于决策树的分层导航方法来取代线性扫描,每次检索最相似的TopK个键;同时也对决策树的参数进行优化,以更好地优化损失函数
2.2.1 TF-ATTENTION (Tree Fine-grained Attention)
变种1:仅考虑与查询$q$属于同一叶子节点的键,这些键集合构成了Topk相似键
$$TF_-Attention(q_i,K,V;\mathcal{T})=softmax[\frac{q_i^T W^Q (K_{\overline{S}}W^K)^T}{\sqrt{d}}]\cdot V_{\overline{S}}W^V$$
- 其中$\overline{S}=S_{h,P_{\mathcal{T}}(h,(W^Q)^Tq_i)}(KW^K)$,表示与查询$q_i$映射到同一叶节点的键集合
- 该变种是稀疏注意力的一种,对于和查询$q$不属于同一叶节点的键,其注意力得分默认为0
- 树结构负责找出给定查询$q$后最重要(属于同一叶节点)的TopK键集合
- TopK键集合的元素数量是不确定的,由决策树自动给出
算法复杂度分析:
- 假设叶子节点是均匀分布的,则计算成本为$O(n^2d/2^h)+2cd^2n=O(nkd)+2cd^2n$
- 其中$k$是小常数,间接描述了决策树高度$O(log(n/k))$;$c$描述了两矩阵乘法计算的成本
- 假设叶子节点是极度不均衡的(查询和键集合都集中在一个叶子节点)
- 此时 TF-ATTENTION 退化为普通注意力计算,对应的计算成本为$O(n^2d+d^2n)$
算法的改进:k-ary TF-ATTENTION
- 扩展二叉树结构,每个节点可拓展的子节点改为$b_l$
- 该拓展可以在高度$h$较小的情况下,缩放叶子节点的数量
算法的缺点:
- 查询和键向量的分布可能是非均匀的,导致计算成本逼近传统注意力机制;此时可考虑增加显式的损失项,约束决策树结构,鼓励不同叶子节点之间进行更合理的表示/区分度
- 给定查询的关键信息可以存在不同的叶子节点中;但由于算法的稀疏性,查询和不同叶子节点之间的注意力分数会强制为0;此时考虑多个决策树(森林结构)可能有助于缓解这种情况
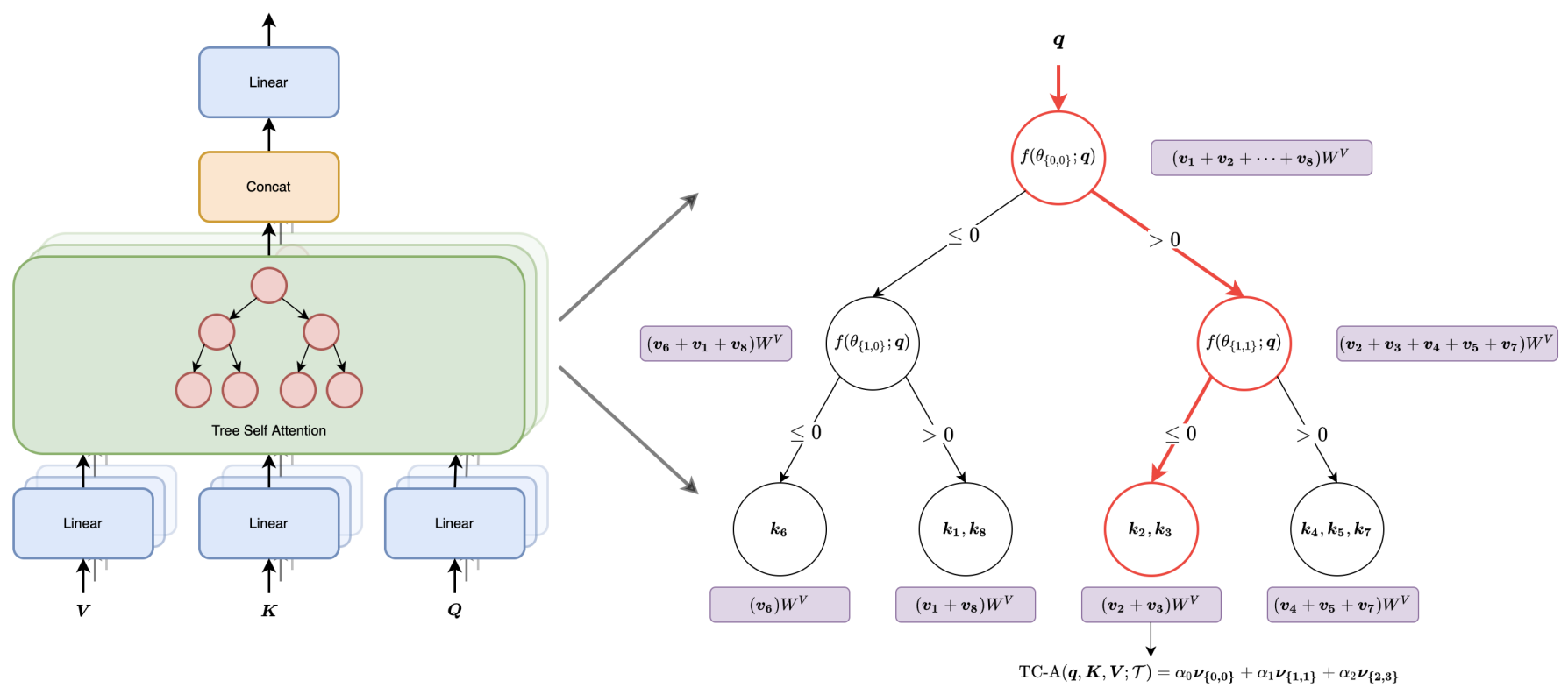
2.2.2 TC-ATTENTION (Tree Coarse Attention)
变体2:不再计算注意力权重,查询仅用于导航到叶子节点,注意力得分是对应叶子节点的值向量均值(固定值,所以注意力分数的计算不再直接依赖查询$q$);
TF-ATTENTION更倾向于将所有键映射到一个叶子节点,而TC-ATTENTION的激励则完全相反;TC-ATTENTION追求通过树结构来容纳注意力权重信息,因此更愿意在叶子节点中尽可能分散键
$$\begin{align} TC_-Attention(q_i,K,V;\mathcal{T}) & = \Sigma_{l=0}^h \alpha_l \cdot v_{{l,P_{\mathcal{T}}(l,(W^Q)^Tq)}} \ \\ v_{l,j} & = \frac{1}{|S_{l,j}(KW^k)|}\Sigma_{i\in S_{l,j}(KW^k)}V_iW^V \ \\ \end{align}$$
- 其中$v_{l,j}$是所有经过节点${l,j}$的值向量的均值
- $\alpha_l$是决策树内部每一层对应的可学习参数,用来表示不同层的注意力权重
算法复杂度分析:
- 第一部分是查询、键、值的投影变换(参数矩阵),由于查询矩阵和键矩阵共用一套投影参数,因此对应计算成本为$O(cd^2n/2)$,只有传统注意力的一半
- 第二部分是计算存储值向量的投影变换,对应计算成本为$O((2^{h+1}-1)d)$
- 第三部分是计算所有查询$Q$的路径及其注意力转换,对应计算成本为$O(ndh)$
- 最终 TC-ATTENTION 的计算复杂度为$O(ndh+(2^{h+1}-1)d+d^2n)$
在后续的实验过程中,树的深度$h$通常小于10
2.2.3 Treeformer模型的训练
使用增量 bootstrapping 方法来训练 Treeformer,伪代码如下:

- 首先使用预训练的现有模型(比如Transformer或者BigBird),之后在最后几层(第j到L层)引入基于树的注意力机制(TF-ATTENTION 或 TC-ATTENTION)
- $M_{{j,...,L}}$表示需要训练的新架构,新架构使用标准自监督学习的方式进行固定次数的训练
- 之后使用$M_{{j,...,L}}$的参数初始化$M_{{i,...,j,...,L}}$,其中第${i,...,j-1}$层的参数初始值是由下一层的参数值随机分配而得(此处也可以尝试其他 bootstrapping 方法,但本文未探索)
- 之后再训练$M_{{i,...,j,...,L}}$,然后继续往上扩展,以此类推直到完成$M_{{1,...,L}}$的完整训练
在面向下游任务进行微调(fine-tuning)时,不再进行 bootstrapping;因为根据实验分析,这时进行 bootstrapping式微调和普通微调方法没有显著差异
2.3 实验分析
不同架构模型在各项任务中的性能表现:
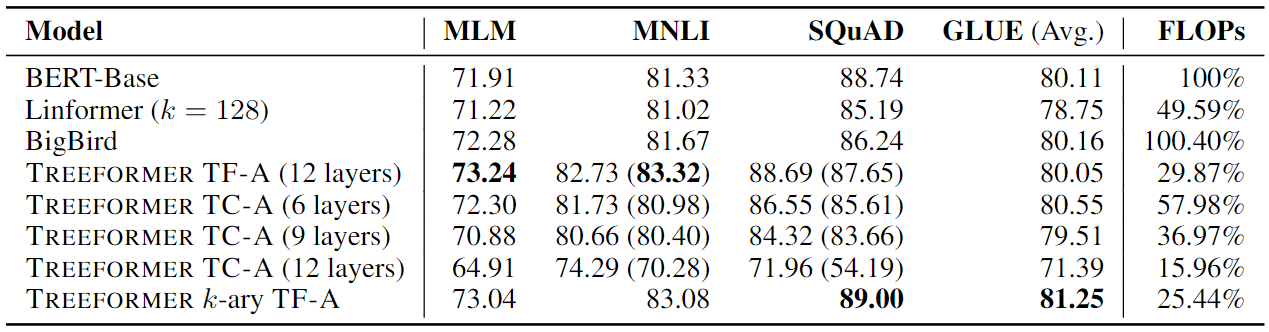
- MLM 表示随机遮盖预测任务;MNLI 表示文本推理任务
- SQuAD 表示文本问答任务;GLUE 是一项综合的基准测试
- TreeFormer 模型使用较少的 FLOPs(总浮点运算数)击败了其他模型
- 随着 TC-ATTENTION 层数量的增加,TreeFormer模型的准确性显着下降
TreeFormer 模型的训练过程:
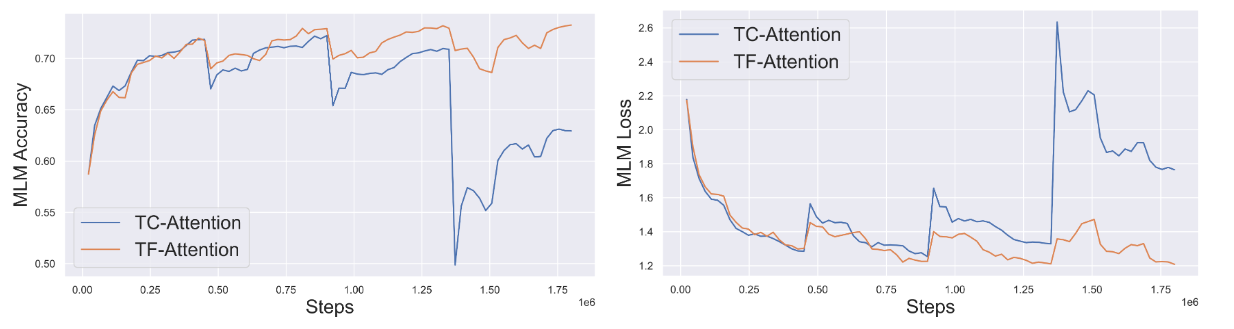
- MLM 准确性(损失)的突然下降(增加)发生在 bootstrapping 阶段,即用决策树层数较少的模型初始化决策树层数较多的模型时;但最终会导致 TF-A 的最终精度更高
- TC-A引导最多 6 个决策树层(直到 ≈ 1e6 步)有所改进,但继续增加决策树层受益会逐渐消失直至恶化,当决策树层数达到 12 时会存在训练不稳定的问题
不同深度的 TreeFormer 模型的训练过程对比:
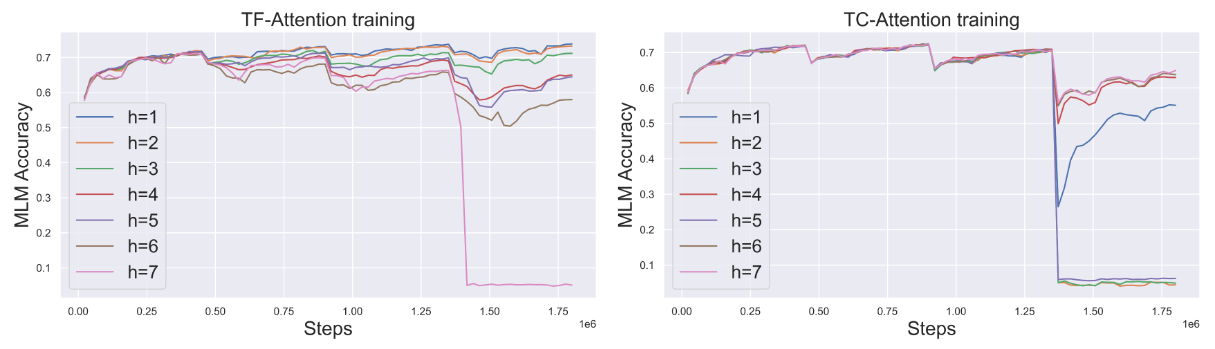
- 当树高度较小时,TF-A 在bootstrapping 时表现更好,但当树高度达到 7 时,效果会受到影响
- 对于较大的高度(超过 6 层,共 12 层),由于梯度消失,并且 MLM 准确度在bootstrapping 过程的最后阶段接近 0,因此TC的训练会很困难
TreeFormer模型不同层的叶子节点中关键向量的分布:
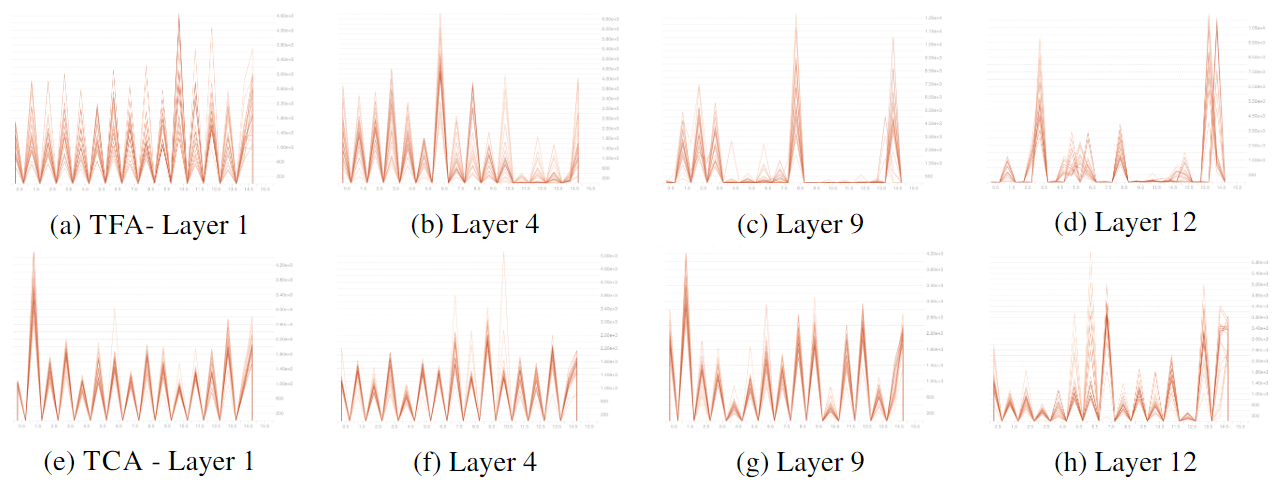
- 较浅的线代表预训练过程的初始阶段,较暗的线代表预训练后期的分布
- 与模型浅层(Layer 1)中的节点分布相比,深层(Layer 12)的关键向量分布更偏斜
- 与 TC-A 相比,TF-A 变体的分布更加偏斜(稀疏注意力,更关注与查询相关的键)
不同架构在LRA基准测试中的对比:
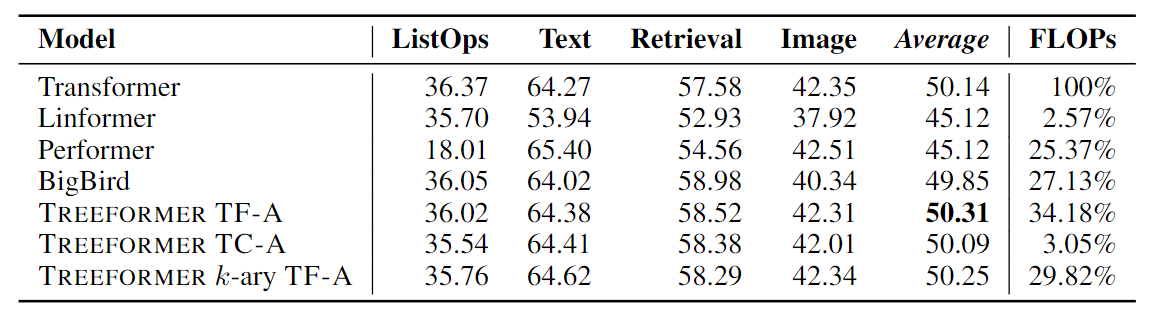
- LRA 是一个针对高效 Transformer 基准测试,关注长语境场景下的模型质量评估
- LRA 包含六项基准测试(3项文本类,3项图像类),本次实验删除了其中的 Pathfinder 任务(准确率差异大)和 Path-X(序列过长,所有模型都无法执行)
- 剩余的任务中,TreeFormer 实现了和其他任务相似的准确率,但 FLOPs 低很多
不同序列长度的模型对比:

- 序列越长,TreeFormer 的优势越明显;相比普通 Transformer,提速在1.8x~6.7x