循环神经网络(RNNs):具有隐状态、不同层参数共享的神经网络
常见的三种基础 RNNs :RNN、GRU、LSTM
RNN
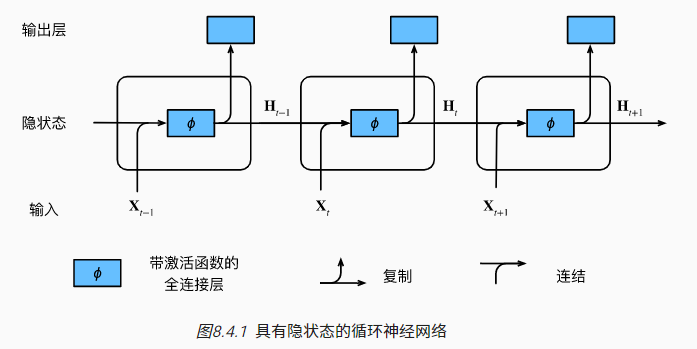
隐变量模型:使用隐状态 $h_{t-1}$ 存储前 $t-1$ 步的序列信息 $$P(x_t|x_{t-1},...,x_1)\approx P(x_t|h_{t-1})$$ $$h_t=f(x_t,h_{t-1})$$ 循环神经网络(recurrent neural networks,RNNs) 是具有隐状态的神经网络
假设时刻 $t$ 的输入为 $X_t \in \mathbb{R}^{n\times d}$,对应的权重参数为 $W_{xh}$,前 $t-1$ 时刻积累的隐状态为 $H_{t-1}\in \mathbb{R}^{n\times h}$,对应的权重参数为 $W_{hh}$,偏置为 $b$。则此 RNN 隐藏层计算可表示如下: $$H_t=\phi(X_tW_{xh}+H_{t-1}W_{hh}+b_h)$$ 输出层计算可表示如下: $$O_t=H_tW_{hq}+b_q$$ 其中 $\phi$ 表示激活函数,模型的可训练参数包括 $W$ 和 $b$,参数下标表示参数对应的维度
GRU
GRU 在 RNN 的基础上增加了针对隐状态的门控:
- 更新门(update gate)用于确定隐状态是否需要更新,有助于捕捉序列中的长期依赖
- 重置门(reset gate)用于确定隐状态是否需要重置,有助于捕捉序列中的短期依赖
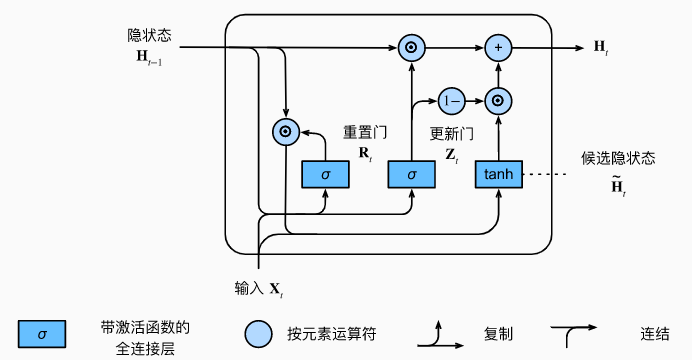
假设时刻 $t$ 时的批次输入为 $X_t\in \mathbb{R}^{n\times d}$,上一时刻的最终隐状态为 $H_{t-1}\in \mathbb{R}^{n\times h}$。则重置门 $R_t\in \mathbb{R}^{n\times d}$ 和更新门 $Z_t\in \mathbb{R}^{n\times d}$ 的计算方式如下: $$\begin{equation} \left\{ \begin{gathered} R_t=\sigma(X_tW_{xr}+H_{t-1}W_{hr}+b_r) \ \\ Z_t=\sigma(X_tW_{xz}+H_{t-1}W_{hz}+b_z) \end{gathered} \right. \end{equation}$$ 其中 $W_{xr},W_{xz}\in \mathbb{R}^{d×h}$ 和 $W_{hr},W_{hz}\in \mathbb{R}^{h×h}$ 是权重参数,$b_r,b_z\in \mathbb{R}^{1\times h}$ 是偏置项
时刻 $t$ 时的候选隐状态(candidate hidden state) $\widetilde{H}t\in \mathbb{R}^{n\times h}$ 计算如下: $$\widetilde{H}_t=tanh(X_tW\{xh}+(R_t\odot H_{t-1})W_{hh}+b_h)$$ 其中 $W_{xh}\in \mathbb{R}^{d×h}$ 和 $W_{hh}\in \mathbb{R}^{h×h}$ 是权重参数,$b_h\in \mathbb{R}^{1\times h}$ 是偏置项,$\odot$ 是哈达玛积 (Hadamard product,即同阶矩阵间对应元素相乘)
时刻 $t$ 时的最终隐状态 $H_t\in \mathbb{R}^{n\times h}$ 计算如下: $$H_t=Z_t\odot H_{t-1}+(1-Z_t)\odot \widetilde{H}_t$$
当 $Z_t$ 接近 1 时,模型倾向于保留旧状态;当 $Z_t$ 接近 0 时,模型倾向于保留当前状态
LSTM
长短期记忆网络引入了记忆元(memory cell,其实可以看作为隐状态的一种特殊类型),简称单元(cell),通过三种门控制记忆元的输入、输出和遗忘:
- 输出门(output gate):控制记忆元存储数据的输出
- 输入门(input gate):决定何时将数据存入记忆元
- 遗忘门(forget gate):管理记忆元存储内容的重置
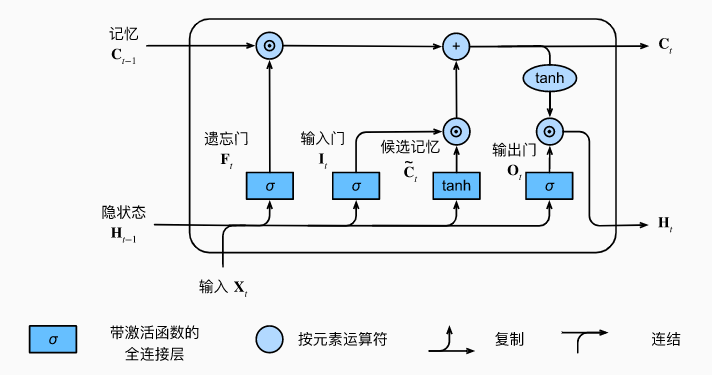
具体计算过程和 GRU 非常相似,只不过细节上略有调整,比如 $\widetilde{H}_t,H_t$ 转为 $\widetilde{C}_t,C_t$
因此,就暂时略过了(敲公式快敲麻了)