中文标题:统计建模的两种文化
英文标题:Statistical Modeling: The Two Cultures
发布平台:Statist. Sci.
发布日期:2001-08-01
引用量(非实时):4927
DOI:10.1214/ss/1009213726
作者:Leo Breiman
关键字: #Statistical #数据模型 #算法模型 #LeoBreiman
文章类型:journalArticle
品读时间:2021-09-01 14:44
1 文章萃取
1.1 核心观点
目前在统计建模领域有两种文化。一种是假设数据的生成过程是一个随机的数据模型,而另一种则认为数据的内部机制是未知,需要通过算法建模。
统计学家一直致力于尽量使用数据模型,而催生了很多不相关的理论和可疑的结论,也导致了面对很多有趣问题面前的局限性。相反的,算法建模理论和实践在统计以外的领域发展迅速。因为它既可以应对大型而复杂的数据集,相比于数据建模,也可以在较小数据集上实现更精确和信息更丰富的替代。
如果我们的目标是使用数据来解决问题,那么我们就需要摆脱对数据模型的独占依赖,不拘一格,选择更多样化的理论方法和工具。
1.2 综合评价
- 非常精彩 言简意赅 例子详实
- 很有预见性的看到了机器学习的趋势
- 一针见血地强烈抨击了统计界的固执己见
1.3 评分:⭐⭐⭐⭐⭐
2 精读笔记
2.1 data model vs algorithm model
统计学研究变量之间的关系,比如x和y之间的关系。

统计学在分析数据时有两个目标:
- Prediction,即给一个x,对应的y是什么(产生式?)
- Information,或者说就是x和y之间的关系,x生成到y的过程(生成式?)
那想要达到这两个目标有两种方式:
- data model,98%的统计学家使用这种方式

- algorithm model,2%的统计学家使用这种方式
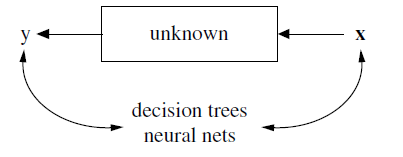
data model 会假定x到y的关系:
- 比如在linear regression中假设是线性关系,误差符合高斯分布
data model的过往成功导致了统计学过度focus在传统方式,导致了一系列问题:
- 对于有些问题,当前的模型并不适用,并会得出不靠谱的结论
- 可能导致统计学家固步自封,不研究更适合于复杂问题的model
2.2 我是如何走上现代统计模型这条路的?
我先在学术圈呆了7年,然后去商业圈做了13年的咨询,然后回归学术圈。
就是在商业圈这13年,奠定了我走alogrithm model的信念。
在回归学术圈后,我在看最近发表的统计论文时,发现这些论文提出的模型和他在做商业咨询时的需求格格不入。我认为虽然data model获得了很大的成功,但是对于这些模型的滥用也导致了很多不靠谱的结论。而因为data model的成功,也导致统计学家对现代统计模型并不感兴趣。
但是在过去的15年中,我发现在远离统计学的另外一个圈子,机器学习,却产生了一种新的统计建模方法,即algorithm model。
在这些新模型上,我们最值得学习和思考的有下面三点:
- Rashomon: the multiplicity of good models;即模型的多样性
- Occam: the conflict between simplicity and accuracy;模型的简洁(可解释性)和准确性之间的矛盾
- Bellman: dimensionality—curse or blessing? 维度灾难
2.3 我在做商业咨询时的经历
我给美国环境保护局和州法院,联邦法院做过项目,也分析过交通部的交通数据
其中主要有下列项目:
- 预测明天的臭氧水平
- 通过雷达信号判断船只的种类
- 通过声呐信号预测舰艇类别
- 判别手发摩斯码
- 预测化合物的毒性
- 预测高速公路拥堵的原因
- 语音识别
- 法庭延迟审判的原因
我会详细描述前两个项目。
2.3.1 预测臭氧水平项目
在60年代的洛杉矶深受臭氧污染困扰。当时建立了三个臭氧质量级别,当达到重度污染时,所有公务员禁止开车上班,学生休学。
臭氧污染的主要来源是汽车尾气。尤其是在早高峰后的两三个小时,伴随着太阳光热,尾气中的化合物经过一系列复杂反应,开始转化成臭氧。当时的臭氧污染预警是在早晨发出的,但是如果能够提前12小时即在前一天的晚上发出,会对人们的出行更有帮助,为了这个目的,环境保护局启动了臭氧预测项目。
洛杉矶的交通状况很有规律,每个工作日的交通状况都差不多,只有很小的差别,所以每日的尾气排出量很好预测。在这种情况下,臭氧水平更多决定于前几日的天气状况。为此,我们建立了一个庞大的数据集,包含上百个空气污染监测站的数据,指标包含每小时的地表温度,湿度和风速,总计450个变量。
所以问题可以描述成,x作为自变量,包含了前n天的n $\times$ 450个变量,y作为因变量,为预测的臭氧水平。我们需要找到f(x)。
我们收集了7年的数据,把前5年作为训练集,后2年作为测试集。使用线性回归模型建模,加入二次项和交互项 ,然后用变量选择去减少自变量。但是最终项目失败了,因为误报率太高。
我现在很后悔当时没有尝试使用algorithm model。
2.3.2 氯项目
环境保护局每年都会对几千种化合物进行取样,并且实验其毒性。在70年代中期,实验的标准流程是先测得化合物的质谱,然后通过质谱推断化合物的结构。
测得质谱很快很便宜,但是从质谱推断化合物结构,即便对于一个训练有素的化学家,也是一个费事的工作。环境保护局并不能承担找来一堆化学家,去分析这几千种化合物的结构。所以环境保护局启动了一个自动通过质谱来分析化合物中是否含氯的项目。
质谱是通过在磁场环境中,用高能离子轰炸化合物测得的。化合物分子会分裂成更小的分子,分子质量越小,其在磁场的作用下越偏离原始轨道,当打到目标区域时,可以通过分布的位置和密度来判断分子的质量的分布。最终就生成了一张分子质量分布图,x轴是分子质量(从1到该化合物的质量),y轴是密度。高点代表此处质量的分子较多,密度为0的点代表没有该分子质量。当时已经测得了30000中化合物的质谱及其结构。
我们想通过化合物的质谱来测得其结构中是否含氯。
即x为质谱,y是其结构是否包含氯。
我们把其中25000中化合物作为训练集,另外5000化合物作为测试集,尝试了线性判别分析,二次判别分析,但都因为feature 维度高而效果不好。这次我没有像臭氧项目一样,我尝试使用了决策树,我仔细研究了质谱中氯的特征(做了一些特征工程),然后训练了1500个decision stump(单层决策树),结果取得了95%的准确率。
2.3.3 这些项目的收获
当我离开商业咨询,回归学术时,我总结了我在做商业咨询项目带来的收获:
目标应该是获得good solution,这才是咨询的价值所在。
在建模之前,要仔细分析数据(live with data)。
不管data model还是algorithm model,能给出good solution的就是好模型。
在测试集上的准确性才是判定模型好坏的准则。
计算机是不可缺少的工具。
2.4 回归学术
我想举个例子来说明对于统计学,学术研究是什么样的。在70年代,又一次我的一个朋友,伯克利大学统计系的一个很有名的教授来找我喝茶,当我跟他描述决策树时,他的第一个问题是,数据的模型(分布)是什么?
在我回归大学后,我开始阅读Annals of Statistics,它是理论统计学最重要的期刊,然后我就蒙逼了。因为每篇文章的开头都是:
假设数据的生成过程符合以下模型... 然后是数学推导和假设检验。
我深深的觉得,在实际应用中使用这些data model,可能会导致不靠谱的结论和政策决策。
2.5 data model的滥用
应用科学的统计学家认为数据建模是统计分析的第一步。统计学家相信,即使在面对一个复杂问题时,也可以通过猜想和仔细分析数据,来对数据进行参数建模。然后进行参数估计,得出结论,走向人生巅峰。
但是,当对数据进行建模时,有以下的问题:
这样得出的结论是根据你设想的data model得出的,而不一定是真正的自然机制。
如果这个设想的data model不靠谱,那结论就是完全错的。
这似然是件很显然的事情,但是却常常被忽略了。
十几年前,对于data model的信任甚至连基本的残差分析都不做的好吗。当时对于data model正确性有着宗教般的信仰,data model就是真理。
2.5.1 举个栗子
我来用一个很有名的例子(好像也不是很有名),假设数据服从以下模型:
$$y=b_0+\sum_1^M b_mx_m+\epsilon$$
其中系数$b_m$是要估计的参数,$\epsilon$符合正态分布。然后我们可以进行参数估计,假设检验,置信区间,以及画出残差图。一切都很完美,尤其对于数学家来说。理论统计学家,工程师都很看重在linear model的情况下,系数的显著性水平,但是几乎没有人关心我们的数据是不是真的是linear model生成的?所有的期刊文章都认为他们能从这些linear model中推断出结论,为什么呢?因为参数的显著性水平在5%的水平上。
拟合度(goodness-of-fit)一般是通过$R^2$计算,越接近0越好。参数越多,一般来说$R^2$]越大。除了看$R^2$以外,并没有什么好方法来验证数据集是由linear model生成的。举个例子,有个十几年前的研究,是由一所著名大学统计系的教授们做的,目的是统计推断出在大学的教员中是否存在薪水上的性别歧视。他们建立了一个数据集,有25个特征,包含发表的文章数量,期刊级别,教学水平,性别等。
他使用线性回归后,最后得出gender系数的显著性水平在5%,这是说明存在性别歧视的强有力的证据。但是这个实验在设计上出现了一些问题,他们得出的显著性水平真的足以回答这个问题吗?这个推断是公平的吗?他们过于focus在model上,而忽略了很多问题。
期刊上的很多文章,使用线性回归模型得出了很多错误的结论,因为他们只看到了5%的显著性水平,而并不知道他们的数据是否真的满足线性回归模型的数据假设。现在,我觉得很多统计学家已经意识到了这种得到结论的方式是不可靠的,是值得质疑的。但在当时,几乎没有统计学家对这样的流程提出过反对意见,他们都被这包装漂亮的童话故事蒙蔽了。尽管到了现在,对于data model的滥用,也很少有公开的批评。其中一位批评这种问题的教授是David Freedman,大名鼎鼎的Statistics教材就是他写的。(另外一本教材里他讲了对LR的批评)
2.5.2 目前数据建模中的问题
目前在统计实践中,判断模型能不能拟合数据是通过$R^2$和残差分析来完成的。几年前我试过模拟一个七维的线性数据,其中带有一些非线性。它可以轻松通过标准的拟合度测试,除非其中的非线性部分非常非常大。最近的研究也说明了这一点,拟合度测试基本上不起什么作用,因为除非是极端的不fit,拟合度测试才会reject。
更进一步,如果model根据数据进行了修修补补,比如删掉某些variable,或者增加一些非线性的多项式项或交互项,那拟合度测试和残差分析就更不适用了。William Cleveland,残差分析的发明人之一,承认超过四维的数据,残差分析并不能测试出其真正的拟合程度,好的残差图也并不能说明数据很fit模型。(因为当维度高了以后,对同样的数据,很多模型对应的残差图都很好)
所以说,通过了拟合度测试,得到了5%显著性水平的系数,仍然可能得出错误的结论。
但是在期刊文章中,作者一般对数据是否真正拟合模型并不关心,更关心自己构造出的精巧的随机模型。
2.5.3 data model的多样性
统计学的目标是从数据中抽丝剥茧,尝试还原数据的生成过程。
data modelling最大的优点就是它用一种比较简单的,可解释的模型来描述input和response variable之间的关系。比如说,逻辑回归常在分类任务中使用,是因为它可以对input进行简单的线性组合,就得到了input是如何影响response的权重,还自带置信区间,这对普通人来说就是神器啊。
假设有两个统计学家,每个人用不同的方法对同一数据集进行建模。每个人都使用拟合度测试,残差分析,并且在这之后都认为他们的模型可以拟合数据集。但是他们最终得出的模型一定是有很大差异的,并且都认为自己的模型真实的还原了的数据生成过程。
McCullah 和 Nelder曾说过:“数据通常可以和很多个模型同时匹配(拟合),统计学家应该注意到这一点,并且承认这一点。” 说的太好了,不同的model,可能都很好,只不过是数据(x->y关系)不同角度的描述。所以并不能说其中某个模型就好过其它的模型。
从拟合度的角度来看,对一个四维以上的数据,可能有非常多的model都fit这个数据,所以并不能通过拟合度测试来说明哪个model更好,因为他们都很好。可惜的是,只有很少的统计学家清楚这一点。Mountain和Hsiao说过:很难构造出一个完整的model,这个完整的model包含了所有的备选model。
2.5.4 预测准确性
评价一个model的好坏,显而易见的方法就是把x放到这个model里,看产生的y和真实的y的区别,越小代表model越好。对于data model来说就是,使用data进行model fitting,然后用预测准确率来衡量该model的好坏。
预测都是不完美的。因为有很多未统计的变量,带来了noise。
McCullagh and Nelder 在他们的《Generalized linear model》一书中提到:在一开始,人们似乎认为好的model就是能很好的fit data的model,然后他们发现参数的数量可能会导致fit的程度不同,所以这不是一个好的度量方式。这是对的,因为过多的参数可能会引起overfitting,其准确性是biased。但是可以有方法去掉这部分bias,为了得到无偏一些的估计,可以使用cross validation。如果你的数据集很大,也可以直接用test set的方式。
Mosteller 和 Tukey 也是早期推广cross-validation的学者,他们写到:“cross validation是一种非常自然的模型度量方法”。
但是Journal of the American Statistical Association上的文章却很少使用cross validation,对于我和Mosteller, Tukey来说,cross validation是很自然的,但是对于其它学者来说却不是这样。但我相信,预测准确率会是以后评价模型的标准,会被广大学者接受,就像预测准确率在现在的机器学习领域的地位一样,已经被广泛使用。
2.6 data model的局限
学术界对于data model的坚持,导致了统计模型在判别分析,线性回归,逻辑回归模型上的停滞不前,没有人真的相信多元数据是多元高斯分布的,但是在多元统计分析的教科书中,但是这类模型却占据了相当大的篇幅。
当数据是从复杂系统,涉及到未知的物理,化学或生物过程中采集的时,那假定这个过程符合某个统计学家挑选的参数模型便是有点naive了,这肯定会导致不靠谱的结论,但是它偏偏还能通过拟合度测试和残差分析。一般来说,把简单的模型套在复杂系统上,一定会丢失信息量的和准确性的。
有句古语叫做:如果你有个锤子,那么所有东西都看上去像钉子。
在如今的统计学中,很多问题现在并不像是钉子了。我猜想当越来越复杂的data model越多出现时,比如贝叶斯加上马尔可夫蒙特卡洛,那么离捅开这层窗户纸就不远了。因为data model越来越复杂,那么当data model最大的优点:简单和可解释性丢掉时,data model就彻底没啥优点了。
把data限制在assuming model中,也限制了统计学家解决问题的能力圈。解决一个数据问题的最好方法可能是data model,但也可能是algorithm model。为了解决更多的问题,我们需要更好的model。
如果统计学还是固执于data model,那么很有可能在最新,最有趣,最有挑战性的这些复杂问题中,统计学家会掉队,而是非统计学科的人却抓住了机遇,最后发现了解决这些问题的方法。
2.7 algorithm model
algorithm model,在很早以前就在很多统计学家的书中,以其它名字的形式出现过了。但是这些统计学家是很少的,并且在期刊中也很少见到。algorithm model的大本营在统计学之外,在一个叫机器学习的圈子中。
2.7.1 一个崭新的学术圈子
在80年代中期,2个新的统计模型开始兴起:神经网络和决策树。他们的目标就是预测准确性。这个圈子主要是由年轻的计算机学家,物理学家和工程师,和一小拨统计学家组成。他们用这些新模型,来处理一些显然不适用于data model的复杂预测问题。比如语音识别,图像识别,非线性时间序列预测,手写识别,金融预测等。
这个圈子的研究领域涉及很广,很多问题是统计学家过去战斗过的问题。
2.7.2 algorithm model理论
在这个圈子里,基本上不使用data model。
这个圈子里认为,对于复杂系统或自然过程来说,其内部工作机制是复杂的,未知的,神秘的。我们的目的是找到从x生成y的f(x)映射。
这个圈子把研究的焦点从对数据进行建模,转向到了算法特性方向。他们对数据的唯一假设是数据是独立同分布的,且来源于一个未知的多元分布。
统计学界也有类似的研究,但是属于非主流和少数派。
Vladimir Vapnik创造了一套根据分类算法capacity来计算generalization error上界,从而发展出了svm算法。svm被证明比神经网络有更好的预测准确性。
我的论文《Some infinity theory for tree ensembles》尝试分析了树集成方法的工作过程。现在已经有了boosting方法,但是对于它为什么work,还没有很好的理论解释。
2.7.3 最近的启发
预测准确性和algorithm model在80年代中期的兴起,在机器学习界产生了很大影响。在过去5年中,有很多令人兴奋的进展,从这些进展中我学到了下面三件事情:
Rashomon: the multiplicity of good models;即模型的多样性 Occam: the conflict between simplicity and accuracy;模型的简洁(可解释性)和准确性之间的矛盾 Bellman: dimensionality—curse or blessing? 维度灾难
2.8 罗生门和模型多样性
罗生门是一部日本电影,讲述了四个人,从对各自有利的视角, 对一宗杀人案不同的供述。在法庭上,他们都的故事结局相同,但是过程却大不相同。
我所称作的罗生门效应,指的是通常会有很多的f(x),可以得到同样的error rate。最容易理解的例子是线性回归中的特征选择。假如说有30个特征,我们最终像选出其中5个,这有14000种组合方式,通常我们用RSS或者test error来选择。但是我们可以发现,在RSS 最小的前1%种,可能有很多模型是5个feature;或者在test error最小的1%个模型种,可能存在多个模型。
比如可能是这样的:
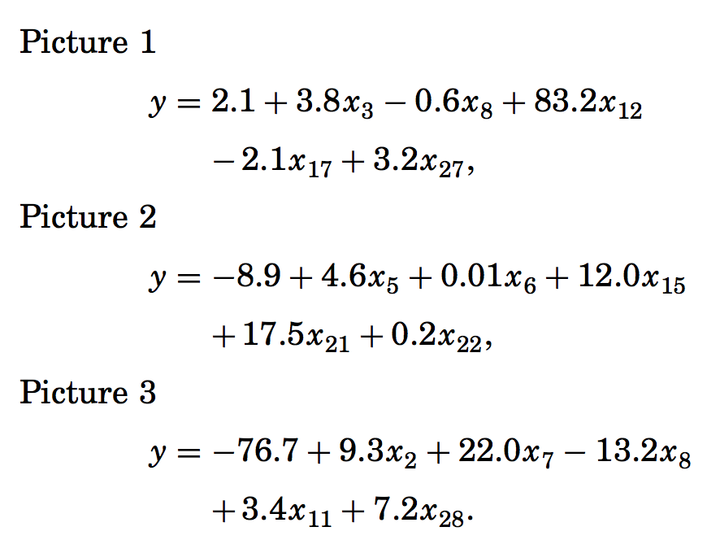
哪个是最好的模型呢?每个模型讲的故事都大不相同,但是最终的error rate却相差无几。
罗生门效应同样出现在决策树和神经网络中。我曾经试验过,如果把training set稍微做点手脚,比如说随机去掉其中2%-3%的数据,我们可以得出和原模型大不相同的训练模型,而error rate却差不多。在神经网络上,通过对参数进行初始化时的细微调整,也可以得出不同的模型。
这种效应和我提出的概念instability紧密相连,即对于同样的training error或test error,会有很多的模型同时存在。training set的小手脚就可以从一个模型得到另外一个模型,两个模型的error近似,但是模型本身却大不相同。
比如对于逻辑回归来说,一般都会进行特征选择,这就会带来instablity。
比如有15个feature,但我们只想要4个feature,那么对training set动一点手脚就可能得到完全不同的模型,也就是得到完全不同的对各个variable重要性的解释。
所以就有了aggregating一堆model的想法。比如有一篇论文提到在15个feature,选出4个variable的例子中,使用bagged model会比使用单一model得到正确率的很大提升。
2.9 奥卡姆剃刀: 模型简洁性 vs 模型正确率
奥卡姆剃刀原则,通常说成是:模型越简单越好。但不幸的是,在预测时,简洁性(simplicity),或者说可解释性(interpretability),是和预测正确率(accuracy)相矛盾的。比如说,线性回归可解释性很好,但是预测正确率通常要比神经网络低。
在可解释性上,决策树是A+的。在70年代我参与过一个项目,分析州法庭刑事案件的延误审判情况,被告有提出尽快审判的权利。但是在很多州,并没有审判加速的情况发生。我访问了很多州,最后决定在Colorado州进行分析,因为那里保存了最完整的审判材料。
从开始审判到最终判决的时间作为y,其它变量作为x。使用决策树进行建模,当我把这个模型拿给州最高法院的法官去看时,里边有一个分支,是N街区的罪犯相比其它罪犯有很大的延迟,有个法官说,我就知道这个负责N街区的法官总是拖拖拉拉的。
决策树的可解释性很高,可以打A+,但是它的预测正确性只能说一般般,也就B吧。
2.9.1 森林
森林是指由很多树组成的classifier,比如50个,100个树这个样子。然后在预测时,采取投票的方式来决定。构造森林的方法多是对training set动动手脚,比如随机去掉2%的数据,然后训练颗树,再从头开始随机去掉2%数据,训练颗树。。。
一些有名的方法是bagging,boosting,arching和addictive logistic regression。我最喜欢的方法是random forests。
2.9.2 随机森林 vs 单棵树
我们来比较下单颗决策树(CART)和随机森林的性能。
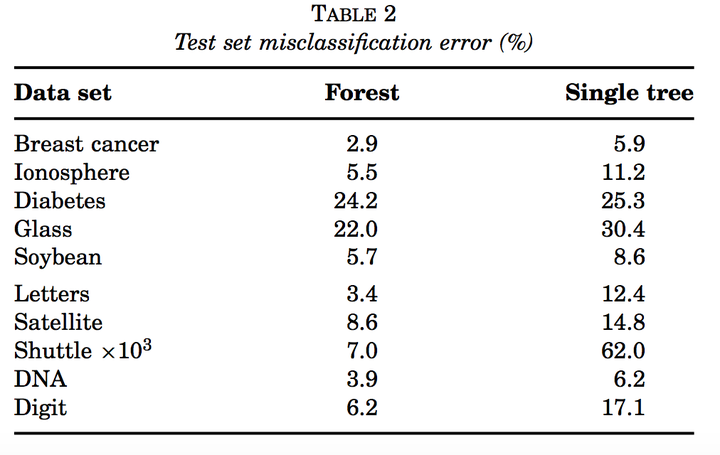
从上图可以看到,随即森林比单颗树不是好一点半点啊。在regression任务中,MSE的减少也和上图类似,减少1/2到2/3左右。
2.9.3 随机森林是A+ Predictor
在Statlog Project中,研究人员比较了18种分类器,包括神经网络,CART,线性和二次判别分析,最近邻等。随进森林是表现最好的分类器。
2.9.4 奥卡姆困境
所以森林可以说是A+预测器,但是却很难解释它是如何进行预测的。所以在可解释性上,只能给它打个F。
这就是奥卡姆困境:预测准确性通常需要复杂的模型。简单和可解释性的模型不能给出很好的预测。
虽然使用复杂模型时不好解释有点让人不爽,但是我们的目标是预测准确性!在预测准确的前提下,去理解其背后的原理,这应该是我们研究的方法。
2.10 Bellman和维度灾难
这一小节的标题是Richard Bellman的名句,"The curse of dimensionality".
在过去的几十年种,预测前的第一步就是降维,避免维度灾难。如果有过多的特征,那么首先要筛选出能表征绝大部分信息量的特征,进行降维。在线性回归,逻辑回归的实践中,一般都建议先进性特征选择。一般认为高维是危险的,比如在一本讲模式识别的书里说:特征的数量一定要相对少。但是最近的研究表明,维度不一定是curse,也有可能是blessing。
2.10.1 反其道而行之
降维减少了可用的信息量。特征越多,信息量越大。所以,让我们来试试升维!
比如我们增加很多多项式项和交互项。加到可能有上千个feature。那每个feature都包含了一些信息,问题是如何从中抽取出有用的信息呢?有两个这方面的研究:Shape Recognition Forest和Support Vector Machine。
2.10.2 Shape Recognition Forest
在1992年,国家标准与技术研究所举办了一场手写数字识别的比赛。数据集收集了2000人的223000个手写数字。比赛引起了很大关注,来自各地的参赛者基本把当时存在的模型试了个遍。
最后胜出的是使用树和森林来构造的模型,达到了测试机上0.7%的错误率。
2.10.3 Support Vector Machine
在支持向量机中,最优超平面的定义是和支持向量间的距离最大的超平面。
Vapnik证明了,最优超平面可以得到最小的generalization error。
在二分类任务中,通常并不是线性可分的。但是,通过增加多项式项和交互项来升维,升的维度越高,则越有可能达到线性可分。但不是升的越高越好,如果太高,则generalization error也可能很大。
Vapid给出了generalization error的bound:
Ex(GE) ≤ Ex(number of support vectors)/N − 1,其中N是sample size
随着维度升高,support vector的数量也会增加,如果这个数量太大,那么generalization error会很高。如果不能用较少的support vector来实现线性可分,那么可以定义soft threshold来处理。
SVM也可以做回归,SVM是一个绝妙的想法,有着出色的表现,赞。
2.11 黑盒中的信息
奥卡姆困境说预测性最好的模型也最不好解释。
自然过程是黑盒的,我们的模型也是黑盒的,所以我们目前面临两个黑盒,只是我们的黑盒要比自然黑盒稍微好解释一些。我一个生物统计学家朋友告诉我,医生可以解释逻辑回归的结果,但是不能解释一个50棵树组合在一起的黑盒怪物。在预测正确性和可解释性上,他们选择可解释性。
但是是不是我们问错了问题?我们只能从正确性和解释性上来权衡吗?
模型的目标是获得x和y之间关系的信息,可解释性只是获得这种信息的一种方式。所以说目标并不是可解释性,而是information。
下面的三个例子说明了这一点。
第一个例子说明随机森林可以比逻辑回归给出更可靠的特征重要性的信息。
第二个例子说明随即森林可以给出逻辑回归不能给出的有趣信息。
2.11.1 例子1: 特征选择
这是一个判断肝炎患者最终存活的数据集,有155个患者,19个特征。
最初分析这个数据集的是Peter Gregory,它分析出其中最重要的4个featue是6,12,14,19.
Diaconis 和 Efron 则从数据集上抽样出500个子数据集,分别在这500个数据集上进行特征选择,然后发现,有60%的数据集选出的特征和Peter Gregory选出的不一样。
2.11.1.1 逻辑回归
逻辑回归在这个数据集上的错误率是17.4%。
从下图可以看出,7和11是最重要的feature,只使用这两个feature,得到的错误率是22.9%。
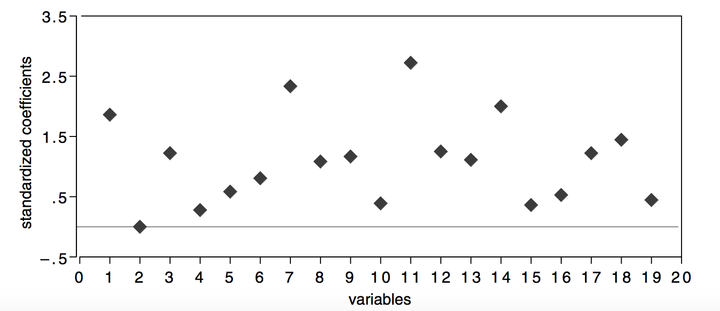
2.11.1.2 随机森林
随机森林在这个数据集上的错误率是12.3%,相比LR,减少了30%。
在随机森林中,用去掉某个特征,然后测试错误率增加了多少来衡量该特征的重要性。
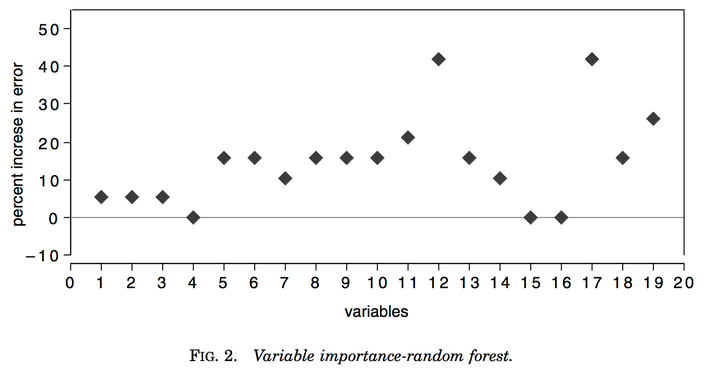
下图是随即森林认为的最重要的特征,第12,17是最重要的两个特征。单独使用其中一个特征可以得到14.3%的错误率,两者同时使用时错误率没有降低(可以推断出两者是高相关的)。所以我们可以推断,在这个问题上,基本上所有的信息都来源于12,或17特征中的一个。
但是可以看出,随即森林选出的12或17,并没有出现在LR选出的最重要的特征当中。出于好奇,我用12和17分别做逻辑回归,错误率分别是15.7%和19.3%,竟然比上面提到的17.4%要好。
为什么呢?
因为12和17是高相关的,引起了共线性问题,这导致了在特征选择时,如果其中一个权重高,那么另外一个的权重则很低。当选用500个子数据集在这些上做LR模型时,只有一半的模型12权重高,也只有一半的模型17权重高,各自50%,相当于他们真实权重都打了个5折。所以上面在做LR的时候并没有选到最好的特征,错误率很高。
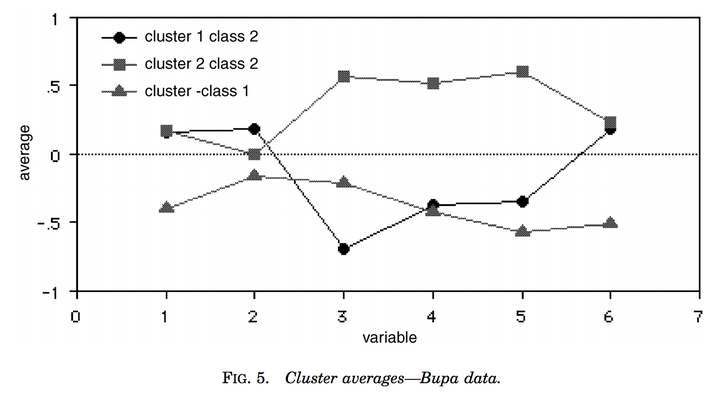
2.11.2 例子2:医学数据聚类
在一个肝功能分类数据集上,随机森林还可以给出聚类信息。可以看到class 2分成了2个cluster。
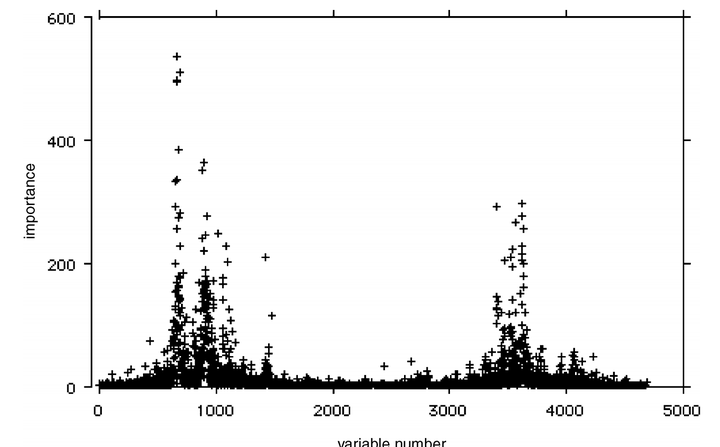
2.11.3 例子3:DNA微阵列(基因芯片)
淋巴瘤数据集,4600个特征。
结果错误率很低,特征重要性和其它算法做出来的一致,但有更清晰的细节。
2.11.4 三个例子的总结
这三个例子说明algorithm model可以提供更多的信息。
随机森林可以发现其它模型发现不了的信息,比如例子2.
不像统计学,机器学习认为特征越多越好,特征越多信息量越大。(像svm一样)
随机森林可以避免overfitting,在第三个例子中,在没有做特征选择的情况下,随机森林给出了很低的错误率。
所以我们在回顾下作者提出的三个问题:
- Rashomon: the multiplicity of good models;即模型的多样性
- Occam: the conflict between simplicity and accuracy;模型的简洁(可解释性)和准确性之间的矛盾
- Bellman: dimensionality—curse or blessing? 维度灾难
随机森林和svm,基本上就是颠覆了原来人们对这三个方面的理解:
- 原来人们认为model应该时唯一的,但随机森林说应该是不同角度的model的组合。
- 原来人们认为简洁性和准确性是矛盾的,但实际上随机森林可以提供更可靠和更多的信息,简洁性带来的可能是错误的信息
- 原来人们认为维度是灾难,但是随机森林和svm认为维度是blessing。
2.12 总结
我并不排斥data model,相反我觉得在一些问题上,data model可以给出很好的结论。
但是,过度的使用data model,是明显错误的。比如Dempster在1998年的文章中说他并需要仔细了解数据就可以对数据进行建模。
我相信algorithm model会是未来的趋势,是个创新百出的领域,我们等着看吧!
data model可以认为是传统统计模型,algorithm model则是现代统计模型。
对于简单问题或简单的系统建模,data model很适用,但是对于一些复杂的现代问题,比如图像识别,语音识别,algorithm model比如神经网络,随机森林更适用。
未来的机会一定在于处理复杂世界中的复杂问题,所以一定要拥抱algorithom model,尤其是深度学习。