1 优化和深度学习
优化算法的目标是减少训练误差,追求损失最小化
深度学习的目标是减少泛化误差,寻找合适的模型
由于深度学习的优化算法一般是围绕误差传播和梯度展开的,因此围绕当梯度消失或值接近0时,会极大地干扰到深度学习的优化过程,其中常见的三种情况是:
- 局部最优值:当数值解迭代至局部最优解时,梯度会接近0,最终使得模型收敛到一个次优的结果,通过在训练过程中添加一定程度的噪声(比如小批次梯度下降法)能改善此问题
- 鞍点:鞍点所在位置的梯度也会是0,因此损失函数一般会尽量设计为凸函数以规避此问题
- 梯度消失:构建深层网络时,非常容易出现梯度消失/爆炸的问题。改善梯度消失问题的技巧很多,比如残差连接、ReLU激活函数等
一般来说,梯度下降法在神经网络中找到的都是局部最优解,而不是全局最优解。
2 凸性
凸集(convex set):凸集$\chi$内任意两点间连线,线段也在凸集$\chi$内
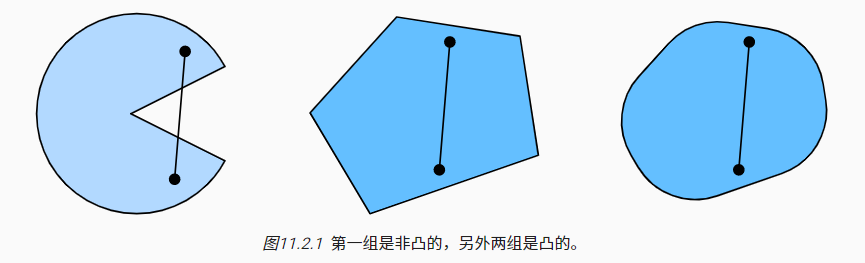
凸集的性质:
- 两个凸集的交集也是凸集,并集可能是非凸(nonconvex)的
凸函数(convex function):凸集经过凸函数映射后,依然是凸集
凸函数$f$满足詹森不等式(Jensen’s inequality): $$E_x[f(x)]\geq f(E_x[x])$$
凸函数的性质:
- 凸函数的局部极小值也是全局极小值
- 凸函数的下水平集(below sets)是凸的,下水平集定义:
$$S_b:={x|x\in \chi \ and \ f(x)\leq b }$$
- $f''>0$可以推导出$f$是凸函数,此结论在多维情况下依然成立
对于带约束的最优化问题,可以考虑使用拉格朗日乘子法
当目标函数是凸函数时,随机下降法能找到全局最优解。不过本书中提及的MLP、CNN、RNN、Transformer都是非凸的,常见的凸函数算法有线性回归和softmax回归
3 梯度下降
梯度下降法:梯度下降法族
牛顿迭代法:拟牛顿类算法
4 随机梯度下降法
随机梯度下降:4 随机(Stochastic )梯度下降法
关于随机梯度下降法原书中还包括一些可选内容:面对凸函数的收敛性分析
5 小批量随机梯度下降
小批量随机梯度下降:5 小批次(mini-batch)梯度下降法
向量化使代码更加高效:
- 发挥服务器的并行处理能力,提高计算效率
- 减少内存和缓存中的存取开销(更充分的利用带宽,降低延迟)
- 减少深度学习框架的额外开销(多次命令合并为了一个命令)
6 动量法
带有动量的梯度下降法:6 带有动量(Momentum)的梯度下降法
7 AdaGrad算法
自适应梯度下降法:7 自适应梯度下降(AdaGrad)算法
8 RMSProp算法
RMSProp算法:8 RMSProp算法
9 Adadelta算法
Adadelta算法:9 AdaDelta算法
10 Adam算法
Adam算法:10 Adam算法
两个改进方向:
- 修正基于平方和的历史梯度累积更新,比如Yogi更新
- 使用较多批次的数据进行动量的初始化,提高算法的启动速度
11 学习率调度器
对学习速率进行自定义的衰减
- 常见的单因子策略包括:多项式衰减、分段常数式衰减、乘法衰减
- 一般来说,策略中的学习速率都会随着迭代过程逐渐衰减(注意设定合理的下界)
- 余弦调度器:在迭代的后期使用很小的学习速率来慢慢地改进模型
- 预热(warm-up):先通过较小的学习速率对参数的初始化进行合理修正