大模型幻觉的常见三种情况:
- LLM 模型输出内容和输入不一致(驴唇不对马嘴)
- LLM 模型输出内容中包含与上下文不一致的内容(自我矛盾)
- LLM 模型输出内容和世界知识/训练注入的知识不一致
1 幻觉四象限

- 右上是最优情况(知之为知之),左下是次优情况(不知为不知)
- 左上是最差情况,右下是次差的情况;二者需要尽量转移到更优的象限内
2 模型知道,模型认为自己不知道
模型具有正确的内部知识,但模型输出的内容存在错误
如何判断“模型知道,模型认为自己不知道”
- 同一知识点的不同题型,模型存在分歧;比如 G-D gap,就是指模型在针对同一知识点进行生成式任务(比如问答题)与判别式任务(比如选择题)容易出现不一致的情况
- 通过提示让模型能实现自我纠正,这说明模型其实是知道这种知识的
- 重复输出结果,模型可能给出正确答案(可能是模型的 top-p 输出采样策略导致的)
hallucination snowballing 幻觉雪球效应,这是导致 LLM 模型出现幻觉的一种重要原因;即 LLM 在缺乏自我纠正的情况,为了自圆其说而导致幻觉和虚假信息放大的情况
改进策略:
- 干涉模型生成时的内容状态,比如 ITI(inference-time intervention) 方法
- 优化解码方法,比如层对比解码(Decoding by Contrasting Layers, DoLa)
- 让模型自己判断生成内容的准确性(Self-check);比如提示优化、通过多次生成的一致性来判断是否存在幻觉、对特定生成任务与客观结果(比如引用文章与作者)进行一致性对比
2.1 ITI - 推理干预
原论文借用“探针(probe)”来挖掘不同的层的注意力头精度,“探针“的本质其实就是训练分类器以区分特定的输入和输出;在本文中主要用于衡量每个注意力头与幻觉/错误输出的关系:
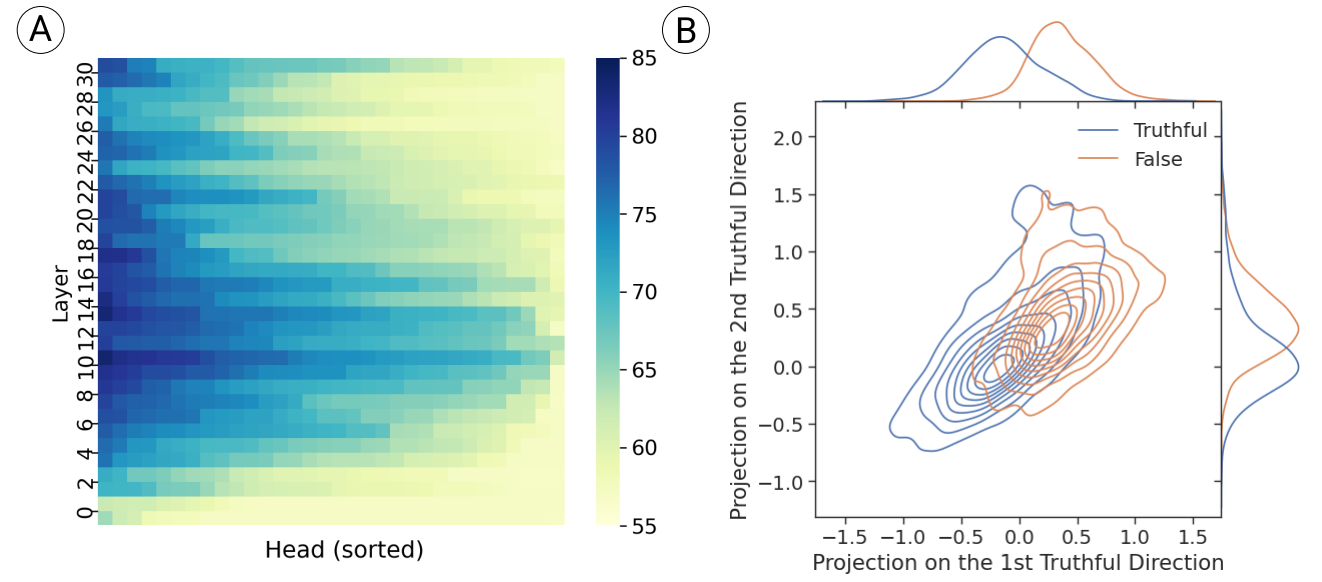
- 图 A 表示不同层的注意力头的精度(描述了对模型区分幻觉的贡献度);按层数高低由上到下排序,按精度高低由左到右排序(基线精度是50%,相当于随机乱猜)
- 图 A 显示,每一层都会有几个注意力头具有较高的精度;中部层具有最多的高精度注意力头(说明幻觉的区分主要依赖于模型的中层参数);几乎所有注意力头的精度都在50%以上
- 图 B 是针对第 14 层第 18 个注意力头的进行了”真实/虚假”几何分布的可视化,该注意力头实现了 83.3%的最高精度,其可视化来自两个“探针”的模型参数的几何映射;第二“探针”使用了同样的训练方法,但额外增加约束限制:“探针”参数与第一维度正交
得益于以上的结论,论文提出了 ITI(inference-time intervention) 方法
- 该方法仅干涉每层的 Top-K 个注意力头(因为大部分注意力头与输出的真实性无关)
- 该方法的核心在于对注意力头的输出进行偏移(从”虚假”分布向“真实”分布偏移)
- 偏移方向既可以考虑“探针”学习到的参数向量,也可以考虑使用两个分布的均值差异
$$x_{l+1}=x_l+\sum_{h=1}^HQ_l^h\left({Attention}_l^h(P_l^hx_l)+\alpha\sigma_l^h\theta_l^h\right).$$
- 其中$\alpha$描述了偏移干预的强度;$\sigma$表示激活值的标准差(基于训练集和验证集的估计)
- $\theta$为“探针”模型的参数(归一化后),对于不需要干预的注意力头来说$\theta$是零向量
效果评估(TruthfulQA 数据集):

- 有一定改善,尤其是 Baseline (LLaMA);但是对于提示微调后的模型改善幅度较少
- 针对特定模型或特定领域的问题,可能存在较大的精度改善(至少不会下降)
2.2 DoLa - 层对比解码
本文的 DoLa 方法启发过程:
- 较早的层编码了"低级"信息(词性),而后面的层中包含更加“高级”的信息
- 通过强调较高层中的知识并淡化低层中的知识,从而减少 LLM 的幻觉
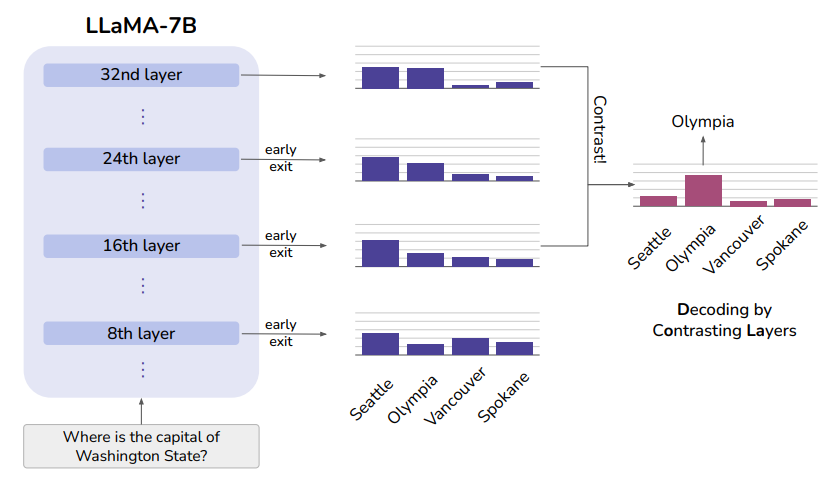
- 针对提问:华盛顿州的首府是哪里(where is the capital of Washington State)?
- “西雅图(Seattle)”这一答案在模型的不同层呈现较为相似的输出概率
- 而正确答案“奥林匹斯(Olympia)”则随着模型的层数加深而增加了输出概率
DoLa 方法细节:
- 得益于目前普遍存在从残差连接技巧,目前的 LLM 基本都支持
early exit,即使用中间层的 hidden states 作为最终的 hidden states 应用到模型的输出中 - DoLa 方法会针对中间层并运用
early exit技巧,之后使用 Jensen-Shannon 散度筛选出与最终层输出差异最大的中间层(记为$M$) $$M=\arg\max_{j\in\mathcal{J}}\mathrm{JSD}\big(q_N(\cdot\mid x_{<t})||q_j(\cdot\mid x_{<t})\big),$$ - 上式中,$J$表示对层分桶后的桶数(减少遍历中间层的计算成本);$q_N$表示最终层输出,$q_j$表示中间层通过
early exit得到的输出;$M$是筛选得到中间层数 - 最终 DoLa 方法的原则是最大化最终层输出的同时,淡化$M$层的输出:
$$\begin{gathered} \mathcal{F}\big(q_{N}(x_{t}),q_{M}(x_{t})\big) =\begin{cases}\log\frac{q_N(x_t)}{q_M(x_t)},&\text{ if }x_t\in\mathcal{V}_\text{head }\left(x_t|x_{<t}\right), \\-\infty,&\text{ otherwise.}\end{cases} \\
\hat{p}(x_{t}) =\text{softmax}\big(\mathcal{F}\big(q_N(x_t),q_M(x_t)\big)\big) \\
\mathcal{V}_\text{head}\left(x_t|x_{<t}\right)= \left\{x_t\in\mathcal{X}:q_N(x_t)\geq\alpha\max_wq_N(w)\right}. \end{gathered}$$
- 其中集合$\mathcal{V}_\text{head}$主要用于筛除掉过早层预测精度过低的情况
此外,由于实验过程中发现 DoLa 方法在CoT推理较长序列的过程中,倾向于生成重复的句子;因此本文还针对这一情况单独构建了避免重复生成的惩罚项
效果评估:
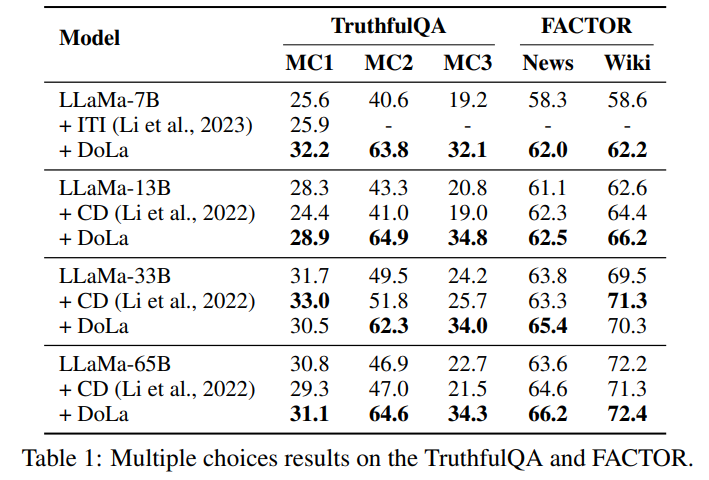
3 模型不知道,模型认为自己知道
一本正经的胡说八道或生成结果的一致性很低
为什么会出现“模型不知道,模型认为自己知道”这种情况:
- 缺乏内部知识或知识探测方法
- 模型过度自信(over-confidence)
- 强化学习的奖励机制(偏好附和人类)
- 微调导致的不对齐问题(在缺乏知识的问题上微调等于鼓励幻觉)
观点 4 引用自 openA I的 John Schulman 的演讲
解决方法:
- 让模型知道:工具增强(RAG),知识注入
- 让模型诚实:提示工程(prompt),诚实性微调(Honesty-oriented finetune)