中文标题:将宏观-行业-微观财务指标耦合,以降低股票表示的不确定性。
英文标题:Coupling Macro-Sector-Micro Financial Indicators for Learning Stock Representations with Less Uncertainty
发布平台:AAAI
Proceedings of the AAAI Conference on Artificial Intelligence
发布日期:2021-05-18
引用量(非实时):23
DOI:10.1609/aaai.v35i5.16568
作者:Guifeng Wang, Longbing Cao, Hongke Zhao, Qi Liu, Enhong Chen
文章类型:journalArticle
品读时间:2024-01-27 9:47
1 文章萃取
1.1 核心观点
本文引入了一种无监督的 Copula 增强对比预测编码(Co-CPC)模型来表示异质宏观经济变量与股票之间的耦合和影响,在保留了这些变量各自的特征并抑制了由于它们的错位而引起的噪声,从而同时处理它们的异质性、相互作用和影响,为处理股价变动任务的数据不确定性提供了新的视角。
1.2 综合评价
- 通过训练集和验证集的对比,本文提出的方法能显著改善股票表示的鲁棒性
- 本文的方法可以拓展到其他时序预测任务中,很方便扩展模型融入额外信息
- 整体的结构较为复杂,训练难度较大;缺少消融实验验证不同部件的贡献度
1.3 主观评分:⭐⭐⭐⭐⭐
2 精读笔记
2.1 背景知识
微观 vs 宏观
- 微观指标:更新速度快,与股价波动相关性更强,善于捕捉短期、局部的影响关系
- 宏观指标:在经济学中,汇率、利率、工业生产和通货膨胀等基本宏观经济变量被认为与股票价格相关或影响股票价格
- 一种简单的方法是直接将宏观变量作为特征与微观变量拼接,但预测性能不显着;因为该方法对宏微观变量耦合(称为数据不确定性)的建模能力相对有限
- 不同宏观经济指标是异质且不一致的,它们具有不同的分布,并随着时间的推移而演变宏观层面;宏观指标和微观指标虽然都是连续的,但在数值、粒度、区间和分布等方面彼此不一致
为了实现更好的预测性能,本文考虑将编码器和解码器模块的学习过程分开,因为基于预测损失直接学习的编码器无法为解码器(预测器)学习更好的股票表示
本文的模型遵循编码器-解码器框架,但每个部分都是单独训练的。特别的是,编码器功能是在不基于特定股票未来标签的情况下学习的,以减轻未来随机数据的干扰
n 维 Copula 函数 $C:[0,1]^n\rightarrow[0,1]$
- 是一组针对边际随机变量 $\mathbf{u}=(\mu_1,...,\mu_n)$ 的联合累积分布函数(CDF)
- Sklar 定理指出每个多元 CDF 都可以分解为其边际分布 $F$ 和唯一的 copula 函数 $C$
$$ F(\mathbf{u})=C(F_1(u_1),...,F_n(u_n)) $$
本文使用 Copula 函数主要有两个原因:
- Sklar 定理的分解方式确保了单变量边际分布和依赖关系的相对独立性,这样就可以灵活地扩展 copula 方法来学习信息丢失和错位时的边缘分布
- 当针对变量进行变换时(比如转到隐空间),只要转化函数是严格递增的(strictly increasing),那变量的依赖关系在变换后也能保持不变
Copula 非常适合对异质宏观经济变量与一个特定股票行业之间的关系进行建模
2.2 算法细节
模块 1:宏观行业环境学习
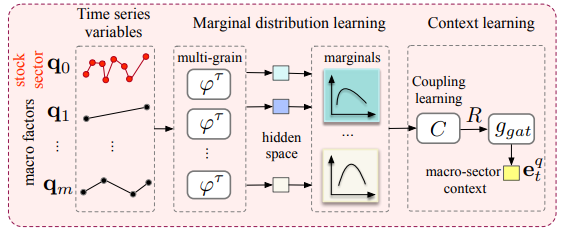
- 为了处理变量之间的异质性和错位,每个观察序列都经过多粒度 LSTM 被映射到隐藏状态 $\mathbf{h}_{i,t}$;其中 $q_0$ 表示股票价格时序,$q_1,...,q_m$ 表示不同类型的连续宏观变量:
$$ \begin{aligned}\mathbf{h}_{i,t}^\tau&=\varphi^\tau(\mathbf{h}_{i,t-1}^\tau,q_{i,t\tau},\mathbf{p}_t;\theta_h),\quad i=0,1,...,m \\\mathbf{p}_t&=Lookup(\kappa(t))\end{aligned} $$
$\varphi^\tau$ 表示多粒度 LSTM,其中 $\tau$ 表示时间间隔,时间间隔相同的观察序列共享 LSTM 的参数;$\kappa(t)$ 表示时间,比如一周中的某一天和一年中的某一天;$\mathbf{p}_t$ 表示时间的嵌入表示
- 假设这些观测值满足高斯分布,则每个时间序列都会唯一地根据其隐藏状态 $h_{i,t}^\tau$ (确保不同边际分布之间的独立性)来构建边际分布 $\hat{F}_i$:均值为 $\mu_{i,t}=\mathbf{w}{\mu}^{\top}\mathbf{h}\{i,t}^{\tau}$,方差为 $\sigma_{i,t}=\mathbf{w}{\sigma}^{\top}\mathbf{h}\{i,t}^{\tau}$
- 使用一个 copula 函数将所有边际分布聚集在一起,以学习协方差矩阵为 R 的联合分布 $C$
$$ C(\cdot)=\Phi_\mathbf{R}(\Phi^{-1}(F_0(q_0)),...,\Phi^{-1}(F_m(q_m))) $$
其中 $\Phi^{-1}$ 是标准正态分布的逆累积分布函数;$\Phi_\mathbf{R}$ 是均值向量为零,协方差矩阵为 $R$ 的多元正态分布的联合累积分布函数;在后文中,将使用 $\hat{F}_i$ 来近似表示边际分布 $F_i$
- 学习方程中协方差矩阵 R 的损失可以写成最大似然估计(MLE)的形式:
$$ \begin{aligned}\mathcal{L}_C&=-\sum_{i=0}^m \left\{\log\Phi_\mathbf{R}(\mathbf{u}_0,...,\mathbf{u}_m)+\sum_t\log\hat{f}_i(\tilde{q}_{i,t})\right} \\\mathbf{u}_i&=[\Phi^{-1}(\hat{F}_i(\tilde{q}_{i,1};\beta_i)),...,\Phi^{-1}(\hat{F}_i(\tilde{q}_{i,t\tau};\beta_i)),...]\end{aligned} $$
其中 $\hat{f}_i$ 表示边际分布的概率密度估计;$\tilde{q}_{i,t\tau}$ 表示第 $i$ 个变量在序列中的排名,排名确保了变量转化前后的依赖关系不变;$\mathbf{u}_i$ 表示逆变换后的第 $i$ 个时间序列的表示
训练过程中,函数 $\Phi_\mathbf{R}$ 需要计算协方差矩阵 $R$ 的逆矩阵,这可能会导致数值不稳定的问题;本文使用 Wen and Torkkola 2019年发表的一篇论文 中提出的方法来强制 R 的稳定参数化
- 最后,本文设计了一个门函数 $g$ 来整合各种因素(宏观因素/股票板块等)对特定股票的作用,并最终形成特定的宏观行业环境上下文表示 $e_t^q$:
$$ \begin{aligned}\boldsymbol{\alpha}=g_{gat}(\mathbf{R})&=Sigmoid(\mathbf{w}_R\mathbf{R}+\mathbf{b}_R) \\\mathbf{e}_t^q&=\sum_{i=0}^m\alpha_i\mathbf{h}_{i,t}^\tau \end{aligned} $$
模块 2:股票表示学习
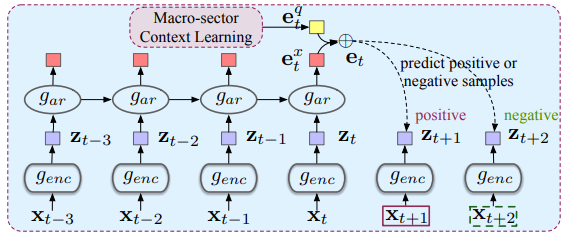
- 首先使用非线性编码器 $g_{enc}$ 将输入特征 $x_t$ 转化为潜在表示 $z_t$,然后使用自回归模型(比如 GRU)对隐藏空间中的所有 $z$ 进行时序信息聚合,得到股票的表示 $e_t^x=g_{ar}(z_{\leq t})$
- 使用多层感知机(MLP)将宏微观的编码信息进行连接:$e_t=MLP([e_t^q,e_t^x])$
- 定义函数 $f_k$ 来描述最终编码信息和未来特征之间互信息:
$$ f_k(\mathbf{x}_{t+k},\mathbf{e}_t)\propto\frac{p(\mathbf{x}_{t+k}|\mathbf{e}_t)}{p(\mathbf{x}_{t+k})} $$
股票表示学习模块主要借鉴 CPC(Contrastive Predictive Coding)的无监督学习方法,先对输入特征进行编码,然后尝试预测未来的编码。预测目标是同一序列中的未来编码和当前编码尽可能接近,而不同序列中的编码尽可能远离(从而挖掘序列本身的内在联系)
- 借鉴 CPC 中的噪声对比估计 (NCE) 技术,定义该模块的损失函数:
$$ \mathcal{L}_N=-\mathbb{E}_\mathbf{X}\Bigg[\log\frac{f_k(\mathbf{x}_{t+k},\mathbf{e}_t)}{\sum_{x_j\in\mathbf{X}}f_k(\mathbf{x}_j,\mathbf{e}_t)}\Bigg] $$
组合以上两个模块,最终模型的损失函数可表示如下: $$ \mathcal{L}=\frac{1}{2\gamma_{1}^{2}}\mathcal{L}_{C}+\frac{1}{2\gamma_{2}^{2}}\mathcal{L}_{N}+\log\gamma_{1}\gamma_{2} $$
- 其中 $\gamma_1$ 和 $\gamma_2$ 是平衡两种损失的超参数
以上模块主要通过自监督的方式,实现股票信息的合理编码;实际应用时还需要有解码器将股票特征映射到广义嵌入空间;本文后续实验主要使用 LSTM 作为编码器来描述预测能力
2.3 实验分析
数据说明:
- 股票走势预测的基准评估使用 ACL18 (2014~2016 年的 88 只股票和对应 Twitter 文本)和 KDD17 (2007~2016 年的 50 只股票)两种数据集
- 宏观数据主要来自 FRED(美联储经济数据),包括国债利率、货币量 M1/M2、工业产值、失业率、基金利率、政府债务、通货膨胀率、消费者价格指数等宏观指标
评价指标:准确率和 MCC
不同模型对比:
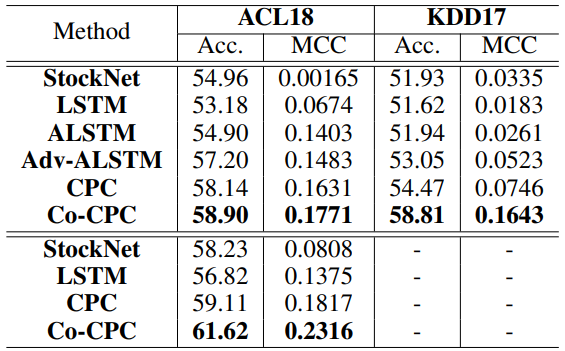
- ACL18 数据集上半部分只考虑价格信息,下半部分价格和推文信息都考虑
- Co-CPC 在所有情况下都取得了最好的结果(在 KDD17 中优势更明显)
考虑不同时间间隔的宏观指标(间隔越短,效果越好):
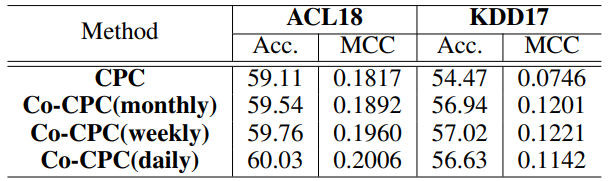
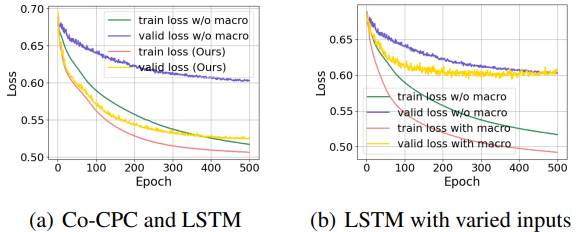
融入宏观指标能显著改善模型的泛化性能:
两种策略的投资回报模拟:
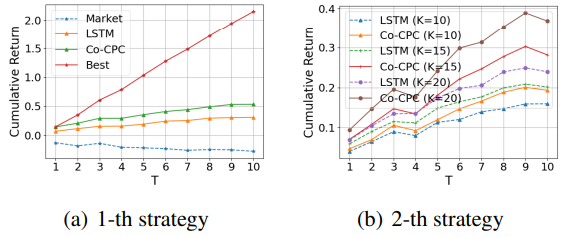
- 策略 1:持有所有预测次日收益为正的股票
- 策略 2:持有评分(上升概率-下降概率)最高且收益为正的前 K 个股票
- 选择的股票越多(K 越大),Co-CPC 获得的收益就比 LSTM 更多
其他分析结果:
- 影响最大的宏观因素 Top5:每日联邦基金利率(FFR)、每日10年期国债固定到期利率(DGS 10)、每日3个月期国债利率(TB 3)、每月工业产值(INDPRO)和每年消费者价格指数(CPI)