1 图嵌入表示
传统图机器学习 VS 图表示学习
- 给定输入图，传统图机器学习需要提取节点、链接和图级特征；然后学习将特征映射到/预测标签的模型（SVM、普通神经网络等），并应用于下游任务
- 图表示学习则不需要额外特征工程，而是给定输入图，自动学习独立于任务的特征（节点、链接和图级嵌入表示），然后用于算法的训练学习和下游任务
嵌入表示的好处：
- 节点间嵌入的相似性表明了它们在网络中的相似性
- 嵌入表示编码了很多网络信息，可用于很多下游任务
嵌入表示的可视化示例（数据源：Zachary 空手道俱乐部网络节点）
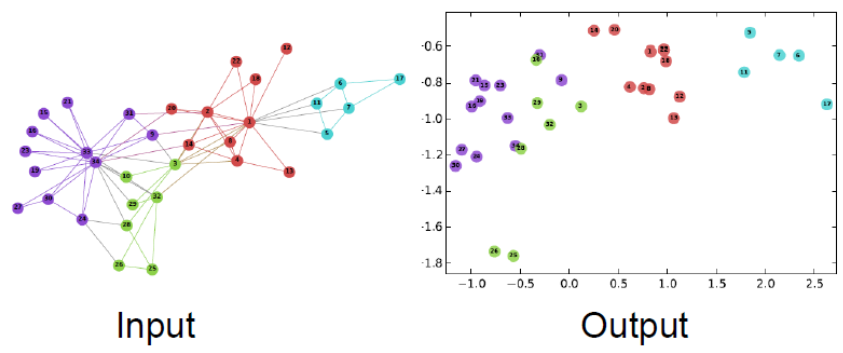
2 编码与解码
节点编码：将原始网络中的节点映射到嵌入空间，得到节点的低维嵌入表示
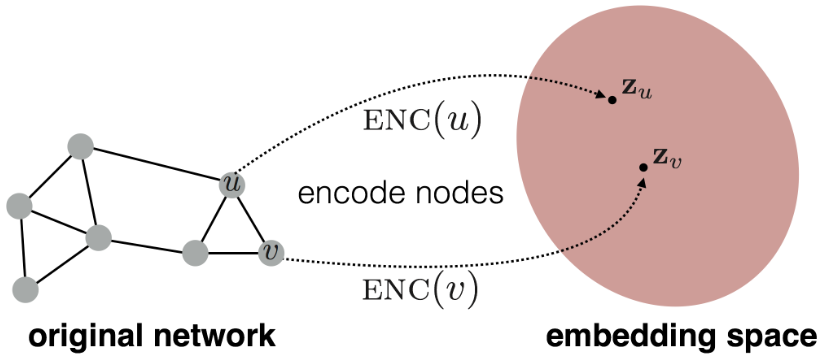
节点编码的原则：两个节点的相似度在原始网络和嵌入空间中保持一致，即 $$similarity(u,v)\approx z_v^Tz_u$$
- $similarity$ 为节点相似度函数，用于度量两节点在原始网络中的相似度
- 考虑使用两个节点嵌入表示的点积来度量两个节点在嵌入空间中的相似度
思考：如何度量两节点在原始网络中的相似度？
节点间存在链接？有相同的邻接节点？有相似的子图结构？
3 基于随机游走的节点嵌入
图上的随机游走示例：
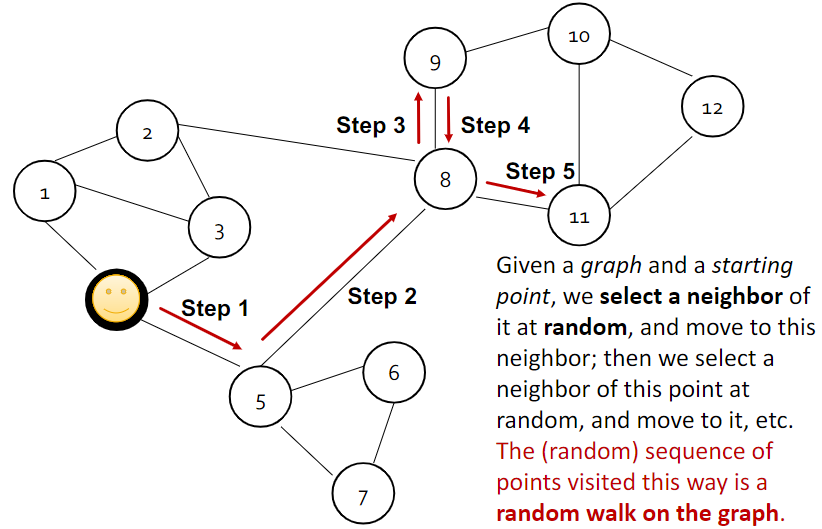
- 以"笑脸"节点为出发点，随机选择并移动到一个邻接节点
- 重复以上过程，实现在图上的随机游走（路线可重复）
给定随机游走策略 $R$ ，可定义节点相似度为：
$$P_R(v|u): 以节点u为起点，随机游走经过节点v的概率$$
而向量的点积对应向量夹角的余弦相似度 $cos(\theta)$。因此随机游走场景下，节点嵌入表示应该追求 $cos(\theta)$ 与游走共现概率 $P_R (v|u)$ 的一致性
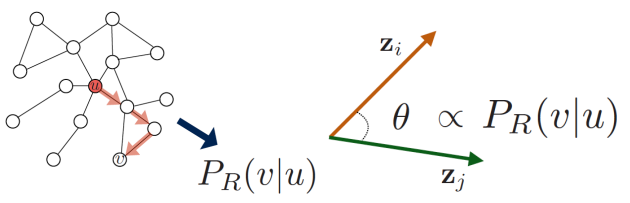
游走共现概率这一统计量，包含了节点的局部和高阶邻域信息
4 节点嵌入的目标函数
定义 $N_R(u)$ 为节点 $u$ 通过随机游走策略 $R$ 经过的节点集合
$N_R(u)$ 中可以有重复元素，因为节点可以在随机游走中被多次访问
随机游走策略 $R$ 的步长一般比较短（防止距离 $u$ 较远的节点纳入 $N_R(u)$）
目标函数可定义如下（softmax 形式）：
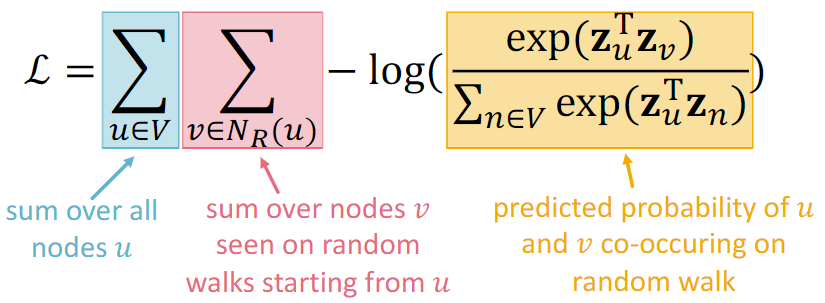
- 即寻找最优的嵌入表示 $z$, 以尽可能增大节点 $u$ 与其邻近节点 $v$ 相似度
问题：Softmax 形式的目标函数计算复杂度太高了（达到了 $O(|V|^2)$）
方案：考虑使用负采样（Negative Sampling）来实现快速似然计算
$$ -\log(\frac{\exp(\mathbf{z}_u^\mathrm{T}\mathbf{z}_v)}{\sum_{n\in V}\exp(\mathbf{z}_u^\mathrm{T}\mathbf{z}_n)}) \approx \log\left(\sigma(\mathbf{z}_u^\mathrm{T}\mathbf{z}_v)\right)+\sum_{i=1}^k\log\left(\sigma(-\mathbf{z}_u^\mathrm{T}\mathbf{z}_{n_i})\right),n_i{\sim}P_V $$
- 随机选择 $k$ 个负样本来实现 softmax 近似
- $k$越大，计算成本越高，估计结果越可靠（$k$ 一般取值为 5~20）
以上两小节的随机游走策略与目标函数构成了 DeepWalk 的基本思路
而 则改进了 DeepWalk 随机游走策略，实现更有效的网络信息保留
5 随机游走策略的改进
node2vec：有偏的、局部与全局视角权衡的随机游走
metapath2vec：基于节点属性的有偏随机游走
Learning Node Embeddings via Graph Attention：基于可学习参数的随机游走
LINE：基于 1 跳和 2 跳随机游走概率（一阶/二阶邻近度）进行优化
struc2vec：修改原始网络后再允许随机游走（基于结构评估相似性）
思考：如何取舍不同的算法和方案？
没有一种方法是适合所有情况的（比如 node2vec 可能更适合节点分类任务，但随机游走一般情况下都比较有效），需要根据具体的业务场景选择合适的节点相似度定义
6 整图的嵌入表示
整图嵌入表示的应用场景：识别分子毒性，识别异常的图结构
整图嵌入表示的 3 种方法：
- 先使用常用的节点嵌入方法，整图嵌入表示就是所有节点嵌入表示的加和/均值
- 引入"虚拟节点"来表示（子）图，之后再使用常用的节点嵌入方法来表示该节点
- 先对图中节点进行分层聚类，然后对每个集群计算对应节点嵌入表示的加和/均值
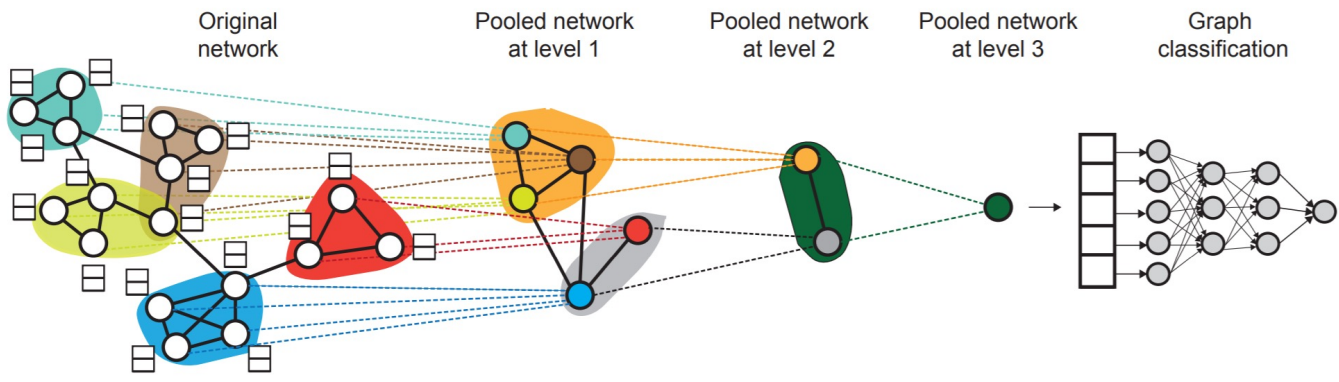
方法 1 可参阅论文《 Convolutional Networks on Graphs for Learning Molecular Fingerprints》 方法 2 可参阅论文《Gated Graph Sequence Neural Networks》 方法 3 可参阅论文《Hierarchical Graph Representation Learning with Differentiable Pooling》
7 矩阵分解与嵌入表示
假设节点相似性的定义如下：当节点 $u$ 与节点 $v$ 直接相连时，二者是相似的
则节点 $u$ 的嵌入表示 $z_u$ 和节点 $v$ 的嵌入表示 $z_v$ 满足： $$ z_v^Tz_u=A_{u,v} $$
- 其中 $A$ 表示邻接矩阵
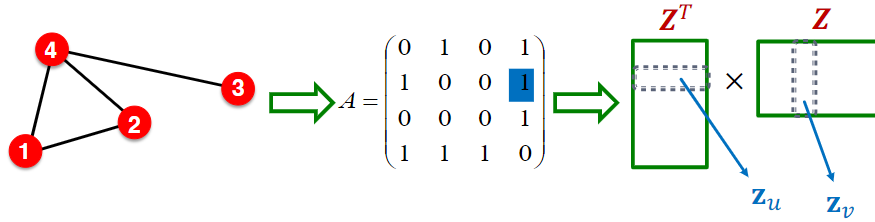由此可知，$Z^TZ=A$ ；其中嵌入维度 $d$（$Z$ 的行数）远小于节点数 $n$
精确的分解 $A=Z^TZ$ 一般是不可能的，但可以定义目标函数如下： $$ min_Z|||A-Z^TZ|^2 $$
- 虽然和节点嵌入表示算法的目标函数存在差异，但二者的目标是相同的
- 由此可知，根据边连通性定义的节点相似度而的得到的编码器（将原始网络中的节点映射到嵌入空间的低维表示），其作用相当于对邻接矩阵 $A$ 进行矩阵分解
DeepWalk 等基于随机游走的节点相似度定义的编码器，相当于复杂矩阵的分解
更多解释和细节可参阅论文：《Network Embedding as Matrix Factorization》
8 嵌入表示的应用与局限性
应用方向：
- 聚类/社区检测：根据节点的嵌入表示进行聚类
- 节点分类：根据节点的嵌入表示进行标签预测
- 边分类：通过节点嵌入来计算（连接/求和/乘积/求差）边的嵌入
- 图分类：通过节点嵌入来聚合或构建"虚拟节点"来表示图
节点嵌入表示的局限性：
- 直推式学习（transductive learning）：无法为训练中没有见到的节点生成嵌入表示
- 无法捕获结构相似度（下图中节点 1 和节点 11 在结构上相似，但嵌入表示截然不同）
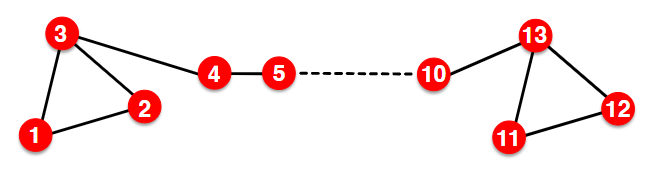
- 无法利用节点、边和图的特征（例如蛋白质的特性和相互作用）
以上限制的解决方案：深度表示学习和图神经网络（后续课程）