1 计算图与邻域信息
关键问题:GNN 节点嵌入能否区分不同节点的局部邻域结构?
GNN 通过邻域定义的计算图生成节点嵌入:
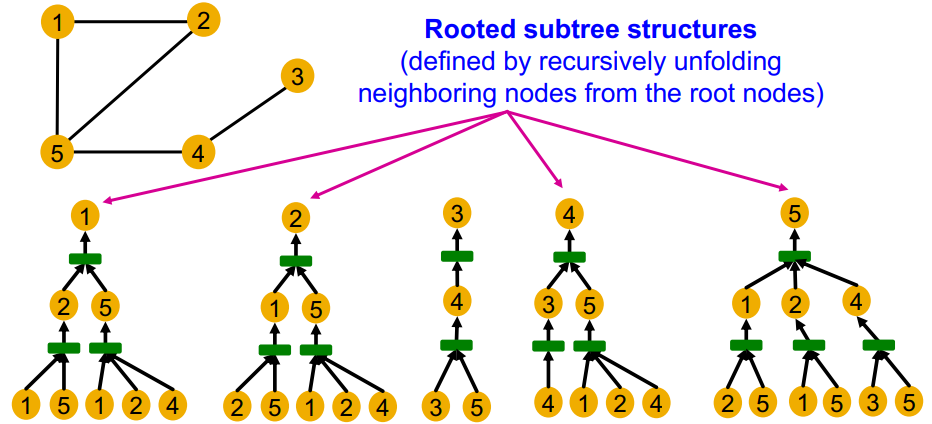
- 节点 1 和节点 5,因其度数不同而具有不同的邻域结构信息
- 节点 1 和节点 2,具有相同的邻域结构信息;二者在图中是对称的
- 节点 1 和节点 4,其 2 跳邻居的信息存在差异(邻居的度不同)
由于 GNN 主要依赖节点特征,而不考虑节点 ID
因此 GNN 无法区分位置同构的节点(节点 1 和节点 2)
2 GNN 的模型表达能力
单射(injective)函数:将不同的输入元素映射为不同的输出
直觉上考虑:单射函数 $f$ 保留了有关输入的所有信息
模型表达能力好的 GNN 模型应该能将不同的计算图单射到不同的节点嵌入:
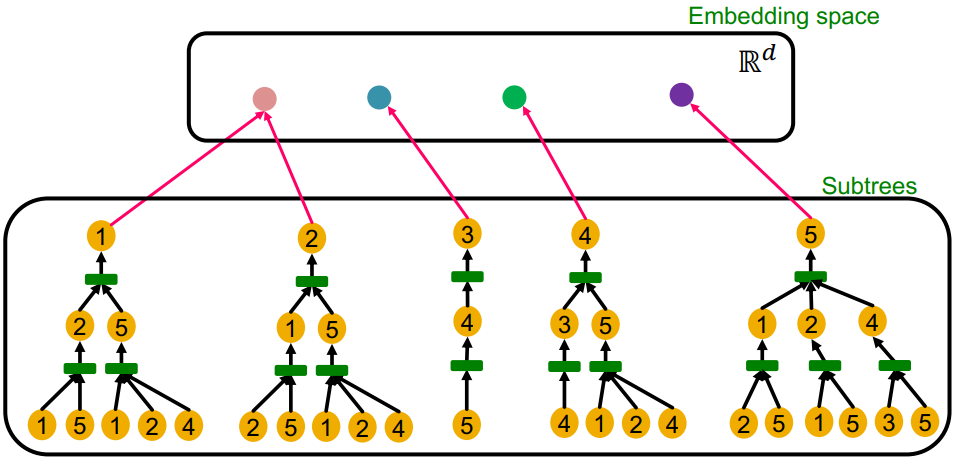
- 同深度的子树可以通过从叶节点迭代到根节点来实现信息的表征
启发:模型表达能力好的 GNN 模型应该在每一层中针对邻域信息使用单射聚合函数
这样 GNN 才能在聚合时尽量保留邻域信息,使得最终不同节点具备不同的嵌入表征
3 已有模型的表达能力局限
聚合函数能改善 GNN 的表达能力,尤其是单射聚合函数
概念补充:多重集(multi-sets),同一个元素可以出现多次的集合
邻域聚合函数的输入可定义一个由邻域节点组成的多重集
GCN 的邻域聚合分析:
- 邻域聚合过程:先逐元素取均值,在进行线性映射与 ReLU 激活
- GCN 的聚合函数无法区分具有相同颜色(相同特征值)比例的不同多重集
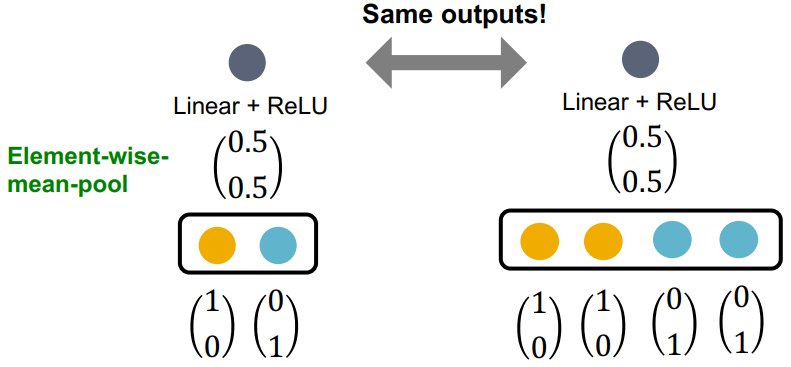
GraphSAGE 的邻域聚合分析:
- 邻域聚合过程:先应用 MLP ,再逐元素取最大值
- GraphSAGE 的聚合函数无法区分具有唯一颜色相同的不同多重集
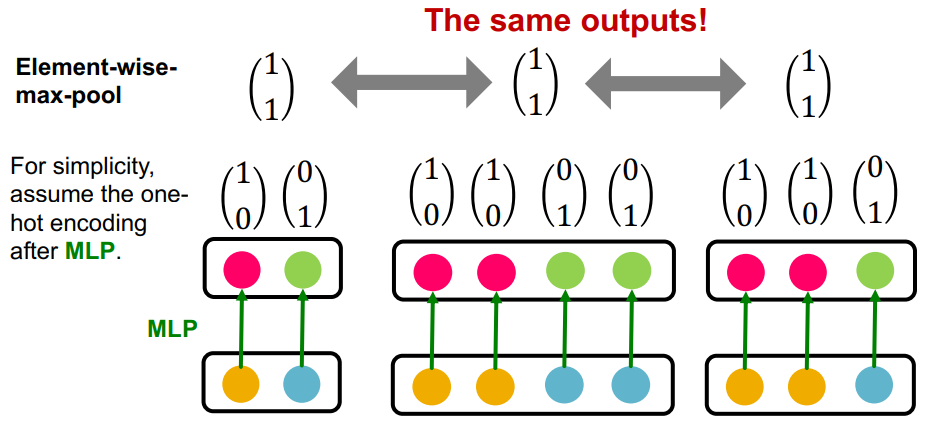
总结:由于邻域信息聚合函数都不是单射的, GCN 和 GraphSAGE 存在局限性
思考:如何设计出最具表达能力的模型?
回答:在多重集上构建一个单射的邻域聚合函数
4 图同构网络 GIN
前置知识:WL 图同构检验
在 WL 图同构检验算法中,使用单射 HASH 函数对邻域信息进行聚合: $$ c^{(k+1)}(v)=\mathrm{HASH}\left(c^{(k)}(v), \left\{c^{(k)}(u)\right}_{u\in N(v)}\right) $$
- 其中 $c^{(k)}(v)$ 表示根节点的特征,$\left{c^{(k)}(u)\right}_{u\in N(v)}$ 表示邻节点的特征
借助 MLP 的强大拟合能力,GIN 实现了逼近 WL 的邻域信息聚合能力: $$ \mathrm{GINConv}\left(c^{(k)}(v), \left\{c^{(k)}(u)\right}_{u\in N(v)}\right)=\mathrm{MLP}_\Phi\left((1+\epsilon)\cdot\mathrm{MLP}_f(c^{(k)}(v)))+\sum_{u\in N(v)}\mathrm{MLP}_f(c^{(k)}(u))\right) $$
- 上式右侧满足单射函数处理多重集 $S$ 时的通用格式, $\Phi(\Sigma_{x\in S}f(x))$
- 上式右侧中, $\epsilon$ 为可学习的标量参数,用于平衡节点本身的信息与邻域信息
- GINConv 作为可微函数,对 WL 图同构检验算法中的 HASH 函数进行替代
GINConv 函数的目的是确保将不同的输入映射到不同的嵌入
GIN vs WL 算法:
- WL 算法使用 HASH 函数更新,更新目标是节点的颜色(one-hot 格式)
- GIN 的更新函数 GINConv 是可微的,可以结合下游任务进行参数的更新
- GIN 更新的节点嵌入是低维向量,可以捕捉到不同节点的细粒度相似性
- GIN 借助 MLP 实现逼近 WL 算法的性能,二者均具备较强的图区分能力
不同池化层的表达能力排序:sum > mean > max
5 补充:图训练技巧
针对第二次课下作业的一些图训练的技巧补充
数据预处理:对节点属性进行标准化处理
优化器:Adam 对学习率相对稳健
激活函数
- ReLU 函数一般效果较好
- 其他替代方案:LeakyReLU、PReLU
- 输出层不需要激活函数;每层都会有偏置项
嵌入表示尺寸:32、64 和 128 通常是很好的起点
训练不收敛问题:依次排除 Pipeline、学习率等超参、参数初始化、损失函数
模型开发注意事项:小样本数据任意过拟合;监控训练和验证的损失曲线