中文标题:在没有人工演示的情况下求解奥林匹克几何
英文标题:Solving olympiad geometry without human demonstrations
发布平台:Nature
发布日期:2024-01-01
引用量(非实时):145
DOI:10.1038/s41586-023-06747-5
作者:Trieu H. Trinh, Yuhuai Wu, Quoc V. Le, He He, Thang Luong
关键字: #几何 #AlphaGeometry #IMO
文章类型:journalArticle
品读时间:2024-08-08 15:46
1 文章萃取
1.1 核心观点
- 本文的 AlphaGeometry 在已有推理演绎引擎的基础进行大胆创新,先融合了自动化几何演绎数据库(DD)和代数规则(AR),然后借助生成式 LLMs 模型推算相关几何问题的辅助结构;最终的 AlphaGeometry 在 IMO 真题和其他奥数题测试表现出色,接近 IMO 金牌得主的平均水平;并且 AlphaGeometry 的输出结果是人类可读的,也还具备深入挖掘的潜力
1.2 综合评价
- 首个在平面几何定理证明方面超过普通 IMO 参赛者的计算机程序
- 继承和改进已有符号演绎引擎,还结合生成式 LLMs 进行辅助增强
- 论文结构清晰,读起来很舒服;整体的思路可以拓展到其他领域
1.3 主观评分:⭐⭐⭐⭐⭐
2 精读笔记
2.1 背景知识
几何问题的特点:
- 几何问题的语言定义狭窄,不能表示复数、辅助结构等的额外信息或工具
- 目前的解决方法主要依赖符号方法和人类设计的硬编码搜索启发式算法
交互式定理证明器和编程语言 Lean:
- 由微软研究院开发,结合了编程语言和逻辑推理的功能
- 使用户能够定义数学对象、编写证明和验证算法的正确性
- 而
nlinarith和ring则是两种集成在Lean内的符号引擎
nlinarith:用于非线性算术推理,可处理多项式不等式和等式
在 Lean 中使用 nlinarith 的示例:自动证明 $a \times b + 1 \geq 1$,前提是 $a \times b \geq 0$:
example (a b : ℝ) (h : a * b ≥ 0) : a * b + 1 ≥ 1 :=
begin
nlinarith,
end
ring:用于处理环结构中的符号计算,可自动化证明和简化多项式等式
在 Lean 中使用 ring 的示例:自动证明 $(a + b)^2 = a^2 + 2ab + b^2$
example (a b : ℕ) : (a + b) * (a + b) = a * a + 2 * a * b + b * b :=
begin
ring,
end
2.2 算法细节
AlphaGeometry 专注于解决平面几何问题,因此排除了几何不等式和组合几何等主题
2.2.1 定理和证明的数据合成
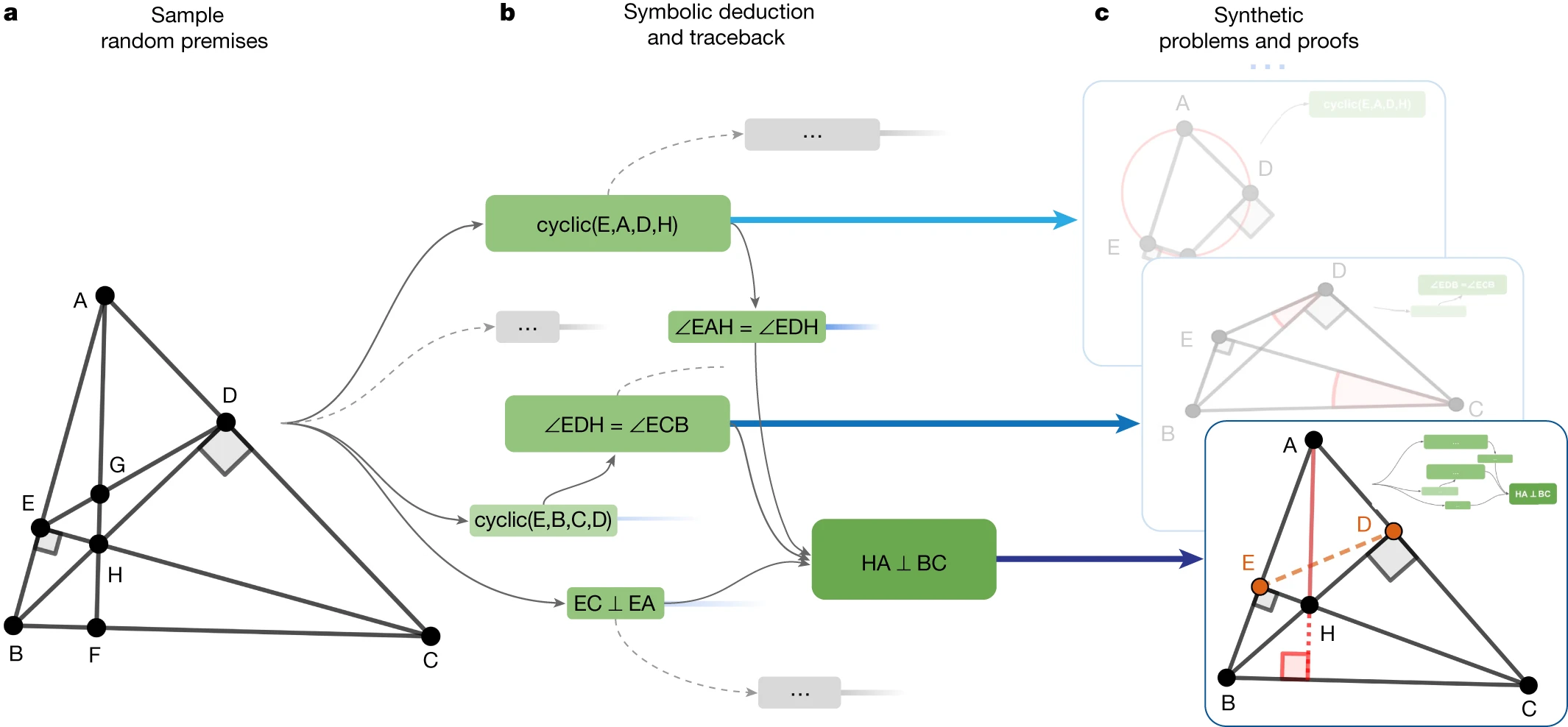
- 步骤 a:先在一组大型随机定理数据中进行均匀采样,作为符号演绎引擎的前提输入
- 步骤 b:基于前提输入,使用符号演绎引擎进行前向推理,得到新的真值陈述,并作为节点构成有向无环图;这样对于图中的每个节点,都可以通过回溯找到该推导语句的最小必要前提和依赖项(例如节点
HA⊥BC可以通过回溯得到图中的绿色子图) - 步骤 c:包含最小必要前提的依赖子图构成了一个平面几何问题及其解过程(存在辅助线);最终的训练样本由前提 $P$、结论 $N$ 和证明 $G(N)$ 组成
前提 $P$ 是最小必要前提的集合,对于结论节点 $N$ 进行回溯可以得到其依赖子图 $G(N)$
细节补充:符号演绎引擎
- 在符号引擎的基础上进行演绎推理,具体实现是 DD 和 AR 两种组件的复杂集成
- DD(Deductive Database)是一种自动化几何演绎数据库,结合了传统数据库和逻辑编程的推理能力;允许用户通过逻辑规则和事实来查询和推理数据;给定一组几何规则或公理,程序可以找到其不动点(fixpoint),能反映了该几何系统的所有关键属性(参考论文)
- AR(Algebraic Rules)则可以通过代数规则进行新语句的推导(简单来说,就是借助高斯消元过程将每个变量表示为剩余变量的唯一线性组合),该方法对于角度、比例和距离的计算是必要的,也是对几何证明过程的一种补足(进阶阅读的可参考资料 )
- DD 和 AR 通过交替执行来实现推理能力的增强:DD 输出通过演绎规则,推导出新的陈述语句并输入 AR;AR 执行后也会产生新的等式,作为 DD 下一次迭代的输入;如此循环,直到联合推理闭包停止扩展(也就是不能再推导出新的结论了)
符号演绎引擎的示例(DD+AR):

DD 和 AR 的组合,是本文工作的一个创新点,代表了几何符号推理的新技术水平
实际应用时,本文对 DD 组件进行改进,使用图结构来更全面地表示几何关系,这种存储结构不仅能捕获几何形状的对称性,也包含了几何性质(相等性、共线性和环性等)的传递性;这些隐式的推理规则,能提高了几何推理的效率和表达能力
对于几何规则的回溯,其本质是一种最小生成树的搜索过程(1_study/math/NP-Hard 问题),本文主要使用贪婪算法来实现;对于代数规则的回溯,其等效于混合整数线性规划问题(找到满足计算的最小前提集);对于辅助结构,则通过随机弃置、详尽试错的方式来找到最小前提子集
2.2.2 生成超越符号推理的证明
对于奥林匹克级别的几何问题,目前的符号演绎引擎仍存在不足,原因如下:
- 抽象说法 1:存在缺失项,构成了结论 $N$ 独立于前提 $P$ 的子集
- 抽象说法 2:结论陈述和结论对象之间存在依赖关系差异
- 非抽象说法 1:演绎引擎的推理能力有限,需要额外的信息补充
- 非抽象说法 2:为演绎引擎提供辅助结构信息,能有效改善其性能
辅助结构是所有证明搜索算法绕不开的难题;辅助结构的引入可能导致推理树产生无限的分支(算力是有限的);目前辅助结构的引入方法主要依赖手工制作的模板和特定的启发式方法
本文的另一个亮点,就是引入生成式 LLMs 来实现辅助结构的自动构建
生成式 LLMs 的训练/微调过程(更多模型结构的细节可参考该论文):
- 训练阶段:将上一节生成的 1 亿个训练样本按照
<前提><结论><证明>的形式进行序列化处理,转化为符号组成的文本字符串,然后通过基于 GPT 结构的深度神经网络进行训练;最终模型能根据<前提><结论>的输入,实现<证明>的生成 - 微调阶段:筛选训练样本中需要辅助结构的 900w 个证明(占比 9%), 然后用于模型微调;最终的模型能根据
<前提><结论>的输入,给出更合理的辅助结构建议,比如"构造点 X,使 ABCX 是平行四边形"
实际推理时,符号引擎会考虑探索 LLMs 给出的前 k 个辅助结构(波束搜索)
最终 AlphaGeometry 的推理过程:
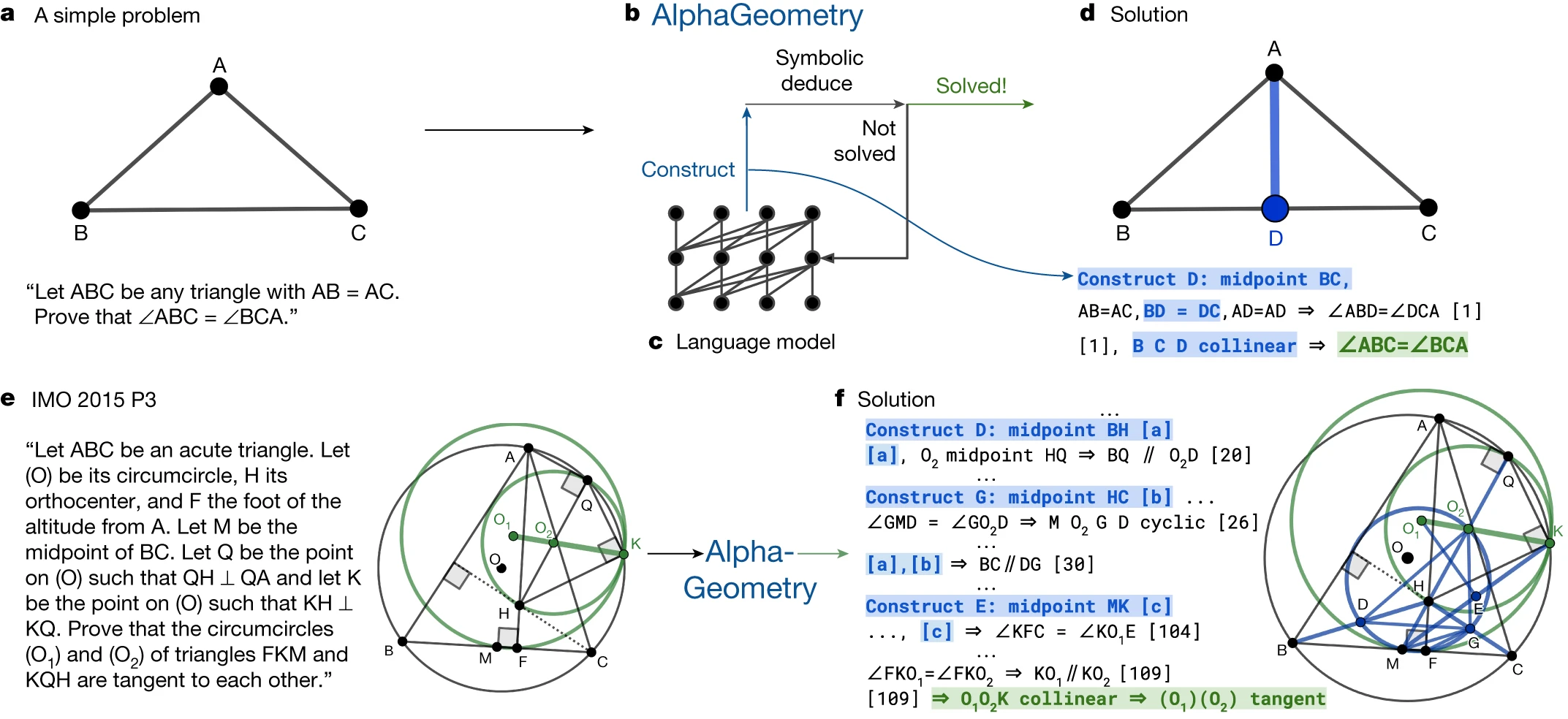
- (1)给定一个需要证明的定理,将
<前提><结论>输入模型(2)AlphaGeometry 通过循环调用符号推导引擎和 LLMs 来实现整个推理过程;当符号引擎无法实现证明时,LLMs 会构建一个辅助点,并输入到符号引擎再次进行推理(3)当符号引擎实现证明,或循环次数达到最大时,推理结束 - 图 a,图 b 和图 c 通过一个简单的定理证明,描述了这一推理过程
- 图 e 和图 f 则来自 IMO2015 年的真题 3,AlphaGeometry 为解决该问题构建了 3 处辅助点
从图可知,AlphaGeometry 的结果是人类可读的,不同于过往的计算机程序证明结果
2.3 结果评价
AlphaGeometry 的平面几何推理水平,接近 IMO 的金牌得主:
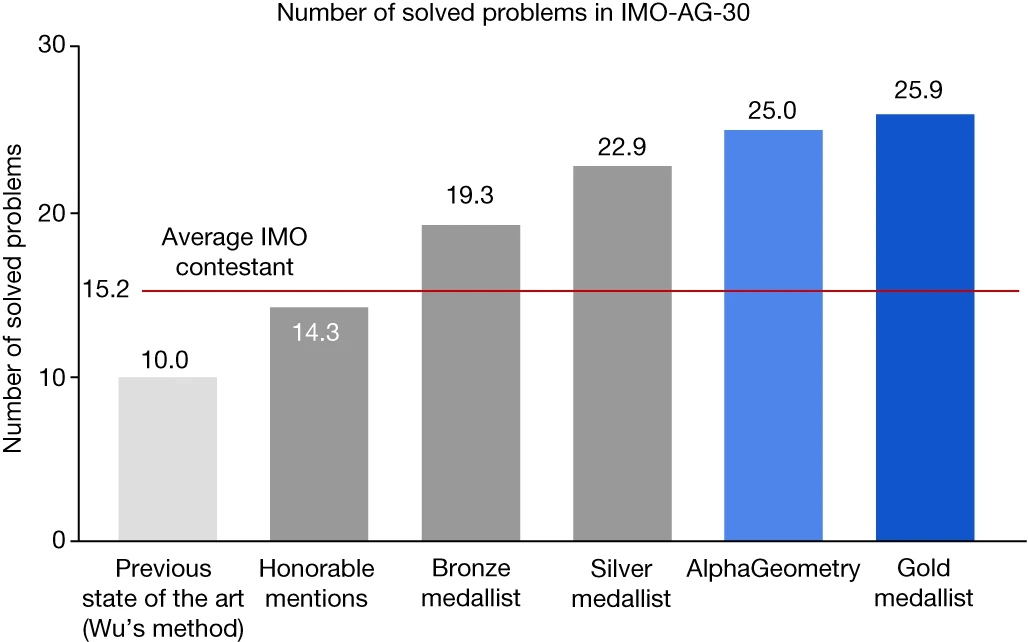
- 测试集涵盖了 2000~2013 年期间的 30 道 IMO 经典几何问题(排除组合几何)
- 此前的最优算法为计算机代数方法(Wu's method),该方法先将几何语句转化为点坐标形式的多项式方程,然后通过专门的大型多项式变换来完成证明(结果不具备人类可读性,且计算成本高)
- 在所有方法中,AlphaGeometry 取得了最好的成绩(解决了 25 道问题)
消融实验分析显示:
- 仅使用自动化几何演绎(DD)能解决 7 个问题;而 DD+AR (代数规则)能解决 14 个问题;最好的基线(DD + AR + 人为设计的启发式方法)解决了 18 个问题
- 当 LLMs 没有经过预训练时,AlphaGeometry 只能解决 21 个问题;当 LLMs 没有经过微调时,AlphaGeometry 只能解决 23 个问题(预训练和微调都很有效,前者更重要)
- 只使用 20%的训练数据,AlphaGeometry 依然能解决 21 个问题;波束搜索的 k 值减少 64 倍或深度减少 8 倍,也会得到类似的结果(解决 21 个问题)
通过搜集其他教科书练习题、区域性奥数题和著名定理,本文构建了 231 个几何问题集合进行了更丰富的测试:Wu‘s method 的准确率为 75%,DD + AR + 人为设计的启发式方法的准确率为 92.2%,本文提出的 AlphaGeometry 的准确率为 98.7%(与 IMO 测试结果一致)
合成证明数据的分析:
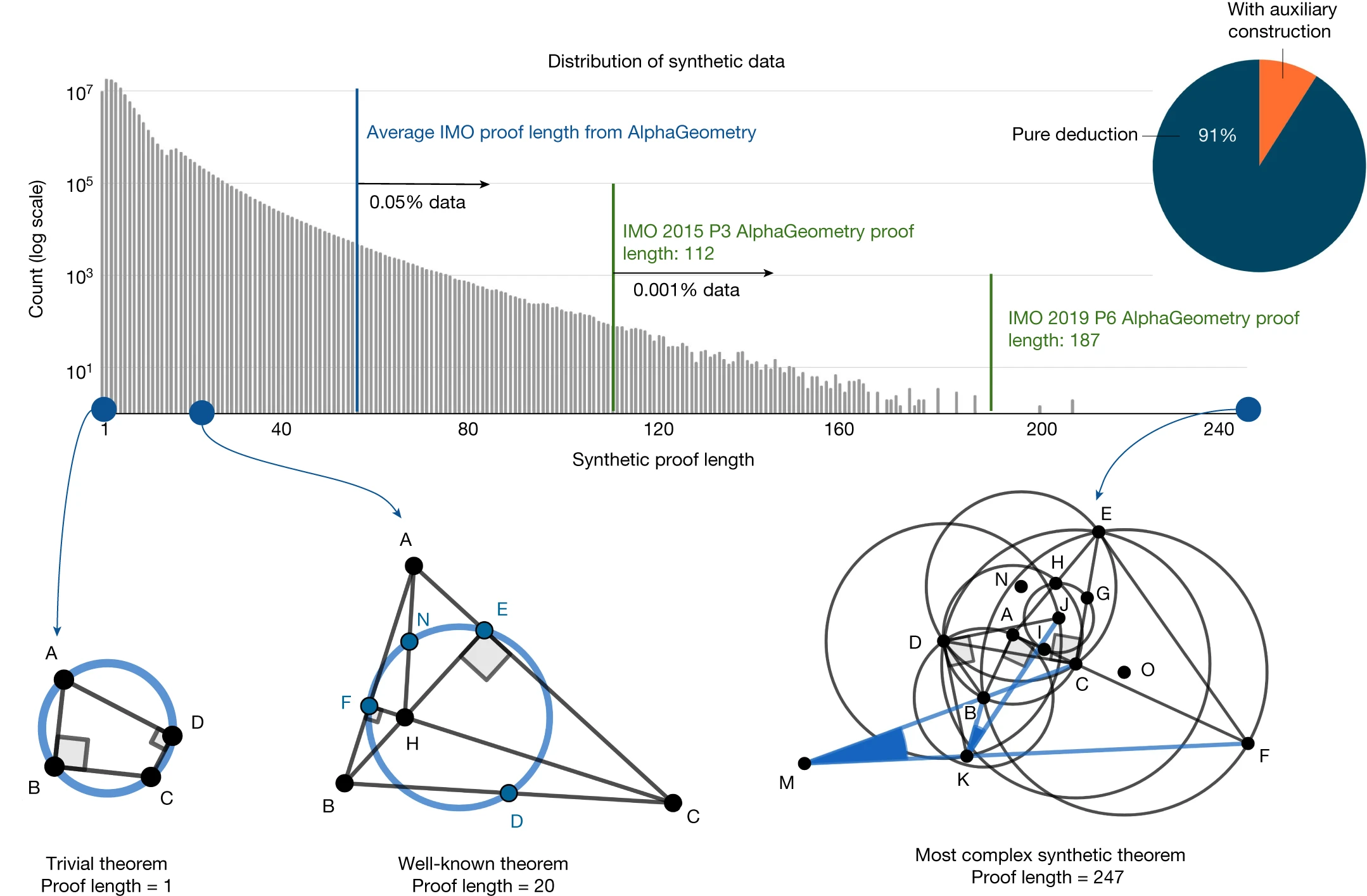
- 删除重复数据后,最终保留了超过 1亿条唯一定理和证明(注意 y 轴是对数化的)
- 合成数据中重新发现了很多已知的复杂定理和引理,有的甚至具备更强的通用性
- IMO 的 30 道几何真题不在合成数据的范围内,说明几何定理的空间仍然很大
- 在生成的合成证明中,有 9% 带辅助结构,有 0.05%超过了 IMO 真题的平均长度
- 最复杂的一个证明长度为 247,带两个辅助结构(合成的定理不偏向任何审美标准)
限制最大推理耗时与并行计算表现:
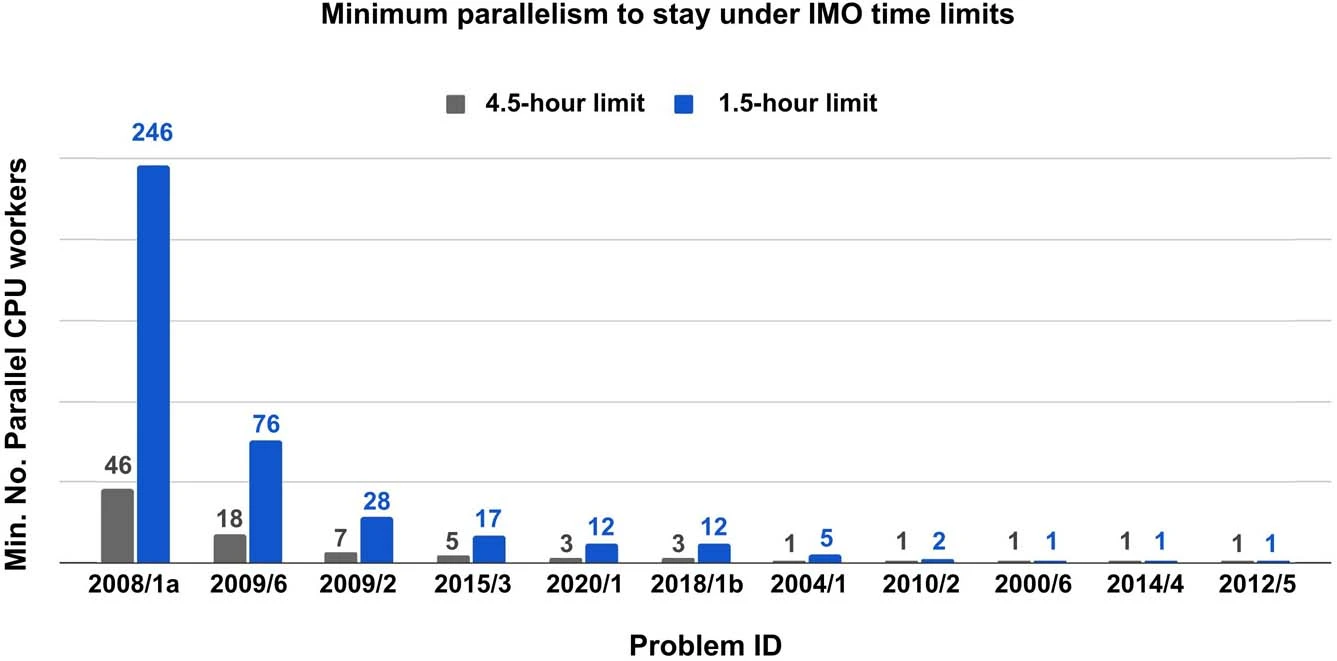
其他结论:
- 对于简单问题(人类平均得分>3.5),人类平均得分和证明的长度没有相关性(p=-0.06);而对于复杂问题,二者则存在较强的相关性(越难的题目对应的证明越长,也越需要辅助结构)
- 证明数据的合成,经过 10w 个 CPU 并行运行了 72h,生成了约 5 亿个样本;重新格式化规范形式后进行去重,并剔除包含在测试集内的样本,最终保留了 1 亿条合成数据
个人觉得对于几何问题的求解还是有一些取巧的成分(相当于 AI 借助了高级计算器)
3 后续发展
2024-07-11 NuminaMath 荣膺首届 AI 数学奥林匹克(AIMO)进步奖
2024-07-25 DeepMind 推出的两个数学推理模型在 IMO 比赛中大放异彩
- AlphaProof 通过确定答案并证明其是正确的,解决了两个代数问题和一个数论问题。这包括比赛中最难的问题,在今年的 IMO 上只有五名参赛者解决了这个问题
- AlphaGeometry 2 则证明了几何问题,只有剩余两个组合问题仍未解决
- 两个模型共获得了 28 分(满分 42 分),达到了与比赛中银牌得主相同的水平
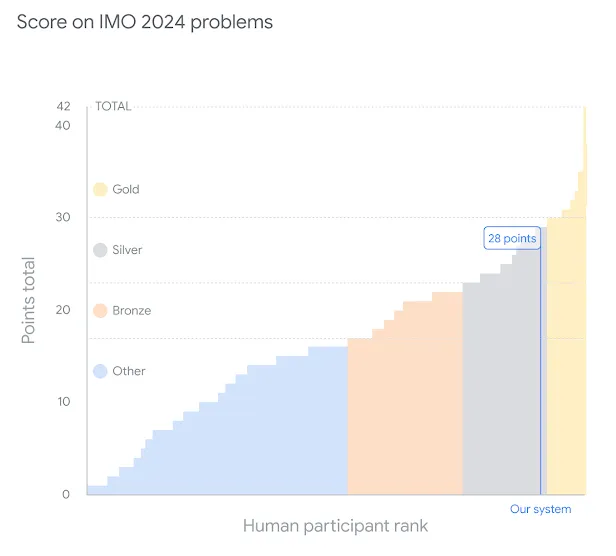
3.1 AlphaProof
一种基于强化学习的新型形式数学推理系统
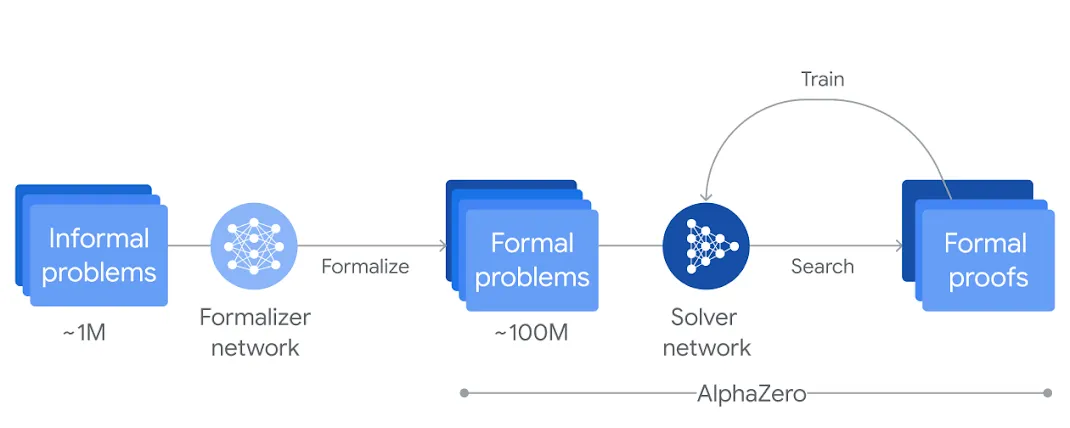
- 通过 1M 的数学问题微调 Gemini 模型后,将约 100M 个自然语言的数学问题陈述转化为 Lean 形式的正式数学语言;然后通过 LLMs 创建了一个跨难度的大型问题库(缓解数据不足的问题)
- 当遇到问题时,AlphaProof 的求解网络会生成候选解决方案,然后通过在 Lean 中搜索可能的证明步骤来证明或推翻方案;每个被验证的合理证明,都会通过 AlphaGoZero 的强化学习方法逐步训练并强化 AlphaProof 的求解网络,从而生成更优质的解决方案
3.2 AlphaGeometry 2
AlphaGeometry 2 是本文的改进版本
- 生成式 LLMs 改为基于 Gemini 的预训练(约 10 亿的训练样本)
- 更新符号引擎(快 2 个数量级),同时针对新问题使用了一种新颖的知识共享机制(具体没有细说 = =)来实现不同搜索树的高级组合,以解决更复杂的问题
- AlphaGeometry 2 可以解决过去 25 年中所有历史 IMO 几何问题的 83%;并且在 19 秒内就解决了 2024 年 IMO 赛题的几何问题(问题 4 的推理过程)
3.3 NuminaMath
7B 数学推理模型 NuminaMath
- 在数学解题的不同部分中尝试用 AI 协助或自动化
- 通过 LLM 生成 Python 代码,对数字答案进行暴力破解
- 预期用途是解决竞赛级数学问题,在几何问题上表现较差
- 该模型在 AI 数学奥林匹克(AIMO)中取得第一名(29/50)
目前已开源:模型下载地址