1 量化的基本概念
量化 Quantization：
- 将模型参数的精度从较高位宽（如 FP32 ）映射到较低位宽（如 INT8）
- 量化目标是减少原始参数表示所需的位数，并尽可能保留原始参数的精度
- 量化能降低部署成本，加速推理；也会导致参数的信息丢失，影响模型性能
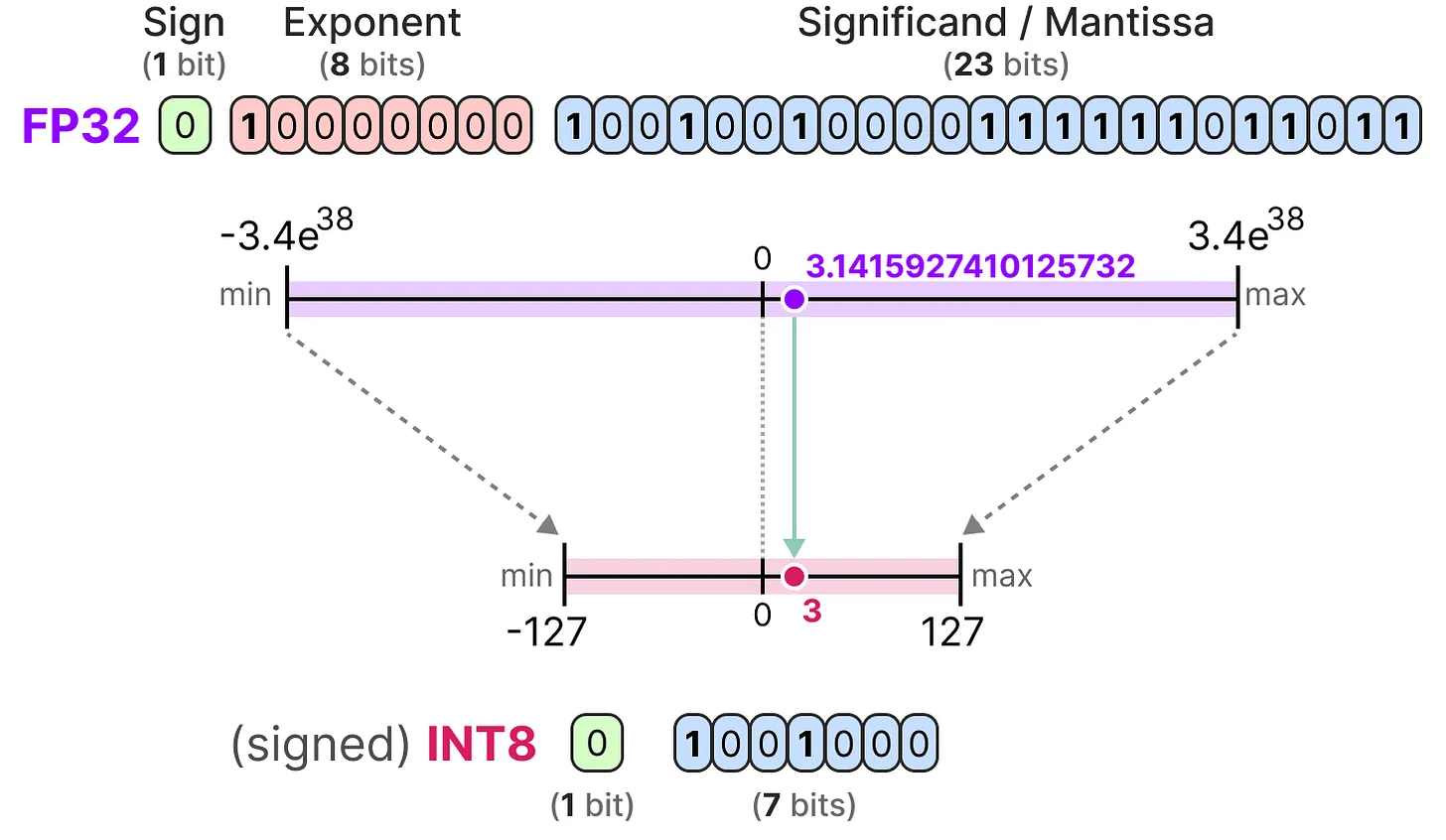
量化误差：将量化值还原后，得到的反量化值与原始值间的差异
量化中的异常值裁剪
- 给定向量中，可能存在一个值比其他值大很多的情况（即异常值）
- 此时可考虑手动设定量化后的范围，将超出范围的值映射为边界值
- 该方式会显著降低非异常值的量化误差，但也会增加异常值的量化误差
不同类型参数的量化
- 模型的权重和偏差值一般可视为静态值，其在运行模型之前是已知的；并且由于偏差值（数百万）比权重参数（数十亿）少很多，因此偏差值通常可以保持较高的精度（比如 INT16），而量化的重点也一般放在权重参数上
- 权重参数的常见量化范围校准（calibration）技术：（1）手动选择输入范围的百分位数（2）最小化原始权重和量化权重间的均方误差（3）最小化原始权重和量化权重间的 KL 散度
- 除此之外，还有激活值 activations 的量化，由于激活值会在推理过程中随着输入数据动态变化，因此激活值的量化难度较大，需要更进阶的量化方法（比如 PTQ 和 QAT）
- 对于长文本的推理生成，KV Cache 量化也是很有必要的；KV Cache 的本质上是空间换时间，通过缓存机制避免冗余计算；因此支持长文本的 LLMs，对应 KV Cache 的显存占用也较高，需要进行额外的量化处理
- 梯度值的量化相对小众，其在模型训练中时通常是浮点数；梯度值的量化能减少分布式训练中的通信成本，而能减少反向传播过程的计算开销
更低位数的量化（4 位，甚至 2 位）
- 量化误差会随着位数的减少而显著增加，因此一般不建议低于 4 位的量化
- 但目前也有一些技巧能实现 4 位（GPTQ 和GGUF）甚至 2 位的量化
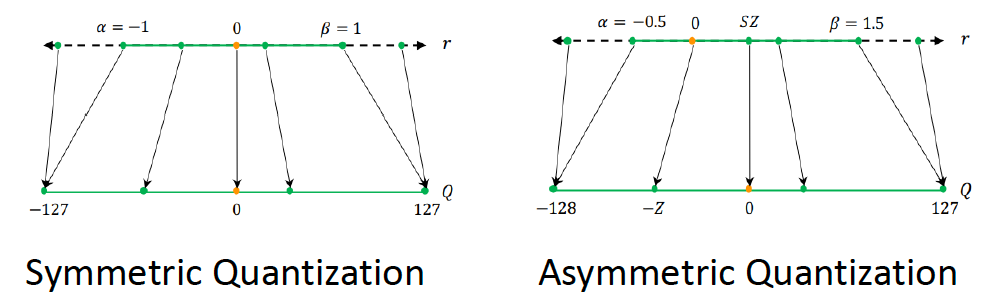
2 量化的对称性
Symmetric Quantization 对称量化
- 量化前后的范围保持以零为中心，即浮点空间中零的量化值恰好为零
- 最大绝对值量化（absmax quantization）是一种常见的对称量化形式
Asymmetric Quantization 非对称量化
- 与对称量化不同，浮点空间中零的量化值不再为零
- 零点量化（zero-point quantization）是一种常见的非对称量化形式
2.1 最大绝对值量化
absmax 量化使用最大绝对值 $\alpha$ 作为线性映射的范围
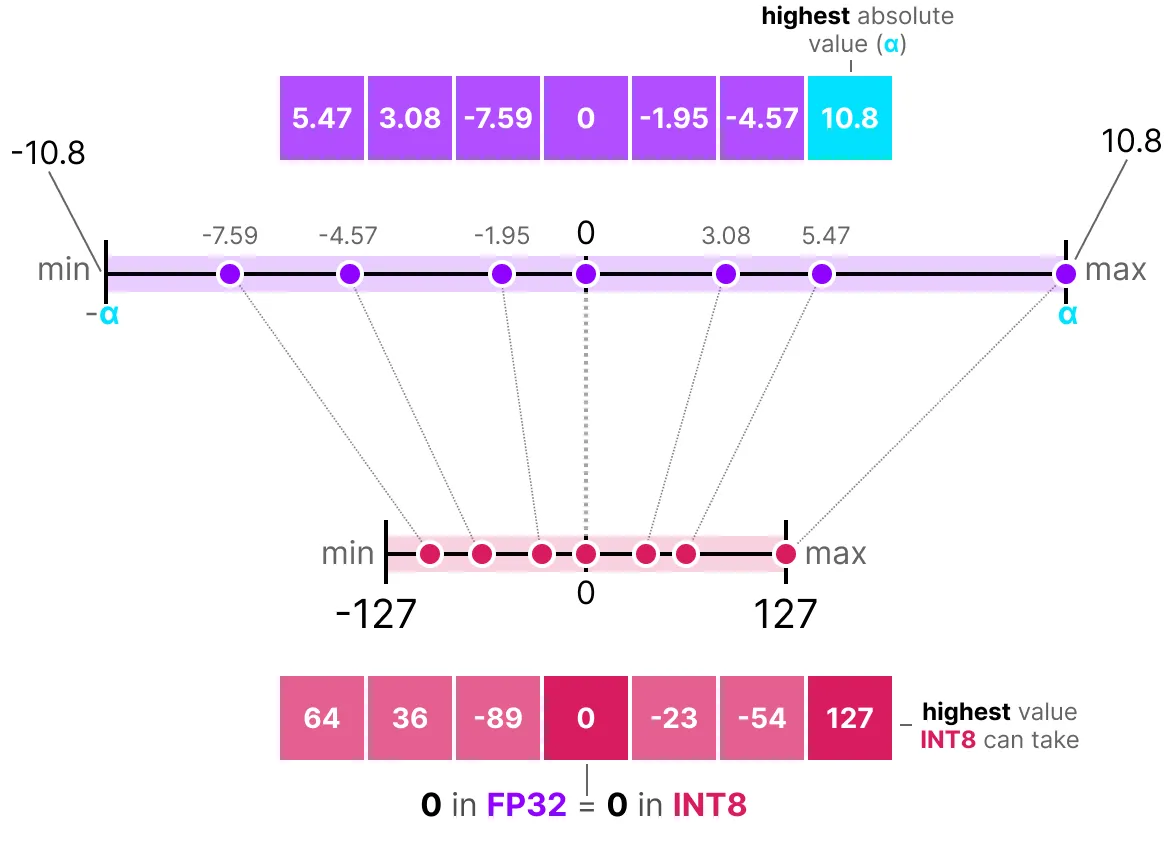
- 首先根据参数的最大绝对值 $\alpha$ 来确定缩放因子 $s$ ：
$$s=\frac{2^{b-1}-1}{\alpha}$$
- 然后对输入参数 $X$ 进行量化，得到 $X_{quantized}=round(s\cdot X)$
2.2 零点量化
零点量化使用浮点范围的最小值 $\beta$ 和最大值 $\alpha$ 作为线性映射的范围
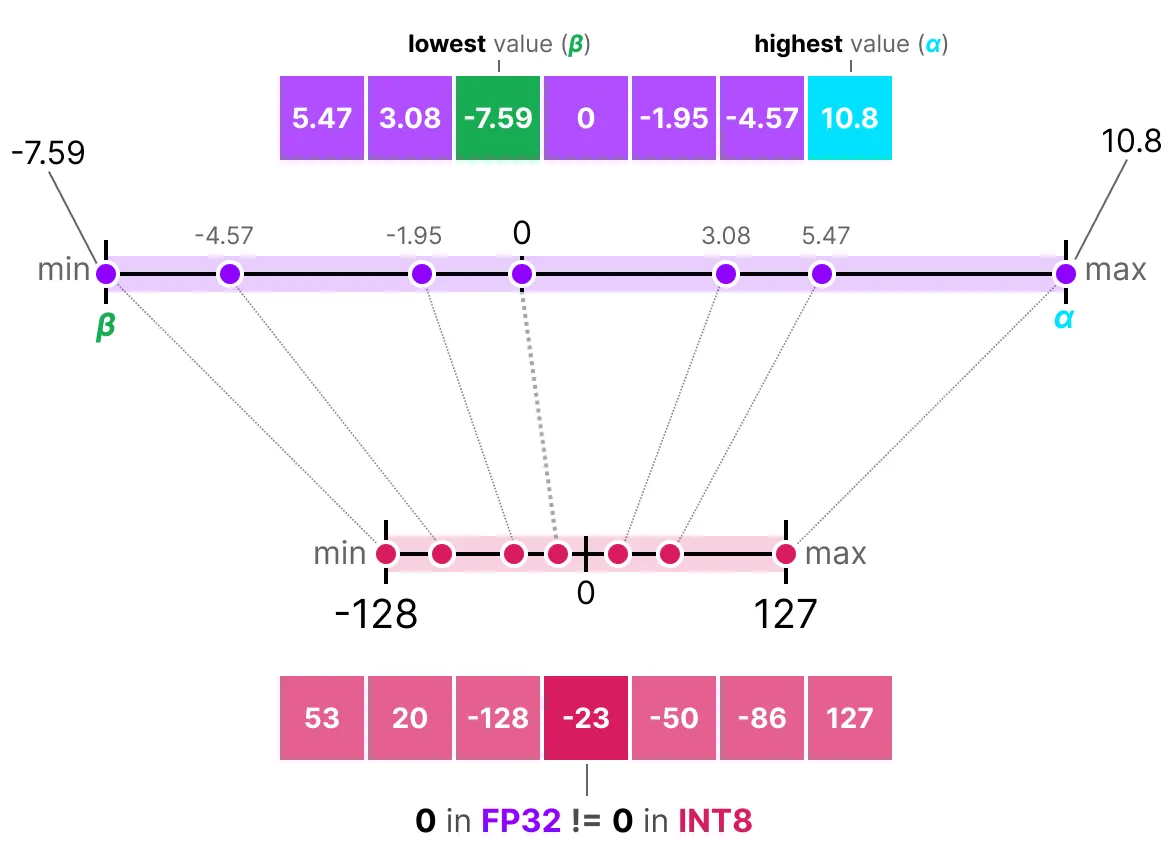
- 首先根据量化后的数值范围和原始参数的最小值 $\beta$ 和最大值 $\alpha$ 来确定缩放因子 $s$ ：
$$ s=\frac{127--128}{\alpha-\beta} $$
- 然后确定原始参数零点对应的量化值 $z=round(-s\cdot \beta)-2^{8-1}$
- 最后对输入参数 $X$ 进行量化，得到 $X_{quantized}=round(s\cdot X+z)$
3 不同阶段的量化
3.1 训练后量化 PTQ
训练后量化（Post-Training Quantization，PTQ）是一种流行的量化技术
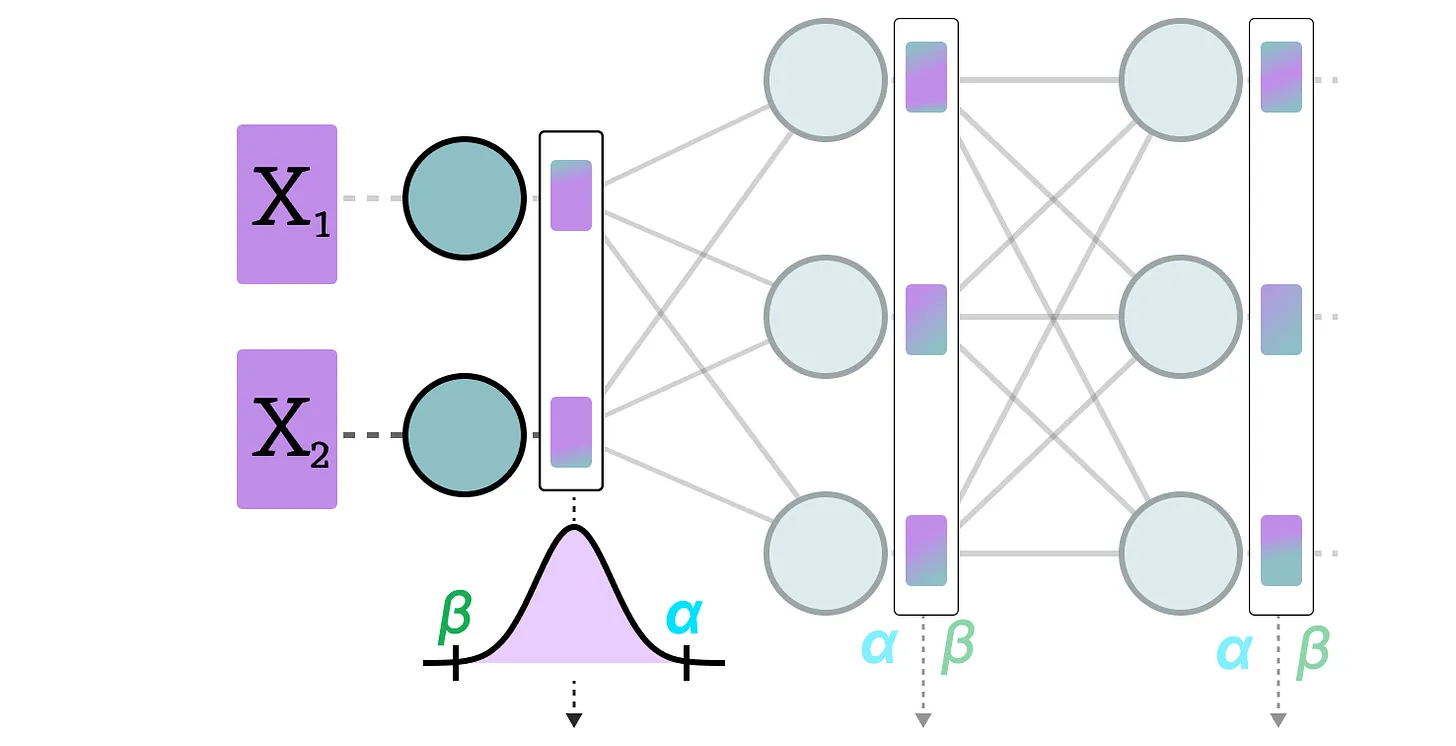
- 当输入数据经过隐藏层后收集其激活值，以此构建激活值的分布
- 根据激活值的分布找到原始参数的最小值 $\beta$ 和最大值 $\alpha$
- 使用和零点量化同样的方式，找到缩放因子 $s$ 和零点量化值 $z$
- 最后对输入参数 $X$ 进行量化，得到 $X_{quantized}=round(s\cdot X+z)$
注意：对于神经网络的每一层，PTQ 都要计算单独的缩放因子 $s$ 和零点量化值 $z$
动态量化 Dynamic Quantization VS 静态量化 Static Quantization
- 动态量化在推理过程中，计算缩放因子 $s$ 和零点量化值 $z$
- 静态量化使用校准数据集，提前计算并构建激活值的潜在分布
A8W8：对输入激活值进行 INT8 量化，对模型权重进行 INT8 量化
3.2 量化感知训练 QAT
量化感知训练（Quantization Aware Training，QAT）：
- 在模型训练期间学习量化过程，而不是仅针对训练后的模型进行量化
- 由于模型在训练阶段已经考虑到了量化，因此 QAT 往往比 PTQ 效果更好
- 但由于 QAT 的成本较高，因此 PTQ 通常更受欢迎，使用更广泛
QAT 的工作原理：
- 在训练过程中，先对参数值进行量化（quantize），再进行反量化（dequantize）
- 以此构建虚假的量化参数值（"fake" quants），使得模型考虑参数量化情况下的损失计算和权重更新，由此引导模型在训练过程中，追求更小的量化误差
QAT 的效果分析：
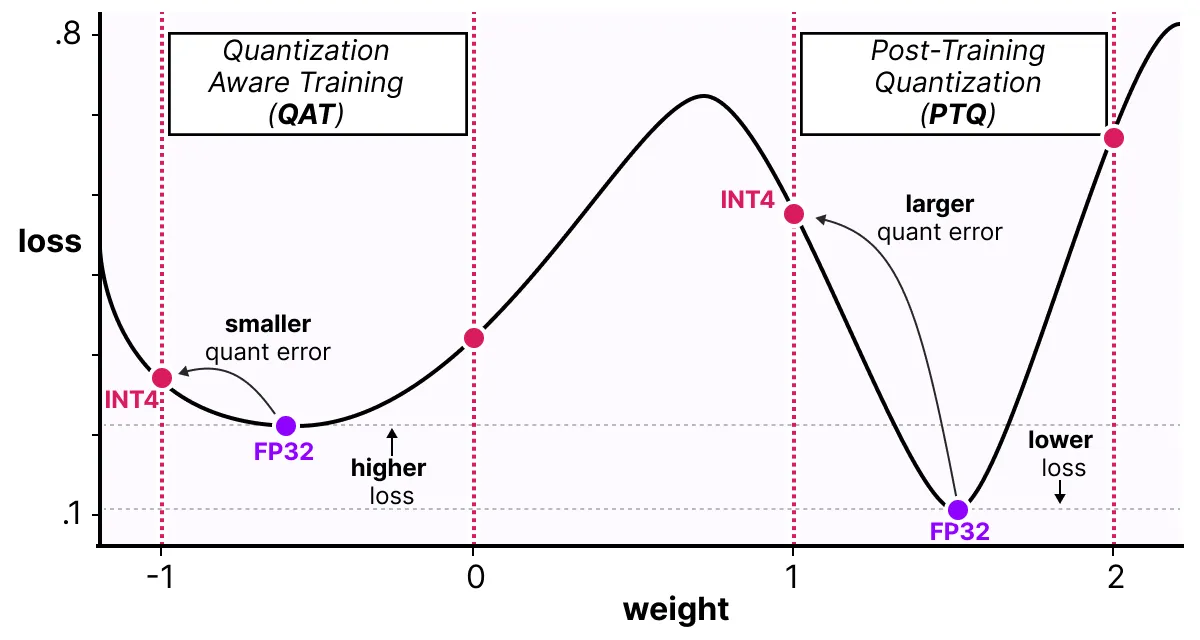
- 由于在模型训练阶段引入了 QAT，因此即使最终的模型损失可能会相对偏高
- 但相对于 PTQ，基于 QAT 模型参数的量化误差（quant error）往往会更小
3.3 量化感知微调 QAF
量化感知微调（Quantization-Aware Fine-tuning，QAF）
- 通过将量化感知整合到微调中，实现模型压缩和保持性能之间的平衡
- 具体的实现思路和 QAT 差不多，只不过阶段不同（预训练阶段 vs 微调阶段）
- QAF 的概念相对较新，本节以 PEQA 为例进行说明（QLoRA 也是一种 QAF）
参数高效微调（PEFT）仅微调少量 (额外) 模型参数，同时冻结预训练 LLM 的大部分参数，从而大大降低了计算和存储成本。这也克服了灾难性遗忘的问题
PEQA：一种新的量化感知参数高效微调（PEFT）
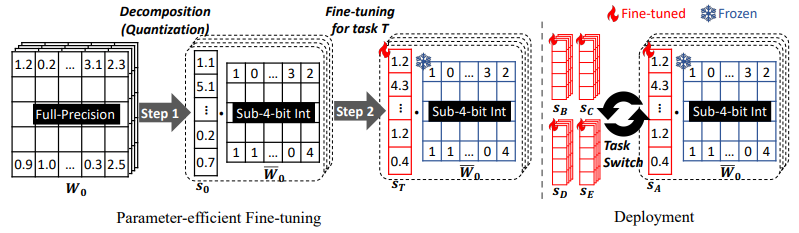
- PEQA 先将每个全连接层的参数矩阵 $W_0$ 分解为低位整数矩阵 $\overline{W}_0$ 和量化向量 $s_0$
- 在微调阶段，PEQA 会针对不同的任务对量化向量 $s_0$（图中红色向量）进行更新
- PEQA 的可训练参数少，内存占用低；在部署阶段依然保持量化结构，实现推理加速
- PEQA 通过多种量化向量切换到不同的下游任务，低位整数矩阵在所有任务中保持共享
QLoRA 引入了新的数据类型 NF4、双重量化和分页优化器等创新概念。这些想法旨在在不影响性能的情况下节省内存。QLoRA 微调 LLaMA-65B 大模型仅需 48G 显存。
4 常见的量化算法
4.1 BnB 拆分异常值 PTQ
背景知识：
- 模型参数中的离群异常值，是导致量化模型性能下降的重要原因
- 尤其是参数量大于 6B 的 transformer 模型，几乎每层都有离群异常值
BnB（也称 LLM.int8 () ）的算法原理：
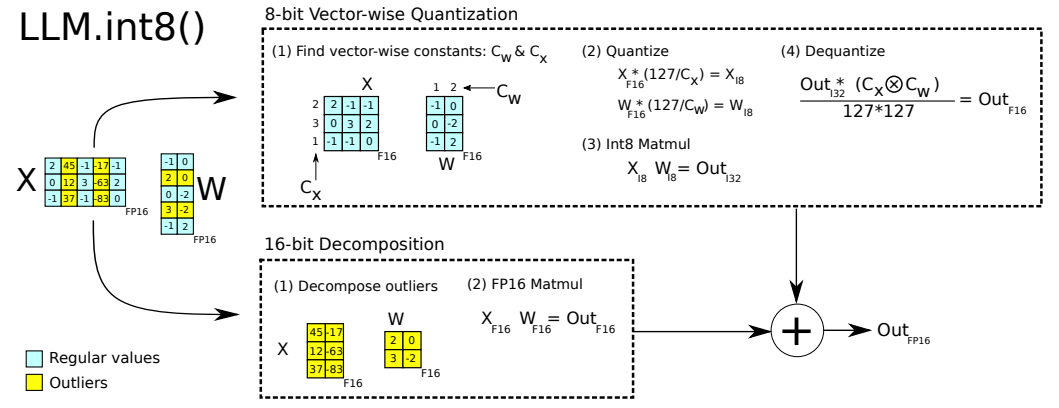
- 主要针对前馈和注意力投影层的矩阵乘法操作，进行量化
- 对于输入的隐含状态，自定义阈值来区分其中的离群异常值
- 对 FP16 离群值矩阵和 Int8 非离群值矩阵分别进行矩阵乘法
- 最后将两种矩阵乘法的结果相加，得到最终的 FP16 结果
非离群参数值会先量化位 Int8 再进行矩阵运算，然后反量化到 FP6
最终效果（原始论文 - 202208）：
- LLM.int8 () 在不降低性能的情况下将推理所需的内存消耗减半
- 3B-T5 模型的推理速度从 312ms/token 降低至 173ms/token
- 11B-T5 模型的推理速度从 45ms/token 降低至 25ms/token
- 在实验中发现，以 6 为阈值区分离群异常值是最佳的
4.2 GPTQ - 4 位非对称 PTQ
前置知识：Hessian 海森矩阵
GPTQ 的发展背景
- OBD （Optimal Brain Damage）是一种经典的模型剪枝方法，OBD 假设不同参数对目标函数的影响是独立的，以此简化目标函数的泰勒展开，并使用 Hessian 矩阵计算参数的"贡献度"来进行神经网络的剪枝
- OBS（Optimal Brain Surgeon）则在 ODB 的基础上去除了独立性假设，并通过计算 Hessian 矩阵的逆直接得到每个参数的重要性排序，然后剪枝
- OBQ（Optimal Brain Quantization）将 OBS 的剪枝思想推广到了模型量化中（量化是对数值的邻近值近似，剪枝可以看作一种将数值近似为 0 的特殊量化），但 OBQ 效率较低（量化一个 GPT3 模型需要耗时数天）
- GPTQ 在 OBQ 的基础上进行改进，在降低量化算法复杂度的同时保留了模型的精度，因而常用于大模型的高效量化（量化一个 176B 的模型耗时 4h）
OBQ 以最小量化误差为目标，先借助 Hessian 矩阵的逆对参数进行重要性排序，然后使用贪心算法顺序量化网络的每一层，并单独计算权重矩阵的每一行
GPTQ 是一种流行的混合量化方法
- 其中模型权重被量化为 int4 类型，而激活值则保留在 float16 类型
- 在推理阶段，模型权重被动态地反量化回 float16 并进行实际的运算
- GPTQ 使用非对称量化方式，由浅到深逐层独立处理每一层的量化
GPTQ 的算法伪代码（原始论文 - 202210）：
- GPTQ 的输入包含当前层的参数矩阵 $W$ 和海森矩阵的逆 $H^{-1}$
- GPTQ 先对参数矩阵进行分块（blocksize=B），然后对块内参数矩阵逐列进行量化；用于量化的误差矩阵 $E$ 会按照重要性加权累积块内的计算量化误差
- 迭代重新分配加权量化误差的量化过程，直到所有值都被量化
顺序量化的计算可视化过程如下：
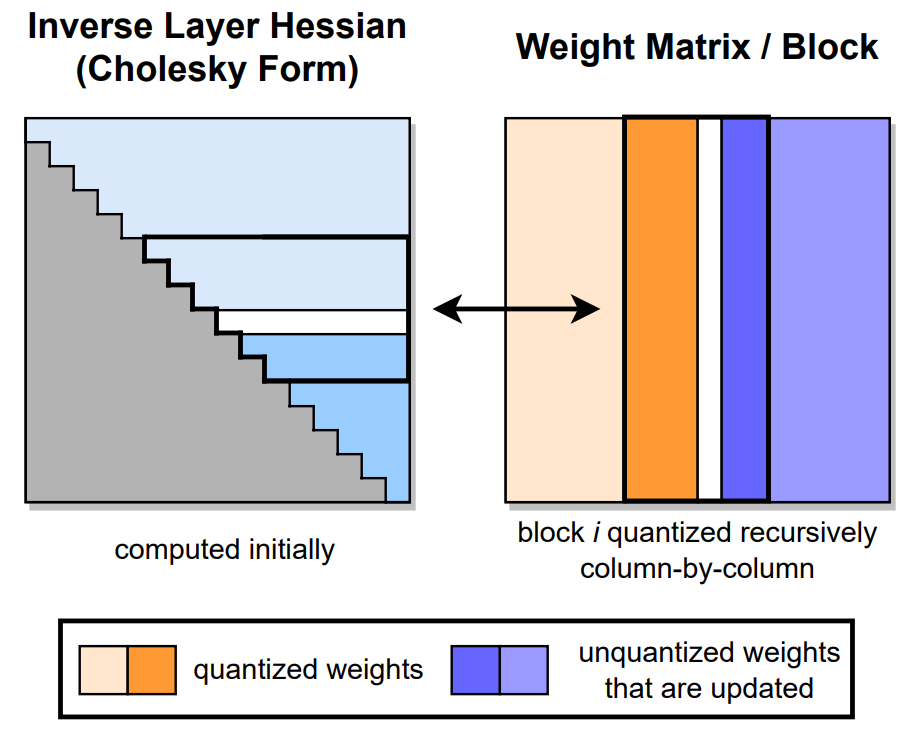
GPTQ 的计算效率优化细节补充：
- 取消贪心算法，顺序量化参数，方便参数矩阵的行并行运算
- 通过参数的延迟更新，缓解带宽压力，大幅提升计算速度
- 用 Cholesky 分解求海森矩阵的逆，通过预先计算增强数值稳定性
4.3 SmoothQuant 平滑激活异常 PTQ
SmoothQuant 是一种兼具准确和性能的 W8A8 量化方法
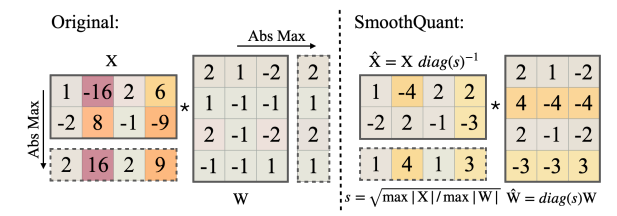
- 由于激活值的量化难度大于模型权重的量化，因此 SmoothQuant 通过数学上等价的逐通道缩放变换，将量化的难度从激活值转移到模型权重上
- 具体来说，SmoothQuant 引入平滑因子 $s$ 来对不同通道下的激活/权重进行缩放：
$$ Y=(Xdiag(s)^{-1})\cdot((diag(s))W)=\hat{X}\hat{W} $$
- 其中第 $j$ 个通道下的 $s$ 定义为：$s_j=max(|X_j|^{\alpha})/max(|W_j|^{1-\alpha})$
- 超参数 $\alpha$ 能平衡模型权重量化和输入激活值量化间的难度，常见取值为 0.5
超参数 $\alpha$ 取值较小时，激活值量化难度大；反之则模型权重量化难度大
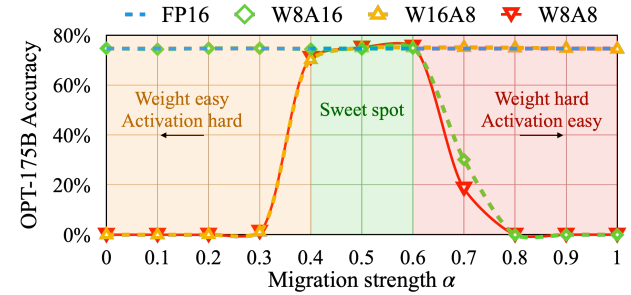
SmoothQuant 其他补充（原始论文 - 202210）
- 对于 GLM-130B 这类激活值异常较多（30%）的情况，$\alpha$ 推荐值为 0.7
- 与 FP16 相比，SmoothQuant 实现了 1.56 倍的推理加速，并且内存占用减半
4.4 AWQ 激活感知权重 PTQ
BnB 量化的思路是按照阈值切分离群值和非离群值，整体进行混合精度训练
AWQ 是一种低比特的 LLM 权重量化方法（原始论文 - 202406）：
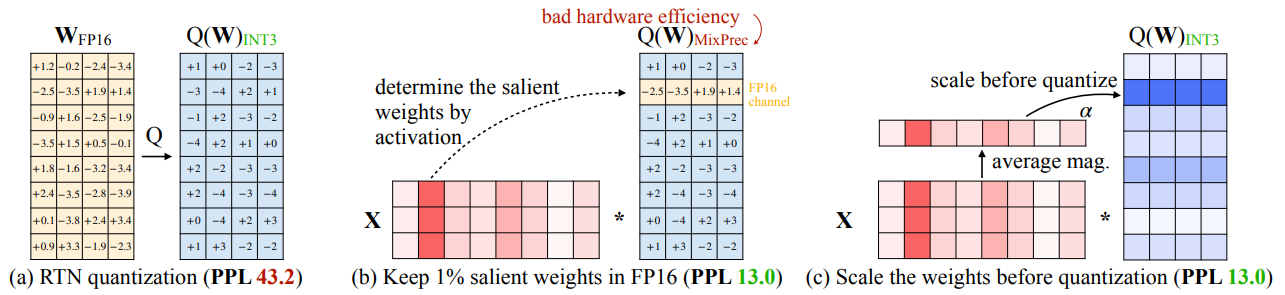
- AWQ 沿用了 BnB 的量化思想，但不再手动设定阈值区分异常值，而是通过激活值（activation）的大小来自动判断相应权重的重要性/显著性
- AWQ 会保留少部分（0.1%-1%）显著权重不进行量化，以减少量化误差；相比于普通的近似值量化（round-to-nearest，RTN），该方式能显著降低困惑度（PPL 43.2 -> 13.0）
- AWQ 引入了新的缩放系数 $s$ 来改善量化的效果，其计算方式如下：
$$ \mathbf{s}^{*}=\arg\min_{\mathbf{s}}\mathcal{L}(\mathbf{s}) $$ $$ \mathcal{L}(\mathbf{s})=|Q(\mathbf{W}\cdot\mathrm{diag}(\mathbf{s}))(\mathrm{diag}(\mathbf{s})^{-\mathbf{1}}\cdot\mathbf{X})-\mathbf{W}\mathbf{X}| $$
- 上式中，$s$ 是缩放系数，$Q$ 是量化函数，$W$ 是量化前的权重矩阵
- $X$ 是来自一个校准数据集的输入，$\mathcal{L}$ 描述了基于缩放系数 $s$ 的量化误差
- 由于函数 $Q$ 不可微，因此 AWQ 定义了搜索空间用于寻找最优的 $s$
AWQ 原理：将权重先放大再进行量化损失的计算可以提高量化的效果
缩放系数 $s$ 的搜索空间定义： $$\mathbf{s}=\mathbf{s_X}^\alpha$$ $$\quad\alpha^*=\underset{\alpha}{\operatorname*{\arg\min}}\mathcal{L}(\mathbf{s_X}^\alpha)$$
- 其中 $s_X$ 是校准数据集的平均激活值，描述了权重的重要性
- 上式将 $s$ 定义为以 $s_X$ 为底数，超参数 $\alpha$ 为指数的固定形式
- 该形式将缩放系数 $s$ 的搜索过程，简化为超参数 $\alpha$ 的搜索过程
4.5 GGUF 适合 CPU 推理的 PTQ
GGML 是一个专注于机器学习的 C 库，该库不仅提供了机器学习的基础元素（如张量），而且还提供了一种独特的二进制格式 GGUF 来分发 LLM
相比于早期的 GGML 格式，GGUF 格式具备更高的灵活性，也能兼容更多的模型结构（GGUF 自 2023 年 8 月份，开始逐步替代 GGML 格式）
GGUF 是一种高效存储大模型的文件格式
- 一个 GGUF 文件包括文件头（文件类型和版本的基本信息）、元数据键值对（模型的额外信息，比如作者、训练信息、模型描述）和张量信息（模型的实际权重和参数）
- GGUF 采用了特殊的二进制编码方式，支持跨平台和跨设备的模型加载运行；兼容多种模型结构，不需要外部库依赖，支持单文件部署
- GGUF 保持生成结果的完整性和可读性，提高传输和存储效率；通过数据压缩和内存映射（mmap）等方式，加快模型的读取和加载速度
- GGUF 兼容多种对模型权重的量化（比如 absmax），因此可能会影响生成文本的质量
GGUF 格式的量化算法更适配于 CPU 推理，而 GPTQ 量化对 GPU 更加友好
使用 llama.cpp 转换 GGUF 格式：
- llama.cpp 是基于 C/C++的 LLMs 推理库，可以将模型转化为 GGUF 格式
- 具体来说，可以使用项目根目录下的
convert_xx.py脚本来一键转换 - 使用
llama-quantize命令即可实现模型的量化，更多可参考官方文档
4.6 BitNet - 1 位量化 QAT
BitNet 使用 BitLinear 层替换了 Trnasformer 中的普通线性层
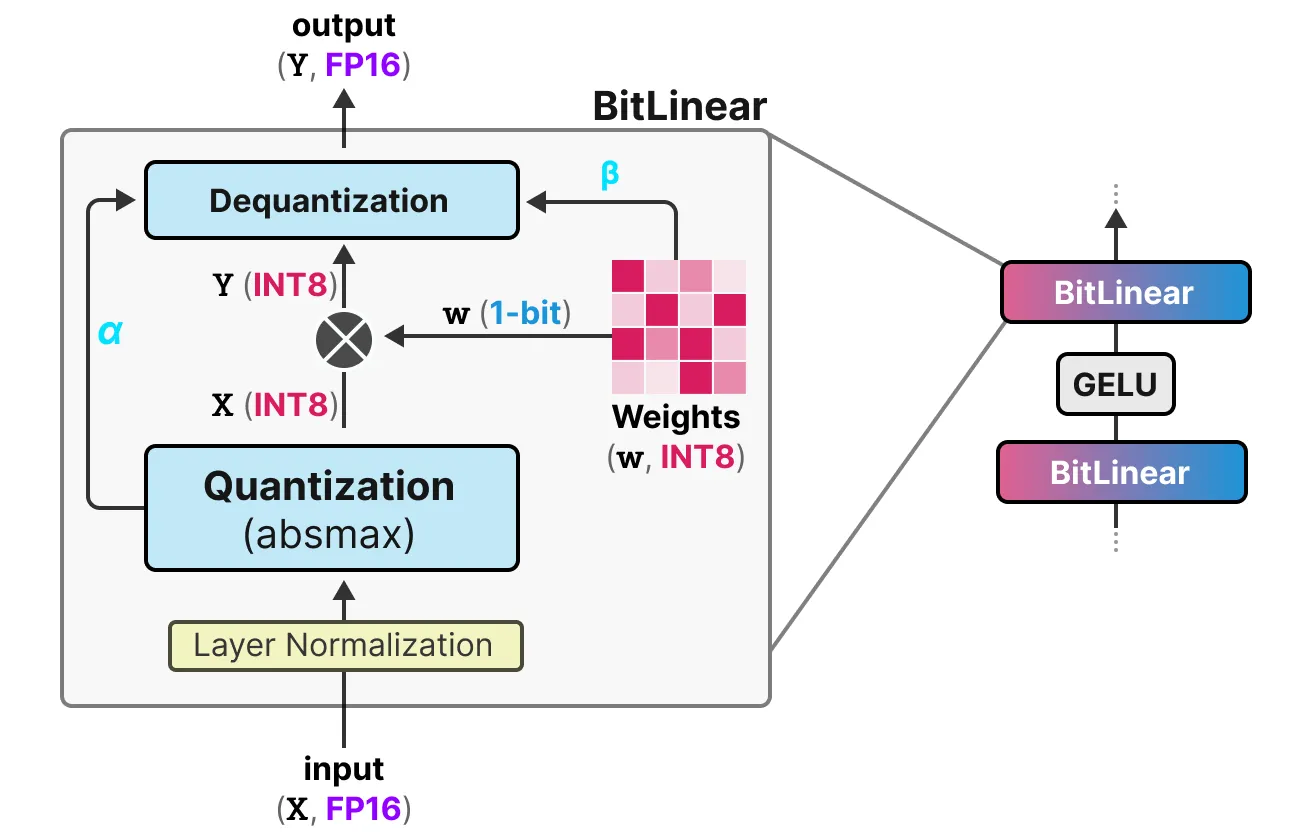
- BitLinear 层使用 1 位表示模型的权重，并使用 INT8 表示激活值
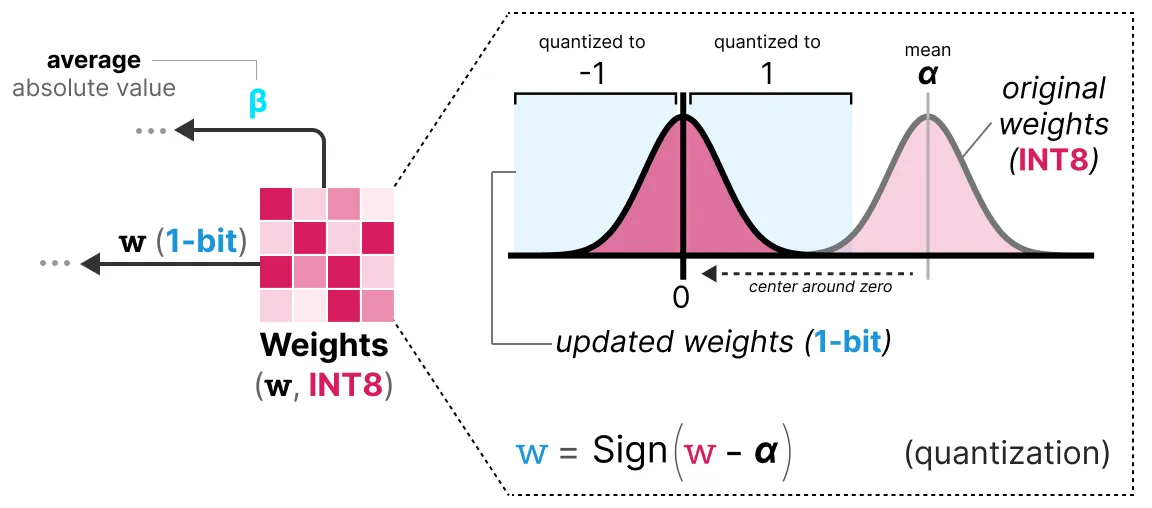
- BitLinear 层会先使用 absmax 算法将激活值进行量化（$X_{FP16} \to X_{INT8}$）；然后针对模型权重进行 1 位量化（$w_{INT8} \to w_{1-bit}$）；最后得到量化输出 $Y_{int8}=w_{1-bit}X_{int8}$
- 量化后，BitLinear 层会跟踪最大激活绝对值 $\alpha$ 和平均权重绝对值 $\beta$ 方便反量化：
$$ Y_{FP16}=Y_{INT8}\cdot \frac{\alpha \cdot \beta}{2^{b-1}} $$
1 位量化：将权重分布移动到以 0 为中心，0 左侧的权重置为 -1，右侧置为 1
BitNet 的其他补充（原始论文 - 202310 ）：
- 随着模型大小的增长，1 位训练和 FP16 训练之间的性能差距变得越小；BitNet 更适合参数量大于 30B 的大模型，对于小模型仍会存在较大的性能损失
- BitNet 的改进版 BitNet1.5b 允许量化权重值为 0（3-bit），此改动可以显著加快计算效率，而且还能起到"特征过滤"的作用（权重值为 0 表示一种忽略）
4.7 其他量化技术简述
HQQ（2023）
- 问题定义：如何在零点量化中取得最优的零点 z 和缩放倍数 s
- 通过对零点量化的公式转换，将其分解为两个子优化问题分别求解
- HQQ 对输入无要求，不需要额外的量化校准数据集（开源代码）
- HQQ 量化 Llama-2-70B 只需不到 5 分钟，比 GPTQ 快 50 倍以上
SpQR（2023-06）
- SpQR 是一种混合稀疏 PTQ，能隔离导致量化误差较大的异常权重值
- SpQR 对异常权重进行高精度存储，对于非异常权重，则分组压缩到 3-4 位
- SpQR 实现了一种基于压缩稀疏行（CSR）格式的稀疏矩阵乘法，加速推理
- 实验结果表明，SpQR在不同模型规模上都能达到小于1%的相对准确性损失
DecoupleQ（2024-04）
- 字节推出的低比特 PTQ 量化（如2-bit）技术，硬件友好，量化误差小
- DecoupleQ 通过将量化问题转化为数学优化问题来提高量化模型的准确性
- 代码开源，但根据网友反馈来看，似乎实际应用还是会有些问题的
5 常见的模型量化库
Bitsandbytes 6k ⭐️：低位量化|LLM. Int8|兼容性好|QLoRA
AutoGPTQ 4.3k ⭐️：基于 GPTQ 算法的模型量化工具包
llm-awq 2.3k ⭐️：AWQ 算法的官方实现，适合学习与复现
AutoAWQ 1.6k ⭐️：4 位 AWQ 量化实现| 3 倍推理加速
参考
A Visual Guide to Quantization
大规模 Transformer 模型 8 比特矩阵乘简介
大模型量化技术原理-LLM.int8()、GPTQ