- 易感者（Susceptible）：存在感染风险的正常人群，用符号$S(t)$来表示
- 感染者（Infective）：已经被感染的人群，用符号$I(t)$ 来表示
- 免疫者（Recovered）：因为隔离/疫苗/病愈等原因而具备免疫力的人群
- 暴露者（Exposed）：指接触过感染者，但暂无感染能力的人群（潜伏期）
1 SI模型
假设与定义：
- 总人口为$N$，不考虑人口的出生与死亡（即总人口不变）
- 不考虑无感染风险的人群，不考虑感染者康复的情况
- 易感者和感染者处于相近的空间内，并且分布均匀
- 用$\beta$表示传染率：感染者接触到易感者后，易感者患病的概率
有的版本的SI模型会使用每个患者在单位时间的平均感染人数$\lambda$，来取代传染率$\beta$。在模型不考虑不同人群之间的隔离情况下，其实$\lambda=\beta I$。即假设每个感染者都能接触并可能导致感染者患病。
由此可知，在从$t$时刻开始的段时间$\Delta t$内，感染者的人数变化可描述如下： $$I(t+\Delta t)=I(t)+\beta \Delta t S(t)I(t)$$ 已知总人口$N$不变，且$N=S+I$。令$\Delta t\to 0$，可得：
$$\frac{dI}{dt} = \beta SI=\beta I(N-I)=\beta NI-\beta I^2$$
SI模型的解析解：
- 上式经过简单公式变换和变量替换后，可转化为一阶线性微分方程
- 一阶线性微分方程可以使用分离变量法进行求解，具体求解过程略
SI类模型的数值解：
- 虽然SI模型具备计算方便且高精度的解析解
- 但是随着模型假设的变化，解析解的计算也逐渐复杂
- 实际应用中，SI类模型多借助第三方工具（Scipy）进行数值求解
SI模型分析：
- 患者增长速度符合发展、爆发、放缓的S型曲线走势
- 由于不存在康复情况，最终感染者人数将趋近于总人口数
- 当$I=N/2$时，感染者的增速最快，对应着疫情爆发的最高峰
- SI模型假设较为理想，是其他传染病模型的基础，实际中使用较少
2 SIS模型
在SI模型基础上，假设与定义有以下调整：
- 感染者可以康复，并存在重复感染的风险
- 假设$\gamma$表示康复率：即感染者恢复健康的概率
此时SIS模型可表示如下： $$\frac{dI}{dt} = \beta SI-\gamma I=(\beta N-\gamma)I(1-\frac{\beta}{\beta N-\gamma} I)$$ SIS模型分析：
- 考虑了康复后，感染者和易感者之间存在相互的转化关系
- 当$\beta N>\gamma$时，将流行病将处于发展期；小于则表明处于消退期
- 当感染与康复出现平衡时，对应的感染人数约为$I_{\ast}=N-\gamma/\beta$
3 基本传染数R0
基于SIS模型的核心要素，就能提取出一个描述病毒传播能力的基本指标$R_0$
基本传染数$R_0$的诞生：
- 定义函数$l(t)$，描述感染者经过时间段$t$之后依然患病的概率
- 由于患者康复概率为$\gamma$，所以$l(t+\Delta t)=l(t)(1-\gamma \Delta t)$
- 令$\Delta t\to 0$，可得：$dl/dt=-\gamma l$，带入初始条件$l(0)=1$可得函数$l(t)=e^{-\gamma t}$
- 在时刻$t$到时刻$t+\Delta t$期间，单个感染者的预期感染人数为$l(t)\times S(t)\beta \Delta t$
- 假设$S(t)=N$，单个感染者的预期累积传染人数$R_0$，可按照以下方式计算： $$\int_0^\infty \beta l(t)Ndt=\beta N\int_0^\infty e^{-\gamma t}dt=\frac{BN}{\gamma}$$
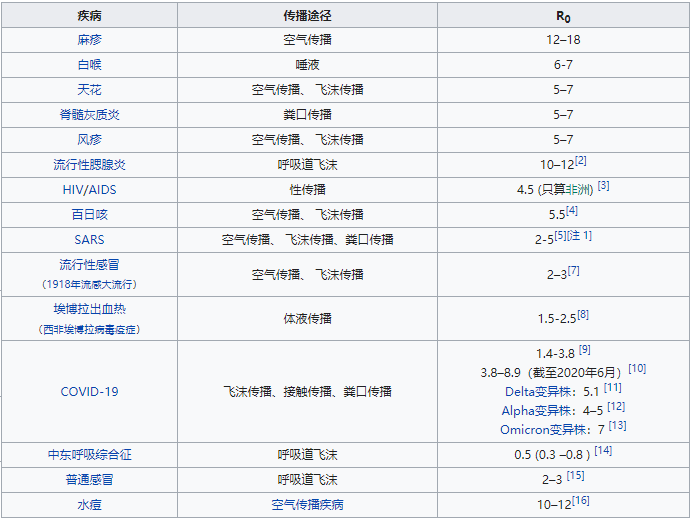
常见疾病的基础传染数（图源：维基百科）：
4 SIR模型
在SIS模型基础上，假设与定义有以下调整：
- 考虑部分人群中具备病毒免疫力，定义为免疫者$R$，区别于易感者
- SIS模型适用于隔离/疫苗/病逾/病逝（？!）等场景产生的免疫能力
- 在本文中，仅考虑病愈这一个场景，方便复用SIS模型中的康复率$\gamma$
- 维持总人口$N$不变的假设，同时存在恒等式$S+I+R=N$
此时SIR模型可表示如下： $$\frac{dS}{dt}=-\beta SI,\ \ \frac{dI}{dt}=\beta SI-\gamma I,\ \ \frac{dR}{dt}=\gamma I$$ SIR模型分析：
- SIR模型无法直接计算解析解，只能进行数值计算
- 由于存在免疫机制，所以感染者的数量将会先增后减，最终趋于0
- 接种疫苗与隔离手段相当于额外干预措施，增加了$R$的绝对数量
寻找群体免疫的临界点
- 假设接种人群占总人口的比例为$p$
- 则基本传染数可修正为有效传播数：$R_0(1-p)$
- 当$R_0(1-p)>1$时，意味着存在传染爆发的风险
- 因此防治疾病的最小接种比例为：$p_{\ast}=1-\frac{1}{R_0}$
5 SIR模型改进
在SIS模型基础上，假设与定义有以下调整：
- 考虑人口的出生与死亡，考虑疾病致死的可能性
- 假设出生率为$b$，疾病致死率为$c$，非疾病致死率为$d$
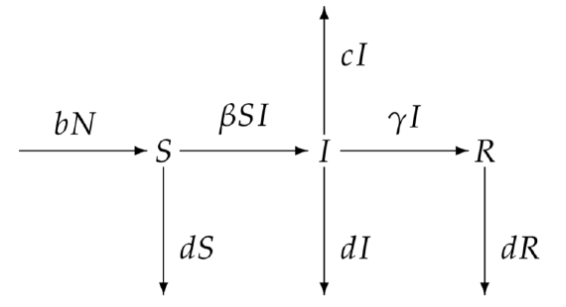
此时修正后的SIR模型可表示如下： $$\frac{dS}{dt}=bN-\beta SI-dS,\ \ \frac{dI}{dt}=\beta SI-(c+d+\gamma) I,\ \ \frac{dR}{dt}=\gamma I -dR$$ 改进版SIR模型分析：
- 引入了更多现实因素的考量，尤其适合针对长期流行病的建模
- 由于新生儿的出现，可能导致原本应该逐渐消退的疾病演变为地方流行病
6 病毒进化方向初探
沿用改进版SIR模型的假设与定义，假设当前病毒类型为A1-1，并且对应流行病处于平衡状态，即$dI/dt=0$，由此可知平衡状态下的感染者人数为$S_{\ast}=(d+c+\gamma)/\beta$
考虑此时病毒出现异种A1-2，对应的感染者数量为$I'(t)$，感染率为$\beta'$，康复率为$\gamma'$，致死率为$c'$。则此时考虑病毒异种的改进版SIR模型可表示如下： $$\begin{equation} \left\{ \begin{gathered} \frac{dS}{dt}=bN-dS-S(\beta I+\beta'I') \ \\ \frac{dI}{dt}=\beta SI-(c+d+\gamma) I \ \\ \frac{dI}{dt}=\beta' SI-(c'+d+\gamma') I' \ \\ \frac{dR}{dt}=\gamma I + \gamma' I' -dR
\end{gathered}
\right.
\end{equation}$$
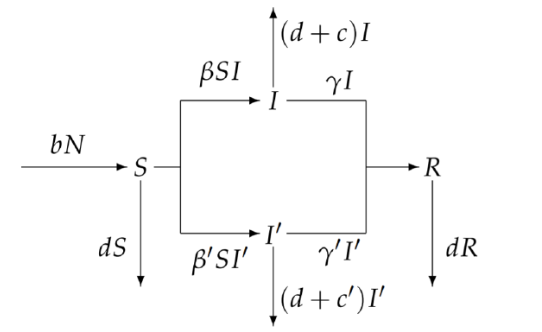
异种病毒感染增长的必要前提是$dI'/dt>0$，带入$S_{\ast}=(d+c+\gamma)/\beta$可得： $$\frac{dI'}{dt}=[\frac{\beta'(d+c+\gamma)}{\beta}-(d+c'+\gamma')]I'>0$$ 化简可知，$I'$要实现指数级增长的必要条件是： $$\frac{\beta'}{(d+c'+\gamma')}>\frac{\beta}{(d+c+\gamma)}$$ 由此可知，病毒的进化方向是更高的$\beta$（感染能力强）和更低的$c,\gamma$（尽量降低疾病的致死率和康复率）。当然此结论也不够严谨，比如没有考虑死人也可以散播病毒的情况~
7 SEIR模型
在SIR模型基础上，假设与定义有以下调整：
- 考虑易感者被传染后暂时不存在传染能力，即病毒存在潜伏期
- 暴露者：处于潜伏期的感染人群，用符号$E(t)$表示
- 发病率：从暴露者转化为感染者的概率，用符号$\delta$表示
此时SEIR模型可表示如下： $$\frac{dS}{dt}=-\beta SI,\ \ \frac{dE}{dt}=\beta SI-\delta E,\ \ \frac{dI}{dt}=\delta E -\gamma I,\ \ \frac{dR}{dt}=\gamma I$$ SEIR模型分析：
- 相比于SIR模型，针对感染者进行了细分，适用于具备潜伏期的流行病
- 发病率和康复率的视角转换：平均潜伏期$=1/\delta$，平均治愈天数$=1/\gamma$
- 具备潜伏期的流行病，一般峰值更低，但是疫情的持续时间会更长
- 本模型未考虑潜伏期具备传染能力的情况，因此针对新冠可能存在乐观估计
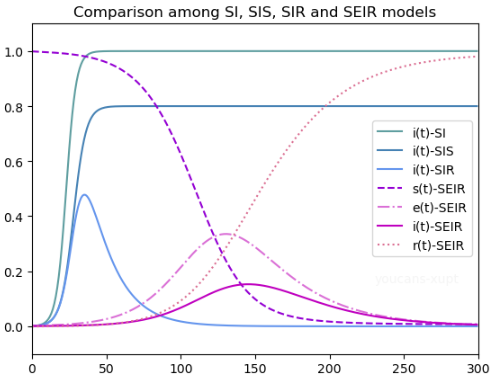（图源：数学建模课-新冠疫情 SEIR模型，图中潜伏期设定为33天）
SEIR模型的改进方向：
- 增加出生、死亡、致死率、病毒变种等因素
- 引入隐形传播者（Undiscovered）：未监测、未隔离的病毒携带者
- 引入易感人群、不易感人群、隔离人群、解除隔离等人群状态
- 考虑潜伏期的传染性、人员流动、人口密度、防控措施等因素的影响
8 SEIRS模型
在SEIR模型基础上，假设与定义有以下调整：
- 患病恢复后获得的免疫力会随着时间的推移而减弱
- 定义免疫群体失去免疫力而再次易感的概率为$\rho$
此时SEIR模型可表示如下： $$\frac{dS}{dt}=-\beta SI+\rho R,\ \ \frac{dE}{dt}=\beta SI-\delta E,\ \ \frac{dI}{dt}=\delta E -\gamma I,\ \ \frac{dR}{dt}=\gamma -\rho RI$$ SEIRS模型分析：
- 最适用于COVID-19的预测，实际建模还会根据年龄/疫苗覆盖率等进行修正
- MSERIS：考虑被动免疫群体M（比如母体抗体促使婴儿产生麻疹免疫）
9 进阶阅读与参考
Mathematics Library-Infectious Disease Modeling